 |
|
Задача 2. 9. Умова “0” варіанта .
Ймовірність виходу зі строю екскаватора упродовж зміни 0,3. На ділянці працює 7 екскаваторів. Яка ймовірність того, що 5 з них пропрацює зміну без аварії.
Розв’язання. Якщо q=0,3; тоp=0,7. тому потрібно знайти, що з 7 екскаваторів 5 пропрацюють без аварії з ймовірністю p=0,7. Застосовуємо формулу Бернуллі ( оскільки n=7, m=5 - невеликі):

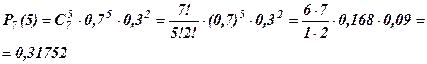

 Відповідь: 0,3175.
Відповідь: 0,3175.
Задача 2. 10. Умова “0” варіанта .
Змінна продуктивність бурового станка розподілена за нормальним законом з параметрами a і σ. На буровій дільниці у кар’єрі працює n станків. Знайти ймовірність того, що змінна продуктивність бурової дільниці не відрізняється від змінного завдання П більше, ніж на ε, якщо a=42, σ =12, n=10, П=380, ε =50.
Розв’язання. 1. Знайдемо математичне сподівання А продуктивності всієї бурової дільниці
( а=42 – це для одного станка), на якій працює 10 станків. За властивістю математичного сподівання
A=M(Y)=M(nX)=n·M(X)=n·a=10·42=420.
2. Тепер знайдемо середнє квадратичне відхилення продуктивності бурової дільниці теж за відповідною властивістю
σ(Y)=  =
= 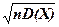 =
=  =
= 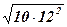
3. Знайдемо ймовірність того, що продуктивність Y бурової дільниці не відрізняється змінного планового завдання П=380 не більше, ніж на ε=50, тобто план може бути перевиконаний або недоконаний не більше, ніж на 50. Позначимо
α=П- ε =380 - 50=330, β=П+ ε=380 + 50=430,
тоді ймовірність знаходиться за формулою:
P(α<Y<β)= 
 =
= 
 =Φ (0,2635)+ Φ (2,3715)=0,1026+0,49 = 0,5926,
=Φ (0,2635)+ Φ (2,3715)=0,1026+0,49 = 0,5926,
де значення функції Φ(x) знайдено по таблиці 2 (див. Додаток)
Відповідь: 0,5926. 
Задача 2. 11. Умова “0” варіанта .
Серед 12 деталей 8 якісних. Вибрали 5 деталей. Знайти:
1) ймовірність того, що серед вибраних деталей 3 неякісні;
2) розподіл випадкової величини X - числа якісних деталей серед вибраних;
M(X), D(X).
Розв’язання.1) 
 ,
,
 ,
,
 .
.
2) Випадкова величина X – число якісних деталей серед вибраних має слідуючі можливі значення: x1=1, x2=2, x3=3, x4=4, x5=5. Ймовірність можливих значень X знайдемо за формулою:  ,
,
 ,
,
 ,
,
 ,
,
 ,
,
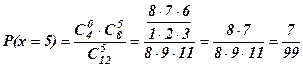 .
. 
Складаємо таблицю розподілу:
| x | |||||
| P(x) | 1/99 | 14/99 | 42/99 | 35/99 | 7/99 |
Перевірка 
3) Знаходимо M(X) і D(X):
M(X) за формулою:


 .
.
Дисперсію знайдемо за формулою:
 ,
,

тоді

Відповідь: 1)  ; 3)
; 3)  ;
;  .
.