Главная | Обратная связь

Формулы различных видов степенных средних величин

Значение К	Наименование средней	Формула средней
простая	взвешенная
-1	Гармоническая		;
	Геометрическая
	Арифметическая
	Квадратическая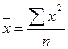

Средняя арифметическая и средняя гармоническаянаиболее распространенные виды средней, получившие широкое применение в плановых расчетах, при расчете общей средней из средних групповых, а также при выявлении взаимосвязи между признаками с помощью группировок. Выбор средней арифметической и средней гармонической определяется характером имеющейся в распоряжении исследователя информации.

Средняя квадратическаяприменяется для расчета среднего квадратического отклонения , являющегося показателем вариации признаков, а также в технике (например, при сооружении трубопроводов).

Средняя геометрическая(простая) используется при вычислении среднего коэффициента роста (темпа) в рядах динамики.

Структурные средние- мода и медиана - в отличие от степенных средних, которые в значительной степени являются абстрактной характеристикой совокупности, выступают как конкретные величины, совпадающие с вполне определенными вариантами совокупности. Это делает их незаменимыми при решении ряда практических задач.

Модойназывается значение признака, которое наиболее часто встречается в совокупности (в статистическом ряду).

Медианойназывается значение признака, которое лежит в середине ранжированного ряда и делит этот ряд на две равные по численности части.

Ранжированный ряд- ряд, расположенный в порядке возрастания или убывания значений признака.

Для определения медианы сначала определяют ее место в ряду, используя формулу

;

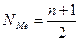где п - число членов ряда.

Если ряд состоит из четного числа членов, то за медиану условно принимают среднюю арифметическую их двух срединных значений.

Применяется мода при экспертных оценках, при определении наиболее ходовых размеров обуви, одежды, что учитывается при планировании их производства. Медиана используется при - статистическом контроле качества продукции и технологического процесса на промышленных предприятиях; при изучении распределения семей по величине дохода и др. Мода и медиана имеют преимущество перед средней арифметической для ряда распределения с открытыми интервалами.