 |
|
Формула размещений с повторениями
Размещения с повторениями можно получить следующим образом. Ячейку из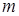 
клеток заполняем, используя 
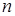различных типов (классов) предметов. Первую клетку можно заполнить 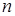способами, вторую - также 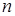способами (поскольку каждый предмет не в единственном числе, а может повторяться сколько угодно раз), третья клетка заполняется также 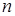способами и т.д. Тогда число размещений с повторениями, обозначаемое 
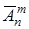, равно
.
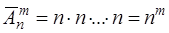Пример. Подсчитаем число четырехзначных автомобильных номеров. Номер составляется из 10 видов цифр. Т.к. в номерах и на первом месте может стоять 0 (в отличие от обычных чисел), то первую цифру можно выбрать 10 способами, вторую – 10 и т.д. и всего номеров будет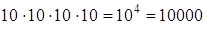 
. (Правда, по неизвестной причине номер 0000 не используется).
Формула сочетаний с повторениями
Сочетания с повторениями образуются так. Имеются объекты 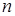различных типов (классов). Выбираем 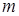предметов, взяв 
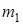предметов первого типа, 
предметов второго типа и т.д. так, что 
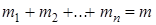. Значения 
могут меняться (от 0 до 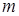), порождая различные наборы. Чтобы подсчитать их число, представим отдельный такой набор в виде ячейки из 
клеток, в которой единицы показывают клетки, занятые объектами различных классов ( 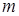штук), а нули — границы между классами или отсутствующие классы ( 
штука):
Различные комбинации будут различаться только положением нулей в ячейке. Т.е. изменение состава выборки связано с различным выбором мест из мест для нулей. Это число равно числу сочетаний из по . Таким образом, число сочетаний с повторениями из 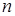по 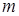, обозначаемое 
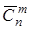равно
.
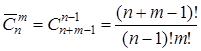Пример. Почетный караул составляется из военнослужащих 5 родов войск и состоит из 12 человек. Сколькими различными способами можно составить команду для почетного караула? В данном случае 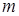= 12, 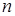= 5 и число возможных способов равно
.
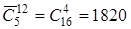