Главная | Обратная связь

МЕТОД КОЭФФИЦИЕНТОВ ДИНАМИЧЕСКОЙ ЖЕСТКОСТИ

Применение этого метода также сопряжено с рассмотрением составной системы из конечного числа упругих балок. К некоторым точкам системы могут быть присоединены жестко или упруго отдельные грузы.

Применяя принцип Д'Аламбера, приложим к каждой массе силы инерции

Для задачи о собственных колебаниях системы можно записать зависимости между перемещениями и силами в виде

(4.2.5)

где k_ji – коэффициент податливости, численно равный перемещению точки с номером j под действием единичной силы в точке i.

Формально система уравнения (4.2.5) может быть преобразована к виду

, (4.2.6)

Где С_ji – коэффициент жесткости, численно равный реакции в точке j, вызванной единичным перемещением точки i.

Системы уравнений (4.2.5) и (4.2.6) удобно записать в матричной форме: 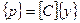, где {y} - матрица-столбец обобщенных перемещений; {р}- матрица–столбец внешних нагрузок; [K] – матрица коэффициентов податливости; [С] – матрица коэффициентов жесткости;

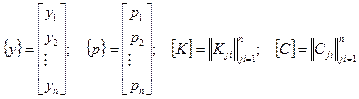
Матрица жесткостей [С] является обратной по отношению к матрице [К], т.е. [К] = [С]^-1 и [C] = [K]^-1.

Дифференциальное уравнение свободных колебаний системы в метричной форме имеет вид: , где [M] - матрица коэффициентов инерции, {у} - матрица-столбец ускорений.

Вместо указанного уравнения можно записать эквивалентное ему уравнение: , где . Исключив врага представления у_i в виде гармонической функции и обозначив x=1/ω², получим или 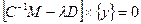,где D - единичная матрица.

Таким образом, мы пришли к частному уравнению.

Следует заметить, что при большом порядке матрицы [С]её может быть связано с потерей точности, поэтому болееоказывается частное уравнение вида .

 

 

4.2.3 Метод ортогональной прогонки

Численными методами легко решаются задачи с начальными условиями (задача Коши). Однако большая часть задач теории упругости носится к другому классу. Это так называемые крайние задачи, решение которых должно быть подчинено граничному условию, сформулированному в различных точках интервала изменения независимой переменной. Краевые задачи можно решать сведением их к задаче Коши. Одним из способов такого решения является метод ортодоксальной прогонки, или дискретной ортогонализации, предложенный С.К. Годуновым в работе [56].

Его сущность заключается в следующем. Разрешающие уравнения краевой задачи, как правило, могут быть легко преобразованы к системе дифференциальных уравнений первого порядка относительно неизвестных. В векторной форме эта система уравнений может быть записана так:

, (4.2.7)

где - вектор искомых функций размерностью n; - матрица переменных коэффициентов размерностью (n×n); b- вектор свободных членов в уравнениях, n - порядок системы уравнений.

Решение уравнения (4.2.7) должно быть подчинено n граничным условием. Будем считать, что m условий сформулировано в начале (α, αn) и 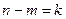в конце интервала интегрирования.

Известно, что общее решение неоднородного линейного уравнения n-го порядка может быть представлено в виде суммы какого-либо решения неоднородного уравнения и линейной комбинации n линейно независимых решений однородного уравнения:

Таким образом, можно записать что .

Векторы и можно найти, решая задачу Коши.

Так как – любое частное решение неоднородного уравнения (4.2.7), то для него можно задать любые начальные условия, в том числе и нулевые:

(4.2.9)

Значение этого вектора в следующей точке определяется численным интегрированием уравнения (4.2.7) при начальных условиях (4.2.9). При выборе начальных условий для векторов являющихся решениями однородного уравнения (4.2.8) [где оно?], надо позабо­титься об их линейной независимости. Проще всего этого добиться, принимая векторы , равными:

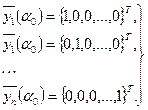
При этом любая пара векторов взаимно ортогональна, что обеспечивает их линейную независимость. Однако выбранные векто­ры должны удовлетворять еще и граничным условиям при любых зна­чениях C_j: .

Выбранные значения векторов на границе интервала интегрирования будут являться начальными условиями для решения задачи Коши на первом подынтервале.

Проинтегрируем на первом подынтервале однородное дифференциальное уравнение (4.2.6) при выбранных начальных условиях, а также решим задачу Коши для неоднородного уравнения (4.2.5) с начальными условиями (4.2.9).

В результате интегрирования получаем решения в точке : 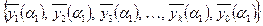. После этого полученные вектора подвергаются ортогонализации и норми­рованию по следующим формулам:

 

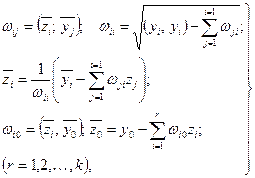(4.2.10)

где - система исходных векторов, подлежащих процессу ортого­нализации и нормирования; z_i - ортонормированные векторы; ω_ij - коэффициенты ортонормирования, которые образуют треугольную матрицу:

В результате проведенной процедуры полученные векторы об­ладают следующими свойствами:

- скалярное произведение любой пары разных векторов равно нулю; т.е. , следовательно, эти векторы ортогональны;

- норма каждого из векторов (i = 1, 2, 3, …, n) равна едини­це: .

Полученные на первом подынтервале векторы принимают за на­чальные значения при решении задачи Коши для однородного урав­нения (4.2.8) на втором подынтервале, а вектор z - для неодно­родного уравнения (4.2.7).

После интегрирования получают вектора: 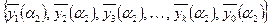, которые снова ортогонализируют и норми­руют по формулам (4.2.10), вычисляя при этом матрицы Z(2) и Ω(2).

Интегрирование заканчивается на последнем подынтервале, в результате чего получается система векторов:

(i = 1, 2, …, k)

Граничные условия при α = α_i позволяют найти к постоянных , входящих в выражение

.

Далее, по рекурентным соотношениям , где можно определить коэффициенты 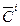для каждого подынтервала интегрирования.

Процесс ортогонализации нормирования решений на каждом подынтервале позволяет избежать потери значащих цифр в результате округления весьма больших и малых величин.

При практическом использовании изложенного метода необходимо помнить, что вычисляемые в процессе ортогонализации скалярные произведения векторов состояния физического смысла не имеют. Поэтому результат ортогонализации существенно зависит от выбора масштабов отдельных компонентов вектора состояния.

 

4.2.4. МЕТОД КОНЕЧНЫХ РАЗНОСТЕЙ

Метод конечных разностей построен на замене производных, входящих в дифференциальные операторы уравнений и краевых условий, описывающих ту или иную физическую задачу, их приближенны­ми выражениями, в которых дифференциалы аргументов и функций заменены конечными приращениями.

Если двухмерную область разбить прямоугольной сеткой с равными шагами hx и hy в каждом из двух взаимно перпендикулярных направлений, то в точке с координатами хт, ут соотношения для первых производных могут быть записаны в виде

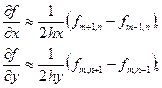(4.2.11)

Здесь символом fi,k [] обозначено значение функции f (x,y) в точке с координатами х_i, у_k.

Для оценки погрешности разностной аппроксимации разложим функцию f (x,y) в окрестности точки х в ряд Тейлора:

(4.2.12)

В выражении (4.2.12) 0(h³x) - остаточный член разложения, имею­щий значение порядка h³x. Подставим это разложение в правую часть первого из соотношений (4.2.11):

,

откуда

(4.2.13)

Величина 0(h²x) в выражении (4.2.13) показывает порядок погреш­ности разностной аппроксимации.

Для аппроксимации производных второго и более высоких порядков, а также для смешанных производных применяются формулы:

(4.2.14)

Погрешность аппроксимации производных в соотношениях (4.2.14) имеет порядок 0(hz).

При аппроксимации граничных условий бывает полезно приме­нять смещенные разности. Например, для аппроксимации граничных условий на контуре области х=0,у могут быть использованы пра­вые разности:

(4.2.15)

на контуре, у - О, х

(4.2.16)

Замена производных в граничных условиях на контуре области производится левыми разностями по формулам:

(4.2.17)

на контуре у = b, х

(4.2.18)

 

Погрешность аппроксимации в формулах (4.2.15)+(4.2.18) .

Поясним сущность применения метода конечных разностей на примере приближенного решения уравнения, описывающего продоль­ные колебания стержня переменного сечения:

(4.2.19)

 

(4.2.20)

 

с граничными условиями U (0, t) = 0; и начальными условиями при

(4.2.21)

 

В уравнении (4.2.20) E - модуль упругости материала стерж­ня; - массовая плотность; F(х) - площадь поперечного сечения стержня; ; - скорость распространения продольной волны в стержне постоянного сечения.

Разделим интервалы (0,1) и (О, Т) точками на М и N равных частей x₀ = 0, х₁ = h, ..., x_m = mh ,..., x_m = l; h = l/M ; t₀ = 0, t₁ = τ,…, t_p=pτ, …, tN=T; τ =T/N. Используя формулы (4.2.11), (4.2.14) получим уравнение в конечных разностях, приближенно заменявшее заданное уравнение (4.2.19):

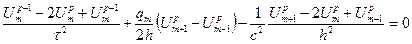(4.2.22)

 

В формуле (4.2.22) верхними индексами, как это принято, обозначены номера точек по временной координате, нижним индек­сом - по пространственной. Уравнение (4.2.22) должно быть вы­полнено во всех точках области (0,l), (0,T).

Приближенная замена граничных условий (4.2.20) может быть осуществлена с использованием смещенных разностей (4.2.17):

(4.2.23)

 

В ряде случаев предпочтительным является метод введения точек, расположенных за контуром рассматриваемой области [57], [58]. Граничные условия (4.2.23) в этом случае могут быть пред­ставлены в виде

(4.2.24)

 

Заметим, что величины перемещений во внутренних точках области m = 0, 1, ..., M на временном слое р+1 вычисляются по известным значениям перемещений, полученным на слоях р и p-1.

Аппроксимация начальных условий (4.2.23) с использованием законтурных точек дает необходимые для начала счета данные

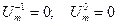(4.2.25)

 

Условия (4.2.25) равносильны предположению о том, что до момен­та начала действия силы (t 0) все точки балки находились в состоянии покоя, тело было недеформировано.

Таким образом, алгоритм решения задачи о продольных коле­баниях стержня переменного сечения методом конечных разностей сводится к следующему:

1) считая начальное состояние невозмущенным, полагаем ; m = 0, 1, …, M (для случая введения законтурной точки m = 0, 1, ..., М+1);

2) по формуле (4.2.22) находим 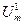во внутренних точках области m = 0, 1, …, M-1 (при введении законтурной точки τ = 0, 1, …, M);

3) значения перемещений на контуре вычисляем по формуле (4.2.23), а для случая введения законтурной точки по формуле (4.2.24);

4) переходим к пункту 2, определяя и т.д.

Аппроксимация исходных дифференциальных уравнений соот­ветствующих начальных и граничных условий является необходимым условием сходимости приближенного вычислительного процесса к точному решению, но недостаточным. Для некоторых разностных схем малые ошибки, допущенные при аппроксимации начальных дан­ных и дифференциальных уравнений, а также наличие неизбежной погрешности, связанной с конечным числом разрядов счета ЭВМ, сильно возрастают при проведении вычислений и делают невозмож­ным получение сколь-нибудь пригодного результата. Это приводит к необходимости исследования устойчивости разностных схем, при­меняемых для решения задач динамики упругих систем.

Одним из наиболее распространенных методов исследования устойчивости разностных схем является гармонический анализ [59], рассматривающий распространение начального возмущения типа гармоники:

, (4.2.26)

 

где - амплитуда гармоники; , - возмущения в начальных данных или в процессе счета (ошибки округления) по х и у соответственно; - круговая частота возмущения; K₁,K₂ - волновые числа.

Для того чтобы гармоника (4.2.26) была решением уравнения (4.2.22), необходимо, чтобы , K₁, K₂ были связаны дисперсионными (или характеристическими) уравнениями. Условие устойчивости разностной схемы формулируется в виде

, (4.2.27)

 

где - корень характеристического уравнения.

Неравенство (4.2.27) означает: если амплитуда каждого гар­монического возмущения возрастает не сильнее, чем , то разностная схема устойчива.

Условие устойчивости разностной схемы налагает ограниче­ние на соотношение шагов по временной и пространственным коор­динатам. Например, в задаче (4.2.19) при qх = 0 условие устой­чивости согласно работе [60] имеет вид: , что физически означает: расстояние, на которое распространяется волна за промежуток времени, равный шагу по времени, не должно превышать шага сетки. Аналогичные условия устойчивости получены для решения задачи об изгибных колебаниях стержня в работе [61]. В работе [62] сформулированы условия устойчивости разностной схемы, применявшейся для решения задачи динамики оболочки с вязкоупругим заполнителем под действием резко изменяющегося внутреннего давления.

Для сложных систем получения априорных оценок устойчивос­ти разностных схем затруднительно. Следует отметить, что распро­страненное в инженерной практике суждения об устойчивости при­меняемых разностных схем, базирующееся на сопоставлении резуль­татов расчета полученных при кратном изменении шага по временя, не всегда обосновано. Так, в работе [72] показано, что при кратном изменении шага по времени может иметь место сходимости разностных решений к результату, не имеющему ничего общего с решением рассматриваемой задачи. Поэтому, в тех случаях, когда априорные оценки устойчивости разностных схем не могут быть получены; целесообразно исследование устойчивости производить путем сопоставления приближенного решения с имеющимся точным для модельных задач.

 

4.2.5. МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ

Одним из методов дискретизации является метод конечных элементов, получивший в последнее время достаточно широкое распространение для решения задач динамики упругих систем. Сущность этого метода заключается в том, что континуальная система разбивается на отдельные элементы, например, при реше­нии плоской задачи - треугольные элементы, работа которых приб­лиженно или точно изучена. Сочленение элементов осуществляется в узловых точках, где полностью удовлетворяются условия равно­весия и неразрывности перемещений. Выполнение условий совмест­ности перемещений в узловых точках обеспечивает непрерывность перемещений и на границах элементов, поскольку предполагается, что перемещения линейно изменяются вдоль любой линии внутри и на границе элемента. Вместе с тем, деформации и напряжения, постоянные внутри каждого элемента, будут различными в каждом из элементов и, следовательно, на границах будут испытывать разрывы.

Наибольшее распространение при решении задач динамики получил вариант МКЭ, соответствующий методу перемещений при реше­нии задач теории упругости. Вариант МКЭ в форме метода перемещений предполагает выполнение следующих основных этапов.

Физическая область задачи делится на подобласти, или конечные элементы;

В рассматриваемой области фиксируется конечное число точек, соответствующих узлам соединения элементов. Предполага­ется, что элементы взаимодействуют между собой лишь в узловых точках. Значения величин перемещений в каждой узловой точке подлежат определению.

Перемещения внутри каждого элемента выражаются через значения узловых перемещений. Для этого перемещения внутри конечного элемента аппроксимируются полиномом, коэффициенты которого определяются с помощью узловых значений перемещений.

Используя принцип возможных перемещений с учетом гео­метрических и физических соотношений, а также формул, связываю­щих перемещения внутри элемента с узловыми перемещениями, полу­чают условия равновесия элемента. При этом предполагается, чти внешние ж упругие силы приложены в узлах.

Представляя полную энергию системы в виде сумму энер­гий, каждая из которых относится к соответствующему элементу, получают уравнение движения конечно-элементной модели рассмат­риваемой системы.

Поясним существо перечисленных этапов на примере получе­ния основных соотношений МКЭ для трехмерного тела. Тело объемом V, ограниченное поверхностью S, разобьем на M элементов объемом .

Занумеруем все узлы: К = 1, 2, …, J. Выразим перемещения внутри каждого элемента через значения узловых перемещений. Для этого вектор перемещений точек, расположенных внутри элемента {u}, задается в виде полиномов по степеням координат x, y, z рассматриваемой точки:

{U} = [А]{α}, (4.2.28)
где [А] - матрица, зависящая от координат элемента; {α} - век­тор коэффициентов полиномиального разложения функции перемеще­ний.

В связи с тем, что количество уравнений, с которыми прихо­дится оперировать в МКЭ, часто весьма велико, общепринято ис­пользовать матричную символику как для сокращения записи, так и для облегчения программирования.

Значения компонентов вектора коэффициентов полиномиально­го разложения {α} выражаются через перемещения и координаты уз­ловых точек.

Например, в случае решения плоской задачи для треугольного элемента с узлами i, j, m разложение вектора перемещений

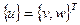(4.2.29)
можно принять в виде

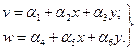(4.2.30)

 

Верхний индекс "Т" в выражении (4.2.29) означает знак транспо­нирования матрицы.

Соотношения (4.2.30), записанные для узловых точек, дают систему уравнений, в результате решения которой определяются значения коэффициентов полиномиального разложения:

откуда

(4.2.31)
где {u}={v_i,w_i,v_j,w_j,v_m,w_m} - вектор узловых перемещений, здесь и далее нижний индекс "k" обозначает номер конечного элемента (k = 1, 2, …, N), [C] - матрица, элементами которой являются комбинации координат узловых точек элемента.

Используя соотношения (4.2.28) и (4.2.31), установим связь между перемещениями внутри элемента и узловыми перемеще­ниями

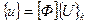, (4.2.32)
где [Ф]=[А][С].

Согласно принципу возможных перемещений, в положении рав­новесия работа внутренних сил равна работе всех внешних сил на возможных перемещениях. Это условие для системы конечных элемен­тов имеет вид:

(4.2.23)
где ; 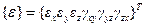– векторы напряжений и деформаций соотв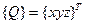етственно; ; векторы объемных и поверхностных сил соответственно.

Напряжения и деформации связаны физическими соотношениями, которые для линейно-упругого тела имеют вид

, (4.2.34)
а связь деформации и перемещений устанавливается геометрически ми соотношениями:

, (4.2.35)
где D - матрица упругих констант, [b] - матрица дифференциаль­ных операторов в геометрических соотношениях.

Получим выражение для деформаций и напряжений внутри ко­нечного элемента через перемещения узловых точек. Уравнение (4.2.35) с учетом соотношения (4.2.32) примет вид

(4.2.36)
где [В]=[b][Ф].

Для вектора напряжений (4.2.34) с учетом соотношения (4.2.36) получим выражение

(4.2.37)

 

Рассмотрим отдельно левую и правую части уравнения (4.2.33). Работа, совершаемая упругими силами внутри k-го элемента, с использованием соотношений (4.2.36) и (4.2.37) мо­жет быть выражена через узловые перемещения и некоторый интег­рал, обозначенный символом

(4.2.38)

 

Матрица [В] называется матрицей жесткости элемента и яв­ляется основной характеристикой системы в МКЭ.

Интегралы по поверхности и объему конечного элемента, со­держащие в правой части равенства (4.2.33) в предположении воздействия на тело из объемных только инерционных сил с уче­том соотношения (4.2.32) можно представить следующим образом:

(4.2.39)
где - матрица приведенных масс элемента; - вектор внешних узловых сил; [ii]k – вектор ускорений узловых точек элемента.

С учетом равенств (4.2.38) и (4.2.39) из соотношения (4.2.33) получим уравнение движения конечного элемента: [M]k[ii]k + [C]k{u}k.

После того как получены матрицы масс [M] жесткости [C]k для каждого элемента k = 1, 2, ..., N можно перейти к рассмотре­нию всей системы конечных элементов.

Матрицы масс и жесткости для системы имеют блочный вид:

 

Уравнение движения конечно-элементной модели рассматривае­мой системы

(4.2.40)
где ; - вектора перемещений и ускорений узловых точек конечно-элементной модели соответст­венно, - вектор приведенных к узлам внешних нагрузок.

Интегрирование уравнения движения конечно-элементной мо­дели (4.2.40) дает возможность получить неизвестные узловые перемещения в виде функций времени. Деформации и напряжения во внутренней области каждого элемента определяются по формулам (4.2.36), (4.2.37). Для численного интегрирования уравнения движения известно большое число шаговых методов, описание ко­торых и сравнительный анализ можно найти, например, в работах [63,73].

 

4.3. ВАРИАЦИОННЫЕ МЕТОДЫ

4.3.1. ОБЩИЕ ЗАМЕЧАНИЯ

Исследование различных явлений в сопротивлении материалов, строительной механике и теории упругости на определенном этапе сводится к решению математических задач, включающих, как прави­ло, дифференциальные уравнения. Эти уравнения описывают поведение некоторой физической модели, аппроксимирующей реальную мо­дель работы конструкции, сооружения, изделия. При этом задают­ся внешние нагрузки, действующие на рассматриваемую конструк­цию, и считаются известными условия ее закрепления.

Таким образом, математически задачи механики деформируемо­го тела представляют собой, в основном, краевые задачи для од­ного или нескольких дифференциальных уравнений с одним или несколькими независимыми переменными.

Точное решение этих краевых задач можно получить лишь в немногих, простых случаях. Большинство же практически важных задач не удается решить точно либо из-за трудоемкости и гро­моздкости выкладок, либо из-за невозможности постановки данной задачи в какой-либо удобной функциональной форме, либо по при­чине трудности удовлетворения граничным условиям, кроме того, могут быть неизвестны функции, являющиеся решениями данных диф­ференциальных уравнений.

В этих случаях на помощь приходят различные методы при­ближенного решения краевых задач. Среди них важное место зани­мают численные методы, в особенности метод конечных разностей и метод конечного элемента, дающие численные значения искомых функций (решений) при тех или иных значениях аргумента. Другую группу приближенных методов решения краевых задач составляют так называемые прямые методы, которые задачи интегрирования дифференциальных или интегральных уравнений сводят к конечным системам алгебраических уравнений. К прямым методам относятся и вариационные, имеющие широкое практическое применение.

Известно, что во многих случаях задачу интегрирования диф­ференциальных уравнений можно заменить задачей об отыскании функций, которые сообщают некоторому интегралу наименьшее зна­чение, т.е. вариационной задачей. Например, при решении крае­вых задач теории упругости вместо интегрирования дифференциаль­ных уравнений можно разыскивать последовательность функций, минимизирующую интеграл энергии. Приближенные прямые методы реше­нная вариационных задач и называются вариационными методами.

Не сопоставляя достоинства и недостатки численных и вариационных методов, отметим, однако, что наличие приближенно­го аналитического решения дает возможность качественного ана­лиза полученного результата; поведение функций, влияние параметров, условия существования, сравнение с некоторыми точными решениями и т.п. Для получения такого приближенного аналитичес­кого выражения искомой функции вариационные методы требуют ре­шения системы одного, двух, трех, редко четырех уравнений; при этом обеспечивается достаточно хорошее приближение.

4.3.2. ВАРИАЦИОННЫЕ УРАВНЕНИЯ ЛАГРАНЖА, КАСТИЛЬЯНО, ГАМИЛЬТОНА

В зависимости от постановки задач теории упругости исполь­зуют различные вариационные принципы механики для получения исходного вариационного энергетического уравнения. Так, при решении статических задач в перемещениях исходят из вариационного принципа Лагранжа, при решении в напряжениях - из принципа Кастильяно, для динамических задач применяется принцип Гамиль­тона.

Выведем вариационные уравнения для общего случая напря­женно деформированного состояния упругого тела. Оно, как из­вестно, описывается системой из 15 уравнений теории упругости, включающей в себя уравнения равновесия, геометрические соотно­шения и соотношения закона Гука. Искомые функции должны удов­летворять определенным граничным условиям.

Точное решение задачи теории упругости определяет некото­рое истинное напряженно-деформированное состояние 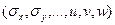рассматриваемого тела. Любое приближенное решение этой задачи определяет близкое, "соседнее" состояние тела 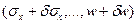, отличающееся от истинного в общем случае, как напря­жениями, так и перемещениями.

Приближение или сравнение "соседнего" состояния с истин­ным возможно двумя способами: во-первых, можно считать, что напряженные состояния одинаковы, а перемещения в этих состоя­ниях различаются между собой на 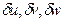(вариации переме­щений); во-вторых, возможен подход, при котором варьируются напряжения при неизменных перемещениях.

Рассмотрим сначала вариационную задачу, основанную на варьировании перемещений.

Как известно, принцип возможных перемещений Лагранжа утверждает, что в положении равновесия при идеальных связях работа всех сил на возможных перемещениях равна нулю. В зада­чах теории упругости под силами подразумевают внутренние напря­жения, компоненты поверхностной (P_x, P_y, P_z) и объемной (X, Y, Z) нагрузок, а в качестве возможных перемещений в рассмат­риваемом случае принимают вариации перемещений.

Таким образом, начало возможных перемещений применительно к упругому телу имеет вид

(4.3.1)
где первый интеграл выражает работу поверхностных сил, второй – работу объемных сил, а третий член – работу внутренних напряже­ний на возможных перемещениях, U₀(u, v, w) – удельная потенциаль­ная энергия деформации упругого тела.

В выражении (4.3.1) компоненты поверхностных и объемных сил считаются постоянными, неварьируемыми величинами. В таком случае, вынося знак вариации за знаки всех интегралов, получим

(4.3.2)

 

Здесь в квадратных скобках представлено выражение полной потен­циальной энергии упругого тела в истинном состоянии. Она скла­дывается из потенциальной энергии U деформации и потенциала П внешней нагрузки. Равенство нулю первой вариации полной энергии означает, что энергия Э в истинном состоянии имеет экстремум. Показывается, что вторая вариация при этом положительна, а значит, потенциальная энергия, соответствующая истинному состоянию равновесия упругого тела, минимальна.

Таким образом, истинными перемещениями (точное решение задачи теории упругости в перемещениях) будут те, при которых полная потенциальная энергия упругого тела приобретает мини­мальное значение. В этом и заключен принцип Лагранжа – принцип минимума для перемещений.

Можно показать, что вариационное уравнение Лагранжа (4.3.2) заключает в себе как уравнения равновесия, так и граничные условия. Следовательно, при решении задачи в перемещениях с ис­пользованием вариационного уравнения Лагранжа нет необходимости в удовлетворении ни уравнений равновесия, ни статических граничных условий - они удовлетворяются автоматически.

Напомним, что рассмотренное вариационное уравнение Лагранжа (4.3.1) получено в результате варьирования перемещений. Существует, как указывалось выше, и другой подход к принципу возможных перемещений, основанный на варьировании напряжений. В этом случае начало возможных перемещений будет записы­ваться в виде

Если объемные силы фиксированы, то , и, вынося знак вариации за знак интеграла, получим

(4.3.3)

 

Уравнение (4.3.3) является вариационным уравнением Кастильяно, которое утверждает, что истинной является та система напряжений, для которой энергия внутренних и поверхностных сил минимальна. Еще раз отметим, что использование уравнения Кастильяно наиболее удобно при решении задачи в напряжениях.

В задачах динамики плодотворными является так называемый вариационный принцип Гамильтона, суть которого состоит в следующем. Если ко внешним силам, действующим на движущееся тело, добавить силы инерции, то согласно началу Д'Аламбера можно рас­сматривать это тело находящимся в состоянии равновесия в любой момент времени.

Таким образом, в принципе возможных перемещений примени­тельно к данному телу необходимо дополнительно учесть работу компонент сил инерции: на соответст­вующих возможных перемещениях 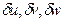, т.е. к выражению (4.3.2) вариации полной потенциальной энергии добавится элемен­тарная работа, представляемая как

.

С учетом этого вариационное уравнение Лагранжа примет вид

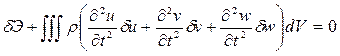
Рассмотрим две траектории движения: истинную и близкую к ней, совпадающую с истинной траекторией толь­ко в граничные моменты временного интервала (t₁, t₂). Други­ми словами, вариации перемещений 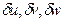, на которые вто­рая траектория отличается от первой, равны нулю в моменты t = t₁ и t = t₂ и в общем случае отличны от нуля при t₁<t<t₂.

Проинтегрировав выражение (4.3.3) по времени в интервале (t₁, t₂) получим

(4.3.4)

 

Интегрирование второго слагаемого выражения (4.3.4) по частям дает:

 

Величина представляет собой кинетическую энергию тела. Таким образом, работа сил инерции на возможных перемещениях в некотором интер­вале времени есть не что иное, как вариация кинетической энер­гии тела в том же временном промежутке.

Теперь соотношение (4.3.4) принимает вид:

Это и есть вариационное уравнение Гамильтона, свидетельствую­щее о том, что именно для действительного движения между момен­тами времени t₁ и t₂ интеграл принимает экстремальное значение. В этом состоит существо принципа Гамильтона или принципа наименьшего действия.

 

4.3.3. ВАРИАЦИОННЫЕ УРАВНЕНИЯ ТЕРМОУПРУГОСТИ

В том случае, когда упругое тело находится в условиях си­лового и теплового нагружения, плотность энергии упругой деформации U₀ теряет свои потенциальные свойства. Если состояние тела описывается параметрами состояния или то потенциалами будут соответственно плотность свободной энергии и плотность термодинамического потенциала Гиббса 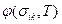. Здесь Т - абсолютная температура; i, k = 1, 2, 3.

Таким образом, при решении статической несвязанной зада­чи термоупругости в перемещениях следует исходить из обобщен­ного вариационного уравнения Лагранжа:

При решении статической несвязанной задачи термоупругости в напряжениях при фиксированных объемных силах необходимо об­ращаться к обобщенному вариационному уравнению Кастидьяно:

В случае малых деформаций и небольшом отклонении текущей температуры Т от начальной Т₀ плотности свободной энергии и термодинамического потенциала Гиббса определяются следующими выражениями [77]:

Изотропный материал

;

где - коэффициенты Ламе, ν - коэффициент Пуассона, - удельная теплоемкость при постоянной деформации, - коэффи­циент линейного расширения, - плотности энтропии, свободной энергии и термодинамического потенциала Гиббса в на­чальном состоянии ;

Анизотропный материал

;

где A_iknm, B_iknm - компоненты тензоров коэффициентов и модулей упругости соответственно, 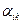- компоненты тензора коэффициентов линейного расширения, - компоненты тензора термических коэффициентов.

В случае малых деформаций изотропного тела при произволь­ном отклонении текущей температуры от начального значения выражения для плотностей свободной энергии и термодинамического потенциала Гиббса согласно работе [77] имеет вид:

;

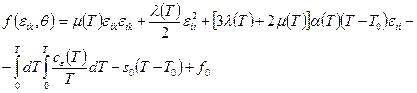где - истинный коэффициент линейного расширения материа­ла.

Био в работе [78] обобщил вариационное уравнение Лагранжа на случай связанной задачи термоупругости при малом отклонении текущей температуры от начального значения. Соответствующее вариационное уравнение записывается следующим образом:

где для изотропного материала 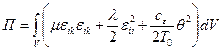- термоупругий потенциал; - функция диссипаций; S_i - векторная функция, определенная соот­ношениями и ; s - плотность энтропии; q_i - компоненты вектора потока тепла: k - коэффициент теплопроводности: n_i - компоненты вектора внутренней нормали к поверхности тела; для анизотропного материала.

,

где n_ij - компоненты тензора термического сопротивления.

В работе Л. И. Балабуха и Л. А. Шаповалова [79] для изотроп­ного тела при малых отклонениях температуры от начального значения дано обобщение вариационного уравнения Био, но при наличии тепловых источников и стоков, что в случае статической задачи сводится к добавлению в выражение термоупругого потенциала слагаемого где q^*- мощность внутреннего источника (стока) тепла.

В последние годы продолжаются исследования в области ва­риационных принципов термоупругости. К их числу относятся работы Э. И. Григолюка с соавторами [80-82]. В работах [81-84] рас­смотрены экстремальные теоремы и вариационные уравнения для статической и динамической связанной термоупругости. Исследо­вания [85-88] посвящены вариационным принципам несвязанной и связанной термоупругости анизотропных тел.

В работе [89] сформулированы вариационные принципы для статической задачи термоупругости физически нелинейной среды, а в работе [90] предложены вариационные принципы для линейной моментной термоупругости.

 

4.3.4. ВАРИАЦИОННЫЙ МЕТОД РИТЦА

В прикладных задачах теории упругости широко используется вариационный метод Ритца, суть которого сводится к следующему.

Пусть необходимо найти функцию w(x), которая дает минимум интегралу

(4.3.5)
при условии на границе Г области .

Ритц предложил приближенное значение w_n искомой функции w искать в виде суммы некоторых, координатных, функций с неизвестными коэффициентами а_i, т.е.

(4.3.6)

 

Функции должны удовлетворять граничным условиям за­дачи как и w_n(x) при любых значениях а_i. Кроме того, систе­ма функций должна быть по возможности полной.

Подставив выражение (4.3.6) в интеграл (4.3.5), получим . Найдем значения коэффициентов а_i, при которых интеграл l будет минимален. Для этого необходимо решить ко­нечную систему алгебраических уравнений:

(4.3.7)

 

Составляя выражение (4.3.6) с найденными коэффициентами a₁, …, a_n получим функцию w_n(x), которую Ритц рекомендует рассматривать как приближенное решение вариационной задачи.

Если w зависит не от одной, а от нескольких независимых переменных, интеграл (4.3.5) будет кратным, а вычислительный процесс развивается аналогично.

В том случае, когда интеграл l является энергетическим для линейных краевых задач, система уравнений (4.3.7) является тоже линейной, построенная минимизирующая последовательность функций w₁, w₂, …, w_n действительно сходится к точному решению w .

Применим вариационный метод Ритца к решению краевых задач теории упругости, основанных на вариационном уравнении Лагранжа т.е. будем искать решение задач статики в перемещениях.

Наиболее удобной формой представления приближенных реше­ний являются частные суммы рядов с неопределенными постоянными коэффициентами. Примем для искомых перемещений следующие выра­жения:

(4.3.8)

 

Функции выбираются в соответствии с рекомен­дациями Ритца, т.е. так, чтобы удовлетворялись граничные условия. В частности, если на границе тела заданы только перемеще­ния u₀, v₀, w₀ то функции должны быть обращаю­щимися в нуль на этой границе.

Вариации перемещений 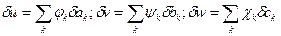; где - вариации произвольных, ничем не связан­ных друг с другом постоянных.

Получим систему алгебраических уравнений для нахождения коэффициентов a_k, b_k, с_k. С этой целью обратимся к вариационному уравнению Лагранжа (4.3.2).

Входящая в это уравнение вариация работы внутренних напряжений может быть записана следующим образом:

.

Подставим теперь это выражение вместе с суммами (4.3.8) в вариационное уравнение (4.3.2):

Поскольку вариации коэффициентов независимы, можно записать

(4.3.9)

 

Легко видеть, что число этих уравнений равно числу неиз­вестных постоянных а_k, b_k, с_k.

Работа U внутренних напряжений представляет собой квадра­тичную форму относительно этих коэффициентов. В самом деле, вариация работы внутренних напряжений в выражении (4.3.2) на ва­риациях перемещений

,

и если подставить сюда выражения напряжений через деформации (соотношения закона Гука), то U окажется квадратичной формой относительно деформаций. Деформации же линейно выражаются че­рез перемещения (геометрические соотношения), а значит линей­но зависят от коэффициентов а_k, b_k, с_k, т.е. действительно представляют собой квадратичную форму относительно этих коэффициентов. В таком случае их первые производные, стоящий и лчйид частях уравнений (4.3.9), представляют собой линейные выражения относительно неизвестных коэффициентов а_k, b_k, с_k.

Заметим, что поскольку объемные и поверхностные силы за­даны, а функции уже выбраны, то правые части этих уравнении являются известными величинами.

Таким образом, соотношения (4.3.9) являются системой ли­нейных алгебраических уравнений для определения произвольных параметров разложения (4.3.8).

Обратим внимание на то, что статические граничные условия в рассматриваемом случае будут удовлетворены автоматически либо точно, либо приближенно, причем тем точнее, чем больше чле­нов ряда взято в разложении (4.3.8). Так как выбор функции заранее удовлетворяющих граничным условиям в напряже­ниях, часто является трудным, то это обстоятельство дает пре­имущества методу Ритца.

 

4.3.5. О ДРУГИХ ВАРИАЦИОННЫХ МЕТОДАХ

Л. В. Канторовичем был предложен прямой вариационный метод, применимый к функционалам, зависящим от функций нескольких не­зависимых переменных. Согласно этому методу приближенное реше­ние вариационной задачи имеется в виде:

(4.3.10)
но коэффициенты a_i(x_k) не постоянные, как в методе Ритца, а представляют собой неизвестные функции одной из независимых переменных х_k. В этом случае интеграл I_n (приближение интегра­ла I) оказывается функционалом: , зависящим от n функций переменной х_k. Функции a_i(x_k) выбирают­ся аналогично константам а_i - в методе Ритца, а именно: из ус­ловий экстремума исходного функционала I_n.

Если ограничиться в сумме (4.3.10) n членами, то получим приближенное решение, причем более точное, чем по методу Ритца с теми же координатными функциями при том же значении n. Большая точность объясняется тем, что класс функций 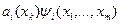значительно шире класса функций поэтому среди более широкого класса функций легче выбрать те, которые будут аппроксимировать точное решение с меньшими погрешностя­ми.

В последнее время благодаря трудам советских математиков применяется конечно-разностный метод Эйлера для решения вариационных задач, сущность которого заключается в том, что значе­ния функционала (4.3.7) рассматриваются на отрезках прямых, представляющих n звеньев ломаной - приближенного решения. При этом задаются абсциссы граничных точек звеньев, и функционал (4.3.7) становится функцией ординат граничных то­чек ломаной линии. Эти ординаты определяются, из условия экстре­мума этой функции, т.е. из системы уравнений:

Если увеличивать число разбиений n, то в пределе можно полу­чить точное решение задачи.

В заключение этого раздела отметим, что помимо описанных выше вариационных методов существуют и другие. Для знакомства с ними можно рекомендовать обстоятельные работы [75,76], в ко­торых, кроме того, дано обоснование рассмотренным здесь мето­дам.

 

4.4. МЕТОД БУБНОВА-ГАЛЕРКИНА

К методу Ритца тесно примыкает приближенный метод решений дифференциальных уравнений, разработанный И. Г. Бубновым и Е. Г. Галеркиным. Этот метод не является вариационным, но относится к прямым методам решения краевых задач. Процедура этого метода часто приводит к тем же операциям, что и метод Ритца. Он удобен и при решении нелинейных задач.

, (4.4.1)
где L - заданный дифференциальный оператор.

Как и ранее, решение ищется в, виде конечной суммы

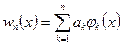, (4.4.2)
причем функции должны удовлетворять граничным условиям задачи и.составлять полную систему.

Если w(х) является точным решением задачи (4.4.1), то оче­видно,

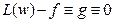
и в этом случае функция g, тождественно равная нулю, ортого­нальна ко всем функциям , т.е.

Если в качестве решения задачи (4.4.1) взять приближенное (4.4.2), то . Ясно, что значение "ошибки" зависит от выбора коэффициентов. И. Г. Бубнов и Б. Г. Галеркин предложили оп­ределять коэффициенты а_k, при которых эта "ошибка" минимальна из условия ортогональности ее ко всем функциям 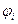, т.е. из уравнений

или (4.4.3)

 

В этом случае при достаточно большом числе n членов суммы (4.4.2) приближенное решение будет весьма мало отличаться от точного.

Подставив сумму (4.4.2) в выражение (4.4.3), получим

Введя функции , предыдущее равенство запишется в виде:

Потребуем, чтобы функции были ортогональны друг к другу вместе со своими производными. Тогда в сумме останется лишь член, у которого k = i, что и даст возможность определить коэффициент из уравнения .

Заметим, что при переменных коэффициентах дифференциаль­ного оператора L требуется ортогональность функций с соответствующим весом.

Сходимость метода Бубнова-Галеркина доказана для интег­ральных уравнений типа Фредгольма и для обыкновенных дифференциальных уравнений с вполне непрерывным оператором при одно­значности решения. Более подробные сведения по вопросу о схо­димости метода содержатся в работе [75].

Метод Бубнова-Галеркина успешно применяется как для реше­ния статических и динамических задач в перемещениях, так и для приближенного определения критических нагрузок или частот собственных колебаний упругих систем. В этом случае задача сво­дится к отысканию собственных значений определителя алгебраи­ческой системы (4.4.3).

Достоинством метода Бубнова-Галеркина является то, что путем подходящего подбора аппроксимирующих функций можно значительно ускорить сходимость приближенного решения. Это позво­ляет инженеру активно вмешиваться в порядок вычислений, применяя свой производственный опыт и техническую смекалку. "Следу­ет учесть, - пишет Х. М. Муштари в предисловии монографии И. В. Свирского, - что усложнение программирования при использовании мето­да Бубнова-Галеркина вознаграждается тем, что можно сразу полу­чить хорошо обусловленную систему уравнений путем подходящего подбора аппроксимирующих функций. Эту систему при большом чис­ле неизвестных значительно легче решать, чем системы, полученные другими способами, при этом удается избежать накопления ошибок от округления чисел" [54].

Особенно наглядно проявляются преимущества этого метода при решении пространственных задач динамики упругих систем, когда искомые функции описываются сложной исходной системой дифференциальных уравнений. Применение матричных методов здесь бывает сопряжено со столь большими системами уравнений, что их трудно решать даже с помощью современных ЭВМ.

Между тем, использование для этих задач метода Бубнова-Галеркина приносит часто практически ценные результаты.

Покажем применение метода Бубнова-Галеркина в статической задаче теории упругости в перемещениях.

Исходная система дифференциальных уравнений равновесия уравнения Ламе - имеют вид:

(4.4.4)

 

Приближенное решение этой системы будем искать в виде:

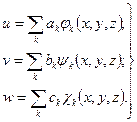(4.4.5)

 

Функции должны удовлетворять соответ­ствующим статическим и кинематическим граничным условиям зада­чи и представлять полные системы ортогональных функций.

В соответствии с процедурой метода Бубнова-Галеркина будем иметь:

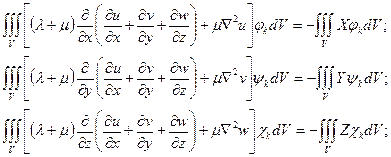
Правые части этих уравнений представляют собой известные величины. Таким образом, и в этом случае получили систему линейных алгебраических уравнений относительно искомых коэффици­ентов а_k, b_k, с_k, причем число уравнений равно количеству коэффициентов.

Метод Бубнова-Галеркина дает в сравнении с методом Ритца значительные упрощения вычислений в тех случаях, когда возможно удовлетворение статических граничных условий.

 

4.5. МЕТОД ТРЕФТЦА

Если в методах Ритца и Бубнова-Галеркина искомые функции должны обязательно удовлетворять граничным условиям, но не диф­ференциальным уравнениям задачи, то в методе Трефтца приближенное решение точно удовлетворяет дифференциальным уравнениям, но не удовлетворяет, вообще говоря, граничным условиям рассматри­ваемой задачи. Другими словами, в методе Трефтца применительно к задачам теории упругости функци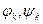и и ⇐ Предыдущая12