ОПИСАНИЕ ЛАБОРАТОРНОГО СТЕНДА

Лабораторный стенд представляет собой электрическую схему, состоящую из резисторов, конденсаторов, индуктивностей, имитирующих активные и реактивные сопротивления линии электропередачи и нагрузки. В качестве активных сопротивлений линий электропередачи выбраны низкоомные резисторы, позволяющие изменять сопротивления линий. В схему включены выключатели SB2, SB3, SB4, позволяющий, образовывать разомкнутые электрические сети, кольцевые сети, сети с двумя номинальными напряжениями, имитировать аварийные ситуации в электрических сетях.

В электрической схеме предусмотрены гнезда и перемычки P1 ... P5, позволяющие изменять конфигурацию сети, а также включать электроизмерительные приборы.

Сигнальные лампы HL1 и HL2 служат для контроля наличия напряжения. Схема имеет батарею конденсаторов С_К, служащих для компенсации реактивной составляющей сетей.

Электрическая схема стенда собрана на плате и расположена внутри стенда. На лицевой панели лабораторного стенда выполнена мнемосхема. Вместо изображения выключателей, клемм, сигнальных ламп на панель выводятся сами выключатели, клеммы и сигнальные лампы.

В качестве электроизмерительных приборов в лабораторной работе используются многопредельные комбинированные приборы (аналоговые и цифровые) – тестеры.

3 ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

1Выполнить расчет режима электрической сети с двумя номинальными напряжениями со следующими исходными данными:

S₄ = 1 + j 0,47 ВА

z₁₂= 0,48 + j 0,45 Ом

z₃₄= 4,9 + j 2,5 Ом

в_С₃₄ = wC₃₄; C₃₄ = 0,1 мкФ

в_С₁₂ = wC₁₂; C₁₂ = 0,25 мкФ

U_{1 НОМ} измерить с помощью многопредельного комбинированного прибора

DР_Т + jDQ_T = 0,036 + j ,034 ВА

U_{3 НОМ} = U_{2 НОМ}/К_Т;

где К_Т = 5,2

r_Т = 0,5 Ом - активное сопротивление трансформатора

х_Т = 1 Ом - реактивное сопротивление трансформатора.

2 Измерить на лабораторном стенде (после сборки соответствующей схемы) и определить DS₃₄, S₄, S₃, DS₁₂, S₁ DU₁₂ , DU_34, U_2, U_3, U₄.

3 Вычислить абсолютные расхождения между расчетными и практически измеренными значениями величин. Объяснить причину расхождения.

4 Составить баланс мощностей для исследуемой схемы.

Примечание: падение напряжений DU₁₂ , DU₃₄определяется как сумма падений напряжений на обоих проводах линии.

4 МЕТРОЛОГИЧЕСКАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ

Результаты измерений можно представить в следующем виде:

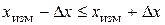, (23)

где ∆x – погрешность измерений.

Точно определить величину погрешности невозможно, так как она носит случайный характер. Иначе можно было бы найденную погрешность ввести в результат измерения и получить истинное значение x_ист. Задачей математической статистики является наилучшая оценка результата x_ист и нахождение пределов интервала (23) по результатам измерений.

Если проведено n измерений величины x, то среднее арифметическое значение принимается за лучшую оценку истинного результата измерений

, (24)

где x_i – результат i-го измерения.

Средняя квадратичная погрешность определяется по формуле

, (25)

где n – число измерений.

Важно знать, насколько может отличаться от истинного значения x среднее арифметическое, полученное по формуле (24) для n повторных равноточных измерений. Из теории видно, что средняя квадратичная погрешность среднего арифметического S равна средней квадратичной погрешности каждого результата измерений S_n, деленного на корень из числа измерений n

. (26)

Вероятность того, что результат измерений отличается от истинного на величину, не большую, чем ∆x обозначим через α. Вероятность α называется доверительной вероятностью, а интервал значений измеряемой величины от -∆x до +∆x называется доверительным интервалом.

Определим доверительный интервал. Чем большим он будет установлен, тем более вероятно, что x_ист окажется в этом интервале. Но широкий интервал дает меньшее представление относительно величины x_ист. При учете только случайных погрешностей и при небольшом числе измерений n для уровня доверительной вероятности α полуширина доверительного интервала равна

, (27)

где t_α_,_n – коэффициент Стьюдента.

Для окончательной установки границы доверительного интервала необходимо расширить его с учетом систематической погрешности ∆x_сист. Систематическая погрешность, как правило, указана в паспорте или на шкале прибора, а в некоторых случаях может быть принята равной половине цены деления младшего разряда шкалы. Суммарная погрешность определяется как корень квадратный из суммы квадратов случайной и систематической погрешностей:

. (28)

Таблица 1 – Коэффициент Стьюдента

α = 0,68	α = 0,95	α = 0,99
n	t_α,n	n	t_α,n	n	t_α,n
	2,0		12,7		63,7
	1,3		4,3		9,9
	1,3		3,2		5,8
	1,2		2,8		4,6
	1,2		2,6		4,0
	1,1		2,4		3,7
	1,1		2,4		3,5
	1,1		2,3		3,4
	1,1		2,3		3,3

Определенная по формуле (28) величина ∆x является абсолютной погрешностью.

Относительная погрешность определяется как

, (29)

и выражается в процентах. Выражение (29) позволяет оценить величину погрешности по отношению к самой измеряемой величине.

При обработке результатов прямых измерений предлагается следующий порядок операций.

1 Вычисляется среднее значение из n измерений по формуле 24.

2 По формуле 25 определяется среднеквадратичная погрешность среднего арифметического значения.

3 Задается доверительная вероятность α и определяется коэффициент Стьюдента t_α_,_n для заданного α и числа произведенных измерений n по таблице 1.

4 По формуле 27 находится полуширина доверительного интервала (абсолютная погрешность результата измерений).

5 Оценивается относительная погрешность результата измерений по формуле 28.

6 Окончательный результат записывается в виде

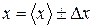. (30)

КОНТРОЛЬНЫЕ ВОПРОСЫ

1 Какие величины требуется определить на первом этапе расчета (последовательность и формулы)?

⇐ Предыдущая 12