Главная | Обратная связь

Теоретические сведения

Модульная арифметика

Простейшей задачей целочисленной арифметики является определение того, делится ли одно число на другое без остатка. Это выясняется, например, делением "в столбик". Если получен остаток 0, то можно сделать заключение о делимости. Если требуется проверка результата, то необходимо умножить частное на делитель и убедиться, что результат равен делимому.

Говорят, что число а делится на число 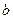(или что а кратно 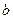), если можно подобрать такое число с, чтобы выполнялось равенство .

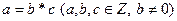Помимо делимости возможен вариант деления с остатком. Для натуральных а и b (делимого и делителя) единственным образом находятся числа q и r (частное и остаток), обладающие следующими свойствами: 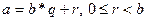. Число называют вычетом числа а по модулю числа 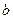. Записывают следующим образом: или просто 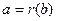. Читается это так: «число а сравнимо с числом r по модулю b». В языках программирования имеются операции для нахождения частного и остатка от деления целых чисел. Условие 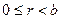говорит о том, что остаток всегда неотрицателен и меньше делителя. При получается определение делимости чисел.

Примеры: 853=20*43+13 => 853=13(mod 20), 8=1(mod 7), 5=0(mod 5), 2= 2(mod 5).

Шифр Цезаря

Простейшим применением модульной арифметики в практической криптографии является шифр Цезаря.

Будем считать, что все шифруемые числа неотрицательны и по величине меньше некоторого заданного числа т. Тем же условиям будут удовлетворять числа, полученные в результате шифрования. Это позволяет считать, что числа являются элементами кольца вычетов 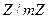. Шифрующая функция при этом может рассматриваться как взаимооднозначное отображение колец вычетов: .

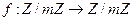Число 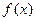представляет собой сообщение 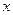взашифрованном виде.

Простейший шифр такого рода – шифр замены – соответствует отображению 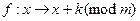при фиксированном целом 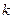. Подобный шифр использовал еще Юлий Цезарь. В шифре Цезаря т – размерность алфавита; k – сдвиг (в шифре Цезаря k = 3).

Алгоритм Евклида

Одна из часто встречающихся задач (не только в математике, но и в криптографии) состоит в том, чтобы узнать, имеет ли данный набор чисел общий делитель, отличный от 1 (как говорят, нетривиальный делитель, так как 1 является делителем любого набора чисел). Числа, которые не имеют нетривиального общего делителя, называются взаимно простыми.

Обычно сразу ищут наибольший общий делитель (НОД), который делится на все остальные делители и, таким образом, содержит их «в себе».

Например, набор чисел 72, 84, 132, 144 имеет общие делители 2, 3, 4, 6, 12. Наибольший общий делитель равен 12 (пишется НОД = 12). Он делится на все общие делители. Известно решение задачи поиска НОД через разложение каждого из чисел на простые множители. Этот алгоритм становится неприемлемым при увеличении разрядности чисел. Например, число больше миллиарда, тогда для разложения его на простые множители потребуется таблица первых сотен или тысяч простых чисел, а построение этой таблицы – задача более трудоемкая, чем исходная. Кроме того, хранение таблицы простых чисел потребует ресурсных затрат. Следовательно, данный метод неприменим в компьютерных вычислениях.

Существует очень простой и эффективный метод нахождения наибольшего общего делителя. Это так называемый алгоритм Евклида с вычитанием. Из набора выбираются любые два ненулевых числа, и большее из них (или любое, если числа равны) заменяется разностью этих чисел. Этот процесс повторяется до тех пор, пока не останется одно ненулевое число. Это число и будет наибольшим общим делителем исходного набора, состоящего из натуральных чисел.

Выбирая для вычитания различные пары, можно получить разные алгоритмы. Все эти алгоритмы будут решать поставленную задачу. Для того чтобы в этом убедиться, необходимо обосновать корректность алгоритмов, т.е. доказать, что каждый такой алгоритм обязательно закончит свою работу, и что полученный в результате работы алгоритма набор будет содержать только одно ненулевое число и что это число будет наибольшим общим делителем исходного набора. Корректность изложенного метода доказывается с помощью двух утверждений: если числа и делятся на 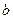, то и их разность делится на 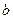, и числа набора остаются неотрицательными. Наконец, процесс изменения набора обязательно закончится, так как после каждого вычитания сумма чисел набора уменьшается. В то же время эта сумма всегда есть положительное целое число, следовательно, процесс не может длиться бесконечно (очевидно, что число шагов не превышает суммы чисел исходного набора).

Простые и составные числа

Одной из задач, возникающих при применении криптометодов, является задача определения того, является ли число простым или составным. Существует достаточно эффективный способ убедиться в этом, не разлагая число на множители. Согласно малой теореме Ферма, если число N простое, то для любого целого а, не делящегося на N, выполняется сравнение 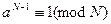. Если при каком-то а сравнение нарушается, можно утверждать, что N – составное. Проверка не требует больших вычислений. Вопрос только в том, как найти для составного N целое число а, не удовлетворяющее сравнению 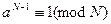. Можно попробовать применить полный перебор на отрезке (1; N). Но такой подход не всегда дает то, что хотелось бы. Имеются составные числа N, обладающие указанным свойством для любого целого а с условием НОД(а, N) =1. Такие числа называются числами Кармайкла.

В 1976 г. Миллер предложил проверку иного условия. Если N – простое число, , где t нечетно, то, согласно малой теореме Ферма, для каждого а с условием НОД(я, N) = 1 хотя бы одна из скобок в произведении делится на N. Обращение этого свойства можно использовать, чтобы отличить составные числа от простых.

Пусть – нечетное составное число, 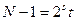, где t нечетно. Назовем целое число 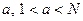, «хорошим» для N, если нарушается одно из двух условий:

а) не делится на ;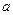

б) или существует целое , такое что .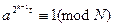

Из изложенного ранее следует, что для простого не существует «хороших» чисел а. Если же N составное, то, как доказал Рабин, их существует не менее 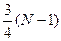. Теперь можно построить вероятностный алгоритм, отличающий составные числа от простых.

1. Выберем случайным образом 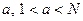, и проверим для него указанные свойства а) и б).

2. Если хотя бы одно из них нарушается, то число N – составное.

3. Если выполнены оба условия а) и б), возвращаемся к шагу 1. Составное число не будет определено как составное после однократного выполнения шагов 1–3 с вероятностью, не большей 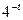. А вероятность не определить его после k повторений не превосходит 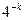, т.е. убывает очень быстро.

Поиск обратного по модулю числа

Для каждого целого числа с и положительного числа d найдется единственная пара целых чисел Q (частное) и s (остаток) таких, что 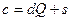, где . Частное обозначается как .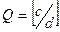

Для нахождения наибольшего общего делителя двух заданных положительных чисел и 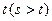применяется алгоритм Евклида, который сводится к последовательности шагов

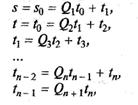
где остановка наступает при получении нулевого остатка. Последний ненулевой остаток 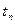равен наибольшему общему делителю. В матричном виде шаги алгоритма Евклида выглядят так:

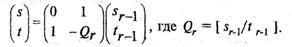
Таким образом, если 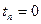, то

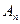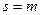Число d, обратное по модулю т числу е (т. е. ed = l(mod m)), является элементом матрицы , где , a 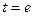.