Главная | Обратная связь

Алгоритм шифрования с открытым ключом RSA

Кольцо вычетов по модулю составного числа и его мультипликативная группа

Кольцо вычетов 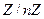, где число 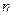равно произведению двух больших простых чисел 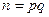, является коммутативным кольцом с единицей. Мультипликативная группа этого кольца является абелевой и циклической и состоит из ненулевых чисел, меньших 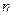и взаимно простых с 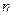. Остатки от деления образующей группы на и 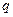равны, соответственно, образующим мультипликативных групп поле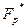й и . Поэтому образующая группы может быть найдена по китайской теореме об остатках. Порядок группы равен значению функции Эйлера от 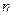: . По определению порядка группы для любого элемента 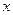группы имеет место равенство .

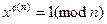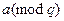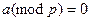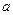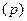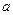Любой элемент кольца может быть единственным образом представлен в виде и и обратно по китайской теореме об остатках. Если , то при надлежит идеалу и не является элементом группы , при этом элемент образует в мультипликативную группу, изоморфную . Единичным элементом в этой группе является элемент, сравнимый с 1 по модулю q и сравнимый с нулем по модулю р.

Сложность нахождения порядка группы полиномиально эквивалентна сложности разложения числа .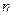

Алгоритмы шифрования и дешифрования

RSA является криптосистемой с открытым ключом. Ключ содержит две составляющие: открытую, которую можно публиковать, и секретную. Открытый ключ содержит число 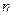и показатель шифрования 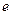. Секретный ключ содержит показатель дешифрования 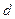. Показатели шифрования и дешифрования связаны между собой равенством .

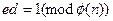Любой блок текста 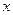, представленный числом, меньшим 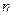и взаимно простым с 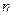, может быть зашифрован любым пользователем с помощью опубликованного ключа: . Дешифрование криптограммы 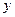может быть осуществлено только владельцем секретного ключа : .

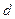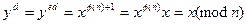Алгоритм цифровой подписи

Цифровая подпись выполняется аналогично шифрованию и дешифрованию. Ключ создания подписи является конфиденциальной информацией данного пользователя и содержит показатель 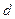. Соответствующий ему ключ проверки подписи содержит число 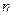и показатель 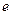. Этот ключ является общедоступным. Для вычисления подписи для текста 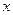, представленного числом, меньшим 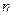и взаимно простым с 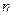, подписывающий возводит его в степень 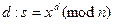. Подписанный текст представляет собой пару 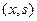. Для проверки подписи проверяющий вычисляет обратное преобразование и проверяет равенство 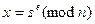. Если равенство выполняется, то подпись верна.

Алгоритм установления сеансового ключа

Поскольку операция возведения в степень коммутативна, т. е. , то можно использовать алгоритм Деффи-Хеллмана для установления сеансового ключа в кольце вычетов по модулю составного ключа. Для этого пользователи договариваются об общем числе 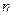и образующей 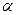циклической группы большого простого порядка. Пользователь А вырабатывает случайное число 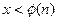, вычисляет и посылает пользователю В. Пользователь В вырабатывает свое случайное число - 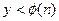, вычисляет 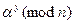и посылает пользователю А. Затем каждый из пользователей возводит полученное сообщение в степень со своим показателем и получает число 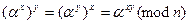, являющееся сеансовым ключом.