 |
|
Степенные ряды: радиус, интервал, область сходимости. Свойства степенных рядов. Теорема Абеля (с док-вом).
Для доказательства теоремы Абеля придется работать с функциональными рядами, поэтому, для начала нужно понять, что это такое и усвоить некоторые определения. (по желанию, возможно, будет легче понять…ежу)
Определение1. Ряд, члены которого являются функциями одной или
нескольких независимых переменных, определёнными на некотором множестве, называется функциональным рядом.
Рассмотрим функциональный ряд 
, члены которого являются функциями одной независимой переменной х. Сумма первых n членов ряда 
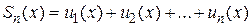является частичной суммой данного функционального ряда. Общий член 
есть функция от х, определённая в некоторой области.
Рассмотрим функциональный ряд в точке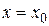 
. Если соответствующий числовой ряд 
сходится, т.е. существует предел частичных сумм этого ряда 
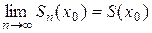(где 
− сумма числового ряда), то точка 
называется точкой сходимости функционального ряда 
. Если числовой ряд 
расходится, то точка называется точкой расходимости функционального ряда.
Определение2. («Это же элементарно, Ватсон») Областью сходимости функционального ряда называется множество всех таких значений х, при которых функциональный ряд сходится. Область сходимости, состоящая из всех точек сходимости, обозначается 
. Отметим, что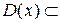 
R.
Функциональный ряд сходится в области , если для любого 
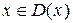он сходится как числовой ряд, при этом его сумма будет некоторой функцией 
. Это так называемая предельная функция последовательности 
: 
.
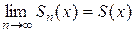Для нахождения области сходимости функционального ряда можно использовать признак, аналогичный признаку Даламбера. («А что это за признак?») Для ряда составляем 
и рассматриваем предел при фиксированном х: 
. Тогда является решением неравенства 
и решением уравнения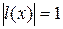 
(берём только те решения уравнения, в
которых соответствующие числовые ряды сходятся).
Практика в этой теме очень важна! Займемся ей!
Пример1. Найти область сходимости ряда 
.
Решение. (все, как на семинаре) Обозначим 
, 
. Составим и вычислим предел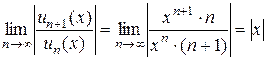 
, тогда область сходимости ряда определяется неравенством 
и уравнением 
. Исследуем дополнительно сходимость исходного ряда в точках, являющимися корнями уравнения:
а) если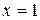 
, 
, то получается расходящийся ряд 
;
б) если 
, 
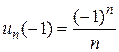, то ряд 
сходится условно по
признаку Лейбница. (надеюсь, что признак Лейбница запомнился)
Таким образом, область сходимости ряда 
имеет вид: 
.
Теперь займемся степенными рядами (кстати, это частный случай функционального ряда).
, где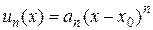 
.
Определение3. (Ой! Капитан, прекратите!) Степенным рядом называется функциональный ряд вида 
,
где 
− постоянные числа, называемые коэффициентами ряда.
Степенной ряд есть «бесконечный многочлен», расположенный по возрастающим степеням 
. Любой числовой ряд 
является
частным случаем степенного ряда при 
.
Рассмотрим частный случай степенного ряда при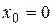 
: 
. Выясним, какой вид имеет
область сходимости данного ряда .