 |
|
Теорема: ТЕОРЕМА АБЕЛЯ.
1) Если степенной ряд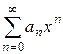 
сходится в точке 
, то он абсолютно сходится при всяком х, для которого справедливо неравенство 
.
2) Если же степенной ряд расходится при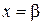 
, то он расходится при всяком х, для которого 
.
Доказательство.
1) По условию степенной ряд сходится в точке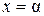 
, т. е. сходится числовой ряд
(1)
и по необходимому признаку сходимости («А что это за признак, помните?») его общий член стремится к 0, т.е.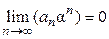 
. Следовательно, существует такое число 
, что все члены ряда ограничены этим числом: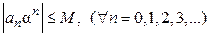 
.
Рассмотрим теперь любое х, для которого 
, и составим ряд из абсолютных величин: (А зачем? Читайте дальше.) 
.
Запишем этот ряд в другом виде: так как 
, то 
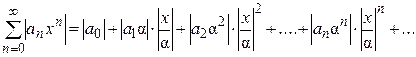(2).
Из неравенства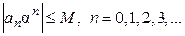 
получаем 
, т.е. ряд
(3)
состоит из членов, которые больше соответствующих членов ряда (2). Ряд 
представляет собой сходящийся ряд геометрической прогрессии со знаменателем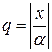 
, причём 
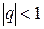, так как . СЛЕДОВАТЕЛЬНО (устроюсь работать следователем), ряд (2) сходится при . Таким образом, степенной ряд 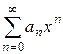абсолютно сходится.
2) Пусть ряд 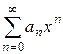расходится при 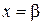, иными словами, расходится числовой ряд 
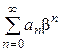. Докажем, что для любого х ( ) ряд расходится. Доказательство ведётся от противного. Пусть при некотором фиксированном 
( 
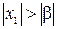) ряд сходится, тогда он сходится при всех 
(это следует из первой части данной теоремы), в частности, при 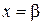, что противоречит условию 2) теоремы 1.
Теорема доказана.(Да-да. Вот так быстро. Советую перечитать пару раз этот пункт)
Следствие.
Теорема Абеля позволяет судить о расположении точки сходимости степенного ряда. Если точка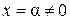 
является точкой сходимости степенного ряда, то интервал 
заполнен точками сходимости; если точкой расходимости является точка 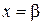, то
бесконечные интервалы 
заполнены точками расходимости (рис. 1).
Рис. 1. Интервалы сходимости и расходимости ряда
Можно показать, что существует такое число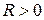 
, что при всех 
степенной ряд 
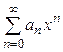абсолютно сходится, а при 
− расходится. Будем считать, что если ряд сходится только в одной точке 0, то 
, а если ряд сходится при всех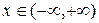 
, то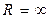 
.
Определение4. Интервалом сходимости степенного ряда 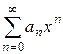называется такой интервал 
, что при всех 
этот ряд сходится и притом абсолютно, а для всех х, лежащих вне этого интервала, ряд расходится. Число R называется радиусом сходимости степенного ряда.
Замечание. На концах интервала вопрос о сходимости или расходимости степенного ряда решается отдельно для каждого конкретного ряда.
А теперь научимся определять интервал и радиус сходимости степенного ряда.
Рассмотрим степенной ряд 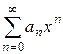и обозначим 
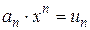. Составим ряд из абсолютных величин его членов:
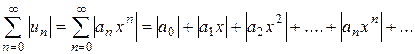
и применим к нему признак Даламбера. Пусть существует 
, где 
. По признаку Даламбера ряд сходится, если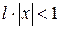 
, и расходится, если 
. Отсюда ряд сходится при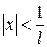 
, тогда интервал сходимости: 
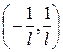. При 
ряд расходится, так как 
. Используя обозначение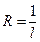 
, получим формулу для определения радиуса сходимости степенного ряда:
,
где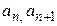 
− коэффициенты степенного ряда.
Если окажется, что предел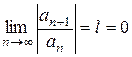 
, то полагаем 
.
Для определения интервала и радиуса сходимости степенного ряда также можно использовать радикальный признак Коши, радиус сходимости ряда определяется из соотношения 
.
Определение 5. Обобщенным степенным рядом называется ряд вида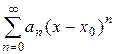 
. Его также называют рядом по степеням 
.
Для такого ряда интервал сходимости имеет вид: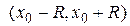 
, где 
− радиус сходимости.
Покажем, как находится радиус сходимости для обобщенного степенного ряда.
,
т.е. 
, где 
.
Если 
, то , и область сходимости 
R; если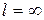 
, то и область сходимости 
.
Пример 2. Найти область сходимости ряда 
.
Решение. Обозначим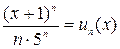 
. Составим предел
.
Решаем неравенство: 
, 
, следовательно, интервал
сходимости имеет вид: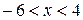 
, причём R = 5. Дополнительно исследуем концы интервала сходимости:
а) 
, 
, получаем ряд 
, который расходится;
б) 
, 
, получаем ряд 
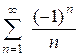, который сходится
условно. Таким образом, область сходимости: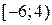 
, 
.
Ответ: область сходимости .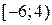
Пример 3. Ряд 
расходится для всех 
, так как 
при 
, радиус сходимости .
Пример 4. Ряд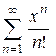 
сходится при всех 
R, радиус сходимости .