ЧАСТЬ 1. АРИФМЕТИКА ОСТАТКОВ. ЭЛЕМЕНТАРНЫЕ ШИФРЫ.

Стр 1 из 15Следующая ⇒

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

Брянский государственный технический университет

М.Ю. Рытов, И.Е. Грабежов

С.А. Шпичак

Математические основы криптологии.

Задачник-практикум.

Утверждено редакционно-издательским советом в качестве

учебного пособия

Брянск

Издательство БГТУ

УДК 621.391

Рытов М.Ю., Математические основы криптологии. Задачник-практикум/ М.Ю. Рытов, И.Е. Грабежов, С.А. Шпичак, – Брянск: БГТУ, 2014. – 60 с. – (Серия «Организация и технология защиты информации»)

ISBN

В пособии представлен сборник задач и рассматриваются теоретические вопросы построения асимметричных криптографических алгоритмов и протоколов.

Учебное пособие предназначено для студентов высших учебных заведений, обучающихся по направлению «Информационная безопасность» и специальности «Информационная безопасность автоматизированных систем», а также может быть полезно специалистам, интересующимся вопросами криптографического обеспечения защиты информации.

Ил.8. Табл.5. Библиограф. – 13 назв.

Рецензенты: Кафедра ”Электроника, вычислительная техника и информационная безопасность ” ФГОУВПО “Государственный университет - УНПК”; доктор технических наук профессор Лозбинев Ф.Ю.

ISBN 5-89838-357-3Ó Брянский государственный

технический университет, 2014

Ó М.Ю. Рытов, И.Е. Грабежов

С.А. Шпичак, 2010

ОГЛАВЛЕНИЕ

ВВЕДЕНИЕ. 4

ЧАСТЬ 1. АРИФМЕТИКА ОСТАТКОВ. ЭЛЕМЕНТАРНЫЕ ШИФРЫ. 6

Шифр Цезаря. 6

Аффинный шифр. 9

Обобщенный алгоритм Евклида. 10

Вскрытие аффинного шифра по двум паросочетаниям. 12

Варианты заданий к первой части. 13

ЧАСТЬ 2. БАЗОВЫЕ ТЕОРЕТИКО-ЧИСЛОВЫЕ АЛГОРИТМЫ. 14

Китайская теорема об остатках. 14

Возведение в квадрат. 15

Символы Лежандра и Якоби, извлечение квадратного корня. 16

Возведение в степень и нахождение порождающего элемента группы. 18

Генерация простых чисел. 20

Варианты заданий ко второй части. 21

ЧАСТЬ 3. АСИММЕТРИЧНЫЕ КРИПТОГРАФИЧЕСКИЕ ПРОТОКОЛЫ И СИСТЕМЫ ШИФРОВАНИЯ С ОТКРЫТЫМ КЛЮЧОМ. 22

Протокол Диффи-Хеллмана. 23

Трехпроходный протокол Шамира. 24

Криптосистема RSA. 26

Криптосистема Эль-Гамаля. 28

Криптосистема Рабина. 29

Варианты заданий к третьей части. 33

ЧАСТЬ 4. АСИММЕТРИЧНЫЕ СХЕМЫ ЭЛЕКТРОННО-ЦИФРОВОЙ ПОДПИСИ. 34

Цифровая подпись RSA. 34

Цифровая подпись Эль-Гамаля. 36

Генерация сильно простого числа и порождающего элемента. 38

Цифровая подпись DSA. 39

Варианты заданий к четвертой части. 41

ЧАСТЬ 5. ЭЛЛИПТИЧЕСКИЕ КРИВЫЕ НАД КОНЕЧНЫМ ПОЛЕМ. 42

Протокол Диффи-Хеллмана на эллиптических кривых. 46

Цифровая подпись EC-DSA. 47

Варианты заданий для пятой части. 49

ЗАКЛЮЧЕНИЕ ……………………………………………………………………………………. 50

Приложение 1. 51

Приложение 2. 52

Приложение 3. 56

СПИСОК ИСПОЛЬЗОВАННОЙ И РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ. 59

ВВЕДЕНИЕ

Пособие построено на принципе постепенного усложнения излагаемого материала. В случае недостаточного понимания текущего раздела, необходимо вернуться к повторению материалов предыдущих разделов.

Все примеры решения в пособии предваряются теоретическим введением с подробными комментариями. Непосредственно в решении приведены все промежуточные результаты, а комментарии наоборот - полностью отсутствуют. Оформление заданий при их выполнении оставляется на усмотрение преподавателя.

Ниже приведены примеры обозначений, используемых при описании алгоритмов и заданий [10]:

C_i, P, G - открытые параметры, которые могут быть известны противнику обозначаются заглавными символами;

k, x, q - секретные параметры, известные только корреспондентам (или только одному корреспонденту) обозначаются строчными символами;

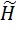– пример обозначения величины, подбираемой на данном этапе вычислений случайным или произвольным образом;

m, m’ – исходный и восстановленный, например, при расшифровании, параметры;

(mod N) - все операции выполняются по модулю (в остатках от деления) числа N.

Для лучшего понимания в последующем принципов программной реализации криптографических алгоритмов с большими числами все решения производить с последовательным приведением промежуточных значений по заданному модулю. В случае возникновения отрицательного промежуточного результата – тут же приводить его (прибавлять к нему модуль). Желательно, чтобы в решении не приводились отрицательные значения и значения, превышающие модуль по которому производятся вычисления.

Например, вместо:

(357 - 654) ∙ 46 (mod 701) = - 13662 mod 701 = 358

Производим последовательные вычисления:

(357 - 654) ∙ 46 (mod 701) = 404 ∙ 46 (mod 701) = 358

При решении задач рекомендуется использование встроенного калькулятора Windows, а также для реализации некоторых операций - редактора электронных таблиц MS Excel или Open Office Calc. Примеры реализации операций, таких как: вычисление мультипликативного обратного, модульное экспоненцирование, приведены в соответствующих разделах пособия. Все задания строятся на использовании относительно небольших чисел. В случае значительного увеличения значений исходных данных рекомендуется написание программ, реализующих отдельные действия на одном из языков программирования. Примеры исходных кодов таких программ на языках C# и Pascal приведены в приложении 2.

ЧАСТЬ 1. АРИФМЕТИКА ОСТАТКОВ. ЭЛЕМЕНТАРНЫЕ ШИФРЫ.

Шифр Цезаря.

Один из наиболее ранних и примитивных шифров простой замены. Изначально шифрование производилось при помощи записи двух алфавитов – открытого текста и шифртекста один под другим со смещением влево на величину сдвига k - ключа (см. рис.1). Считается, что Юлий Цезарь, которому приписывается авторство этого шифра, использовал ключ k = 3. При зашифровании символы заменяются сверху вниз, а при расшифровании, соответственно – снизу вверх.

A	B	C	D	E	. . .	W	X	Y	Z
D	E	F	G	H	. . .	Z	A	B	C

Рис.1. Шифр Цезаря

Для построения функций зашифрования и расшифрования этого шифра более удобным будет представление шифратора в виде двух соосных колец (см. рис.2), на каждом из которых нанесены N символов алфавита. Ключом является угол поворота k внутреннего кольца относительно внешнего, выраженный в количестве символов.

Рис.2. Дисковый шифратор

Для удобства перехода к математической модели вместо символов будем использовать их порядковые номера от 0 до N - 1. И зашифрование и расшифрование будем производить сверху-вниз. Для этого при зашифровании внутреннее кольцо будем поворачивать на k делений против часовой стрелки, а при расшифровании на k делений по часовой стрелке, или на N – k делений против часовой стрелки, что одно и то же.

Таким образом, количество возможных ключей шифра Цезаря – (N – 1), за исключением сдвига на величину 0 º N. Математически выразим функции зашифрования и расшифрования для шифра Цезаря. Операцией наложения ключа является сложение по модулю N.

Функция зашифрования : ,

Функция расшифрования: ,

где:

m_i – i-ый символ открытого текста,

C_i – i-ый символ шифртекста, k – ключ зашифрования,

- ключ расшифрования.

Задача 1.1. Осуществить зашифрование и расшифрование символа m₁ на алфавите N при помощи шифра Цезаря на ключе k. Проверить правильность расшифрования.

Пример решения.

Дано: k = 7 m₁ = 24 N = 26	Решение:
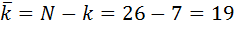
Найти: C₁, 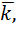m₁’ Проверить: m₁’ = m₁

Недостаток операции сложения заключается в ее линейности (см. столбец 2 табл. 1), что позволяет восстановить ключ k уже по одному известному паросочетанию m_i « C_i для чего достаточно решить одно линейное сравнение:

Несколько лучшие характеристики перемешивания дает операция модульного умножения (см. столбец 3 табл. 1), но здесь первым недостатком является то, что элемент 0 всегда будет зашифрован как 0. Вторым недостатком считается то, что в качестве ключа по умножению можно использовать не все значения алфавита N, а только взаимно простые с N. Например, при попытке использовать k = 2 (см. столбец 5 табл. 1) не удается добиться однозначности расшифрования – одному шифробозначению соответствует две шифрвеличины. Например 6 может быть расшифровано как 3 или 7.

Таблица 1

N=8, k₂=2
m	k = k₁ = 3	k = 2
m+k(mod N)	m×k(mod N)	m×k₁+k₂(mod N)	m×k(mod N)

Первый недостаток исправляется введением дополнительной операции сложения, а второй – ограничением пространства ключей:

Нахождение наибольшего общего делителя возможно при помощи основной теоремы арифметики [11]:

Например для 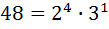: 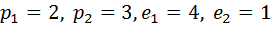, то есть k₁ не должен делиться на 2 и 3, но ввиду высокой вычислительной сложности метода на практике применяют алгоритм Евклида.

Количество элементов алфавита, пригодных для шифрования при помощи умножения определяется функцией Эйлера:

Например: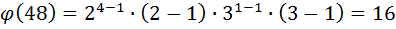

Особый интерес представляют частные случаи функции Эйлера от простого числа и от произведения двух простых чисел (при известных p и q):

На основании вышеизложенного приведем модель аффинного шифра.

Аффинный шифр.

Шифрование осуществляется посимвольно на алфавите N. Используется два ключа k₁ и k₂ и две операции их наложения – соответственно умножение и сложение по модулю N.

Функция зашифрования:

Функция расшифрования:

где:

m_i – i-ый символ открытого текста,

C_i – i-ый символ шифртекста,

k₁ – ключ зашифрования по умножению,

k₂ – ключ зашифрования по сложению,

- ключ расшифрования по умножению,

- ключ расшифрования по сложению.

Отдельно следует рассмотреть вопрос нахождения мультипликативного обратного. На практике для этого применяют обобщенный (расширенный) алгоритм Евклида.

12 3 4 5 6 7 8 9 10 Следующая ⇒