Главная | Обратная связь

ЧАСТЬ 3. АСИММЕТРИЧНЫЕ КРИПТОГРАФИЧЕСКИЕ ПРОТОКОЛЫ И СИСТЕМЫ ШИФРОВАНИЯ С ОТКРЫТЫМ КЛЮЧОМ.

Базой асимметричных криптографических протоколов и алгоритмов является использование однонаправленных функций и однонаправленных функций с лазейкой (секретом) [12].

Основные кандидаты на однонаправленные функции:

1) Перемножение двух больших простых чисел. Обратное преобразование называют факторизацией – разложением на множители.

2) Модульное возведение в степень (экспоненцирование) в конечном поле при фиксированном основании. Обратное преобразование называют дискретным логарифмированием.

Основным кандидатом на однонаправленную функцию с лазейкой (секретом) является модульное экспоненцирование c фиксированным показателем в конечном кольце Z_N, где N является произведением двух больших простых чисел.

Рассмотрим вопросы извлечения корня произвольной степени по модулю простого и составного чисел.

В основе операции извлечения корня в конечном поле лежит Малая теорема Ферма:

Для начала приведем доказательство следующего утверждения [9]:

Любое натуральное y может быть представлено в виде: 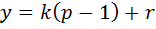, отсюда

{применяя малую теорему Ферма}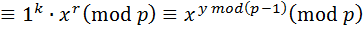

Из вышеуказанного следует, что извлечение корня степени y по модулю p возможно лишь для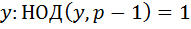

Таким образом:

В основе операции извлечения корня в конечном поле лежит обобщение Эйлера для малой теоремы Ферма:

Опустив промежуточные выкладки по аналогии с предыдущим случаем получаем, что извлечение корня степени y по модулю составного числа N возможно лишь для

и реализуется как:

,

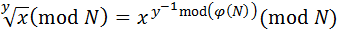при этом обязательно необходимо знать разложение N = p ∙ q – секрет, без которого невозможно эффективное вычисление значения функции Эйлера φ(N).

Далее рассмотрим несколько базовых асимметричных протоколов и алгоритмов шифрования.