 |
|
Задача 1. Элементы теории графов
КОНТРОЛЬНАЯ РАБОТА
ВАРИАНТ № 8
Задача 1. Элементы теории графов
Связный ориентированный граф G(Х, Г) задан множеством вершин X={x1, x2,…, xn} и отображением Гxi={x|I±k|, x|I±l|}, i =1, 2,…, n. Здесь i – текущий номер вершины, n- количество вершин графа. Значение индексов n, k и l взять из табл. 1 в соответствии с номером варианта. Индексы k и l формируют значения индексов a, b , g… переменной x в отображении Гxi = {xa , xb , xg,…}. Если значения индексов a, b, g… переменной x не соответствуют ни одному из номеров вершин графа, то эта переменная не учитывается во множестве Гxi.
Выполнить следующие действия:
а) определить исходный граф и ассоциированный с ним неориентированный граф графическим, матричным и аналитическим способами;
б) установить центры и периферийные вершины графов, найти радиусы и диаметры графов;
в) выделить в ориентированном графе два подграфа. Найти объединение, пересечение и разность подграфов;
г) описать систему уравнений, соответствующую сигнальному графу, считая, что передача между вершинами xi и xj
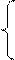i*j при i ³ j;
Kij =
1/(p+1) при i<j .
Найти передачу между вершинами x1 и xn, используя правило Мезона. Построить структуру кибернетической системы, определяемой топологией графа.
Таблица 1
| № варианта | |||||||||||||||
| N | |||||||||||||||
| K | |||||||||||||||
| L | |||||||||||||||
| № варианта | |||||||||||||||
| N | |||||||||||||||
| K | |||||||||||||||
| L |
Решение:
Множество вершин X = {x1, x2, x3, x4, x5}, n = 5, k = 5, l = 1. Гxi={x|I±k|, x|I±l|}.
а) определим исходный граф и ассоциированный с ним неориентированный граф графическим, матричным и аналитическим способами:
Определим граф аналитическим способом:
Гx1 = { x4, x2 };
Гx2 = { x3, x1 };
Гx3 = { x2, x4 };
Гx4 = { x1, x5, x3};
Гx5 = {x4}.
Ориентированный граф графическим способом:
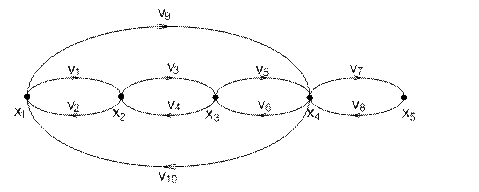
Неориентированный граф графическим способом:
Ориентированный граф матричным способом:
RG – матрица смежности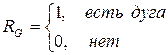 
| x1 | x2 | x3 | x4 | x5 | |
| x1 | |||||
| x2 | |||||
| x3 | |||||
| x4 | |||||
| x5 |
AG – матрица инцидентности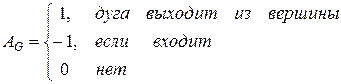 
| v1 | v2 | v3 | v4 | v5 | v6 | v7 | v8 | v9 | v10 | |
| x1 | -1 | -1 | ||||||||
| x2 | -1 | -1 | ||||||||
| x3 | -1 | -1 | ||||||||
| x4 | -1 | -1 | -1 | |||||||
| x5 | -1 |
Неориентированный граф матричным способом:
RD – матрица смежности
| x1 | x2 | x3 | x4 | x5 | |
| x1 | |||||
| x2 | |||||
| x3 | |||||
| x4 | |||||
| x5 |
AD – матрица инцидентности
| v1 | v2 | v3 | v4 | v5 | v6 | v7 | v8 | v9 | v10 | |
| x1 | ||||||||||
| x2 | ||||||||||
| x3 | ||||||||||
| x4 | ||||||||||
| x5 |
б) установить центры и периферийные вершины графов, найти радиусы и диаметры графов:
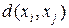– матрица отклонений; 
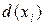– вектор отклонения.
| x1 | x2 | x3 | x4 | x5 | |
| x1 | |||||
| x2 | |||||
| x3 | |||||
| x4 | |||||
| x5 |
=>
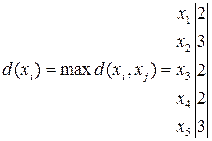Центры графа – это вершины с наименьшей удаленностью. Периферийные вершины - вершины с наибольшей удаленностью. В данном случае периферийными вершинами являются две вершины x2, x4,а центрами графа являются три вершины x1, x3, x5. Тогда радиус ρ(G) =2, а диаметр графа D(G) = 3.
в) выделим в ориентированном графе два подграфа и найдем объединение, пересечение и разность подграфов:
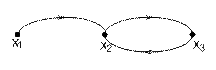
Выделяем два подграфа: G1 и G2
X1 – {x1, x2}, Г1х1 = { x2 }, Г1х2 = {x1},
X2 – {x1, x2, x3}, Г2х1 = {x2}, Г2х2 = {x3}, Г2х3 = {x2}.
Объединение графов: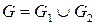 
,
, 
, 
, 
.
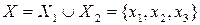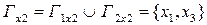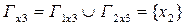G
Пересечение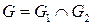 
,
, 
, 
.
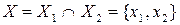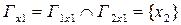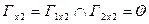G
Разностью графов G1(X1, Г1) и G2(X2, Г2) называется граф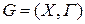 
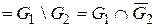, где 
– дополнение по отображению графа G2 до насыщенного.
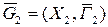, где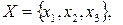 
.
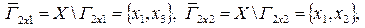
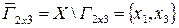Он имеет вид
; 
, 
.
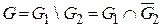Граф имеет вид:
G 
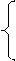г) i*j при i ³ j;
Kij = 1/(p+1) при i<j .
Сигнальный граф имеет вид
Система уравнений, соответствующая сигнальному графу имеет вид
x1 = 2 x2 + 4x4
x2 =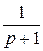 
x1 +6x3
x3 = 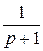x2 +12 x4
x4 = 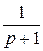x1 + 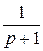x3 +20x5
x5 = 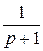x4.
Определить передачу k15 по правилу Мезона. Формула Мезона имеет вид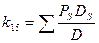 
PS – передача пути,
DS – алгебраическое дополнение,
D – определитель.
Пути из х1 в х5:
.
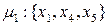
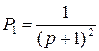
Контура:
; 
; 
;
; 
.
;
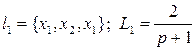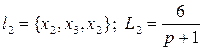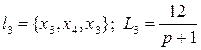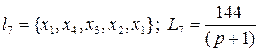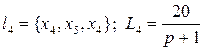Пары несоприкасающихся контуров L1L3, L1L4, L2L4, L2L5.
Отсюда
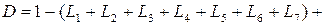(L1L3+ L1L4+ L2L4+ L2L5).
D1 = 1- L2
D2 = 1.
.
Структура кинематической системы представлена на рисунке
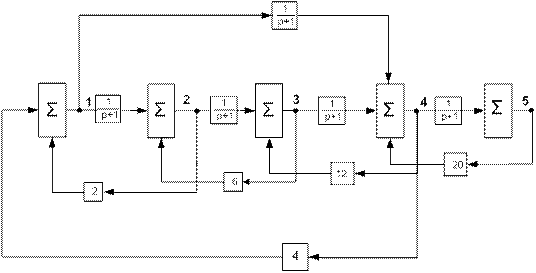
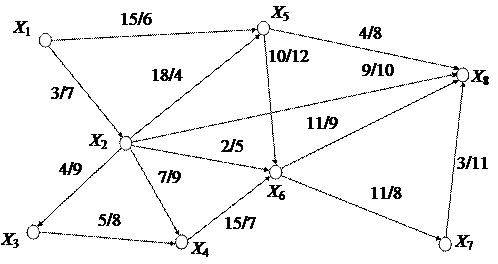
Задача 2. Задача о максимальном потоке
и потоке минимальной стоимости
На рисунке приведена транспортная сеть в виде ориентированного графа. На каждом из ребер через черту проставлены значения пропускной способности С(n) ребра n и стоимость транспортировки единицы потока d(n) по этому ребру. Для заданной сети определить:
1) максимальный поток jmax транспортировки груза между указанной парой вершин, считая одну из них источником, а другую — стоком.
2) стоимость доставки груза по путям, формирующим максимальный поток в сети.
 |
Решение:
1) найдем максимальный поток jmax транспортировки груза между вершинами х1 и х8.
Первый шаг. 1. Находим какой-либо путь из х1 в х8 с положительной пропускной способностью.
Таблица 1
| x1 | x2(1) | x3(2) | x4(2) | x5(1) | x6(2) | x7(6) | x8(2) | |
| x1 | 3- | |||||||
| x2 | 0+ | 9- | ||||||
| x3 | ||||||||
| x4 | ||||||||
| x5 | ||||||||
| x6 | ||||||||
| x7 | ||||||||
| x8 | 0+ |
В результате получен путь l1 = (x1,x2,x8). Элементы этого пути Cij помечаем знаком минус, а симметричные элементы Cji – знаком плюс.
Определяем пропускную способность найденного пути, которая равна наименьшей из пропускных способностей дуг:
Определяем остаточные пропускные способности дуг найденного пути и симметричных ему дуг. Для этого из элементов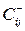 
табл. 1 вычитаем C1, а к элементам 
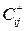прибавляем C1. В результате получим новую табл. 2 с измененными пропускными способностями.
Tаблица 2
| x1 | x2 | x3 | x4 | x5(1) | x6(5) | x7(6) | x8(5) | |
| x1 | 15- | |||||||
| x2 | ||||||||
| x3 | ||||||||
| x4 | ||||||||
| x5 | 0+ | 4- | ||||||
| x6 | ||||||||
| x7 | ||||||||
| x8 | 0+ |
Второй шаг. 1. Помечаем столбцы табл. 2, находим второй путь l2 = (x1, x5, x8) и расставляем знаки.
2. Пропускная способность пути l2
Изменим пропускные способности помеченных дуг на С2 в табл. 3.
Tаблица 3
| x1 | x2 | x3 | x4 | x5(1) | x6(5) | x7(6) | x8(6) | |
| x1 | 11- | |||||||
| x2 | ||||||||
| x3 | ||||||||
| x4 | ||||||||
| x5 | 4+ | 10- | ||||||
| x6 | 0+ | 11- | ||||||
| x7 | ||||||||
| x8 | 0+ |
Третий шаг. 1. Помечаем столбцы табл. 3, находим третий путь l3 = (x1, x5, x6, x8) и расставляем знаки.
2. Пропускная способность пути l2
Изменим пропускные способности помеченных дуг на С3 в табл. 4.
Tаблица 4
| x1 | x2 | x3 | x4 | x5(1) | x6 | x7 | x8 | |
| x1 | ||||||||
| x2 | ||||||||
| x3 | ||||||||
| x4 | ||||||||
| x5 | ||||||||
| x6 | ||||||||
| x7 | ||||||||
| x8 |
Четвертый шаг. Просматривая строки, убеждаемся в том, что больше не существует ни одного пути с положительной пропускной способностью из вершины x1 в вершину x8. Подмножество R образуют помеченные вершины х1, х5, а подмножество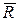 
– остальные непомеченные вершины х2, х3, х4, х6, х7, х8. Разрез с минимальной пропускной способностью образуют дуги, начальные вершины которых принадлежат подмножеству R, а конечные – 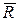. Таким образом, разрез с минимальной пропускной способностью 
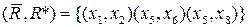. Удалив дуги этого разреза, блокируем все пути из источника в сток. Пропускная способность разреза
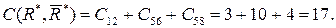
Заключительный шаг. Вычитая из элементов табл.1 соответствующие элементы табл.4, получим табл.5
Tаблица 5
| x1 | x2 | x3 | x4 | x5 | x6 | x7 | x8 | |
| x1 | ||||||||
| x2 | -3 | |||||||
| x3 | ||||||||
| x4 | ||||||||
| x5 | -14 | |||||||
| x6 | -10 | |||||||
| x7 | ||||||||
| x8 | -3 | -4 | -10 |
Величина максимального потока равна сумме элементов x1-й строки табл. 5 или сумме элементов x8-го столбца
Максимальный поток равен 
.
2) положительные элементы табл.5 характеризуют величины дуговых потоков:
; 
; 
; 
; 
; 
.
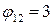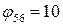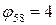Стоимость доставки груза определяется по формуле:
.
.
.
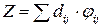
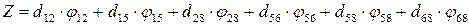