Главная | Обратная связь

Угорський метод розв’язання транспортної задачі про призначення

Угорський метод є одним з найцікавіших і найпоширеніших методів рішення транспортних завдань. Основна ідея цього методу була вперше висловлена угорським математиком Е. Егерварі (звідси й назва методу) задовго до виникнення теорії лінійного програмування.

Розглянемо спочатку основні ідеї угорського методу на прикладі рішення завдання вибору (завдання про призначення), що є окремим випадком транспортної задачі, а потім узагальнимо цей метод для довільної транспортної задачі.

Припустимо, що є різні транспортні засоби (ТЗ), кожний з яких може виконувати будь-яку транспортну роботу, але з неоднаковою ефективністю. Продуктивність кожного i-го ТЗ при виконанні j-тої транспортної роботи позначимо C_ij , і = 1, … ,n; j = 1, … ,n. Потрібно так розподілити ТЗ по роботах, щоб сумарний ефект від їхнього використання був максимальний. Таке завдання називається завданням вибору або завданням про призначення.

Формально вона записується так. Необхідно вибрати таку послідовність елементів з матриці

щоб сума була максимальна й при цьому з кожного рядка й стовпця був обраний тільки один елемент.

Незалежний нуль: нульовий елемент матриці називається незалежним нулем, якщо рядок і стовпчик, на пересіченні яких він знаходиться, не містить інших нулів.

Еквівалентні матриці С і D (C ~ D), якщо с_ij = d_ij + a_i + b_j для всіх i,j.

Виділені елементи – елементи, які розташовані у виділених рядках або стовпчиках. Блок-схема алгоритму угорського методу наведена нижче:

Попередній етап. Розшукують максимальний елемент в j-му стовпці й всі елементи цього стовпця послідовно віднімають із максимального. Цю операцію проробляють над всіма стовпцями матриці С. У результаті утвориться матриця з ненегативними елементами, у кожному стовпці якої є, принаймні, один нуль.

Далі розглядають i-ий рядок отриманої матриці, розшукують її мінімальний елемент і з кожного елемента цього рядка віднімають мінімальний. Цю процедуру повторюють із усіма рядками. У результаті одержимо матрицю С₀ (С₀ ~ C), у кожному рядку й стовпці якої є, принаймні, один нуль. Описаний процес перетворення С у С₀ називається приведенням матриці.

Знаходимо довільний нуль у першому стовпці й відзначаємо його зірочкою. Потім переглядаємо другий стовпець, і якщо в ньому є нуль, розташований у рядку, де немає нуля із зірочкою, то відзначаємо його зірочкою. Аналогічно переглядаємо один за іншим всі стовпці матриці С₀ і відзначаємо, якщо можливо, що випливають нулі знаком '*'. Очевидно, що нулі матриці С₀, відзначені зірочкою, є незалежними. На цьому попередній етап закінчується.

(k+1)-а ітерація. Припустимо, що k-та ітерація вже проведена й у результаті отримана матриця С_k. Якщо в ній є рівно n нулів із зірочкою, то процес рішення закінчується. У противному випадку переходимо до (k+1) –ої ітерації.

Кожна ітерація починається першим і закінчується другим етапом. Між ними може кілька разів проводитися пари етапів: третій - перший. Перед початком ітерації знаком '+' виділяють стовпці матриці С_k, які містять нулі із зірочками.

Перший етап. Переглядають невиділені стовпці С_k. Якщо серед них не виявиться нульових елементів, то переходять до третього етапу. Якщо ж невиділений нуль матриці С_k виявлений, то можливо один із двох випадків:

1) рядок, що містить невиділений нуль, містить також і нуль із зірочкою;

2) цей рядок не містить нуля із зірочкою.

У другому випадку переходимо відразу до другого етапу, відзначивши цей нуль штрихом.

У першому випадку цей невиділений нуль відзначають штрихом і виділяють рядок, у якій він утримується (знаком '+' праворуч від рядка). Переглядають цей рядок, знаходять нуль із зірочкою й знищують знак '+' виділення стовпця, у якому втримується даний нуль.

Далі переглядають цей стовпець (який уже став невиділеним) і відшукують у ньому невиділений нуль (або нулі), у якому він перебуває. Цей нуль відзначають штрихом і виділяють рядок, що містить такий нуль (або нулі). Потім переглядають цей рядок, відшукуючи в ній нуль із зірочкою.

Цей процес за кінцеве число кроків закінчується одним з наступних результатів:

1) всі нулі матриці С_k виділені, тобто перебувають у виділених рядках або стовпцях. При цьому переходять до третього етапу;

2) є такий невиділений нуль у рядку, де немає нуля із зірочкою. Тоді переходять до другого етапу, відзначивши цей нуль штрихом.

Другий етап. На цьому етапі будують наступний ланцюжок з нулів матриці С_k: вихідний нуль зі штрихом, нуль із зірочкою, розташований в одному стовпці з першим нулем зі штрихом в одному рядку з попереднім нулем із зірочкою й т.д. Отже, ланцюжок утвориться пересуванням від 0^' до 0^* по стовпці, від 0^* до 0^' по рядку й т.д.

Можна довести, що описаний алгоритм побудови ланцюжка однозначний і кінцевий, при цьому ланцюжок завжди починається й закінчується нулем зі штрихом.

Далі над елементами ланцюжка, що знаходяться на непарних місцях ( 0^' ) ставимо зірочки, знищуючи їх над парними елементами (0^*). Потім знищуємо всі штрихи над елементами С_k і знаки виділення '+'. Кількість незалежних нулів буде збільшено на одиницю. На цьому (k+1)-а ітерація закінчена.

Третій етап. До цього етапу переходять після першого, якщо всі нулі матриці С_k виділені. У такому випадку серед невиділених елементів С_k вибирають мінімальний і позначають його h (h>0). Далі віднімають h із всіх елементів матриці С_k, розташованих у невиділених рядках і додають до всіх елементів, розташованим у виділених стовпцях. У результаті одержують нову матрицю С_k^', еквівалентну С_k. Помітимо, що при такому перетворенні, всі нулі із зірочкою матриці С_k залишаються нулями й у С_k^', крім того, у ній з'являються нові невиділені нулі. Тому переходять знову до першого етапу. Завершивши перший етап, залежно від його результату або переходять до другого етапу, або знову повертаються до третього етапу.

Після кінцевого числа повторень черговий перший етап обов'язково закінчиться переходом на другий етап. Після його виконання кількість незалежних нулів збільшиться на одиницю й (k+1)-а ітерація буде закінчена.

Нехай в результаті вирішення основної транспортної задачі ми отримали оптимальні обсяги перевезень x_ij>=0 у кількості (m+n–1). З урахуванням матриці відстаней можна отримати відповідну матрицю обсягів транспортної роботи (ТР) , причому кількість її ненульових елементів також дорівнює (m+n–1).

Перенумеруємо всі ненегативні обсяги A_TPij від 1 до (m+n–1), рухаючись послідовно по кожному рядку матриці обсягів ТР зверху до низу. В результаті отримуємо матрицю-строку А = {A_j}, ( 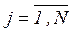), де N = (m+n– 1) – кількість необхідних ТР.

Припустимо, що для виконання спланованих обсягів перевезень передбачено також N транспортних засобів (ТЗ), кожний з котрих характеризується деякою продуктивністю виконання одиниці тієї чи іншої ТР (П_ij – продуктивність виконання i – м ТЗ j – ї ТР, де , ). Очевидно, що термін виконання j – ї ТР i – им ТЗ дорівнює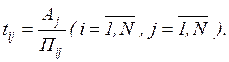

З метою застосування при розв’язанні цієї задачі алгоритму угорського методу призведемо з матрицею T_рч – матрицею робочого часу виконання ТЗ відповідних транспортних робіт наступні перетворення, а саме:

- знайдемо у матриці T максимальне значення – саму довгу за терміном виконання транспортну роботу;

- потім порахуємо за який робочий час t_роб буде вона виконана, причому час виконання буде кратним 8 (кількості робочих годин у зміну);

- побудуємо нову матрицю T_вч, елементи якої означають вільний час, який залишиться після виконання усіма ТЗ відповідних транспортних робіт.

При такому розгляді проблеми стає актуальною задача розподілу N транспортних засобів, що забезпечує максимальний загальний строк вільного часу, який залишився після виконання всього комплексу зазначених транспортних перевезень, тобто

, (1)

при обмеженні, що один ТЗ може бути призначений лише для виконання однієї ТР з зазначеного комплексу робіт.