 |
|
Числове розв’язання диференціального рівняння
Лабораторна робота № 1
(явна схема)
Більшість різноманітних процесів (фізичних, теплових, газодинамічних тощо) описуються диференціальними рівняннями першого чи другого порядку. У загальному випадку ці рівняння не мають аналітичного рішення, яке подається елементарними функціями (наприклад розподіл температури в тілі). Такі рівняння розв’язують числовим методом, який є методом наближеним, але при певних умовах дає задовільний збіг з точним рішенням.
Метою лабораторної роботи є числовий розрахунок за явною схемою поля температур в металевій штабі в залежності від часу, який описується диференціальним рівнянням другого порядку в часткових похідних. Задача, яка пропонується до розв’язання, є нестаціонарною, оскільки поле температур передбачається визначати в залежності від часу.
Для визначення поля температур необхідно скласти програму розрахунків і візуалізації отриманих результатів на екрані монітора комп’ютера будь-якою алгоритмічною мовою. З метою полегшення реалізації поставленої задачі на ПЕОМ нижче наведено текст програми у псевдокоді.
Отже, визначимо розподіл температури 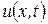 в металевій штабі для будь-якого значення часу
в металевій штабі для будь-якого значення часу  за умови, що фізичні властивості матеріалу штаби є величинами сталими.
за умови, що фізичні властивості матеріалу штаби є величинами сталими.
У виразі 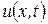 під
під  розуміється температура, під х – поздовжня координата, а під
розуміється температура, під х – поздовжня координата, а під  – час.
– час.
Розподіл температури в металевій штабі може бути описаним наступним диференціальним рівнянням з початковими та граничними умовами:
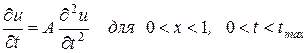 (1)
(1)
 (2)
(2)
де А – стала величина, яка залежить від теплопровідних здібностей матеріалу, з якого виготовлено штабу, а також від деяких інших чинників.
Поставлену задачу краще розв’язувати в безрозмірних одиницях. На рис. 1 показано металеву штабу одиничної довжини.

Для числового розв’язання поставленої задачі апроксимуємо диференціальне рівняння (1) разом з початковими і граничними умовами (2) кінцевими різницями.
Для цього побудуємо сітку в області, обмеженій  і
і  (рис. 2), з кроком
(рис. 2), з кроком 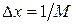 і
і  , де M і N – деякі цілі числа. Під функцією
, де M і N – деякі цілі числа. Під функцією  будемо розуміти апроксимацію рівняння (1) кінцевими різницями.
будемо розуміти апроксимацію рівняння (1) кінцевими різницями.

Для будь-якого вузла сітки (i, j), для якого лічильник і не дорівнює 0 та M, а лічильник j не дорівнює 0, похідні диференціального рівняння (1) можна замінити кінцевими різницями наступним чином:

Тоді рівняння (1) наближено замінюється виразом:

Звідки отримують
 (3)
(3)
Нас буде цікавити температура в точці 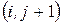 , тому розв'яжемо рівняння (3) відносно температури в точці
, тому розв'яжемо рівняння (3) відносно температури в точці 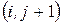
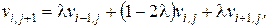 (4)
(4)
де
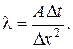
Таким чином, із диференціального рівняння (1) отримано зв'язок між температурою наступного шару (j + 1) і поточного шару (j).
 |
На рис. 3 хрестиками і маленькими колами позначені ті вузли сітки, які задіяні при визначенні похідних у рівнянні (4).
Якщо для будь-якого рівня часу  відомі значення температури
відомі значення температури  , то з рівняння (4) можна безпосередньо визначити значення температури при
, то з рівняння (4) можна безпосередньо визначити значення температури при  , тобто в шарі (j + 1). Подібна схема розрахунку має назву явною.
, тобто в шарі (j + 1). Подібна схема розрахунку має назву явною.
Але при цьому виникають певні питання. Так, де взяти значення температури в нульовому шарі, тобто при  ? Зазначимо, що для визначення значень температури в нульовому шарі застосовуються визначені вище початкові умови, які записуються у вигляді:
? Зазначимо, що для визначення значень температури в нульовому шарі застосовуються визначені вище початкові умови, які записуються у вигляді:
 (5)
(5)
Подібні ж питання постають для граничних точок, що мають значення лічильника і, які дорівнюють 0 і М. Виходячи з граничних умов, можна зробити висновки, що
 (6)
(6)
Застосувавши початкові умови у вигляді (5) і граничні умови у вигляді (6), можна за рівнянням (4) розрахувати значення температур у шарі (j = 1) і продовжити розрахунки до шару з номером N, тобто поступово збільшуючи час прогріву штаби.
Розглянемо процес зміни температури у штабі з паралельними сторонами  за умови, що відомий коефіцієнт α її теплопровідності та в початковий момент часу
за умови, що відомий коефіцієнт α її теплопровідності та в початковий момент часу  температура
температура  рівномірно розподілена вздовж штаби. Дві взаємно протилежні сторони знаходяться при постійній температурі
рівномірно розподілена вздовж штаби. Дві взаємно протилежні сторони знаходяться при постійній температурі  . Необхідно знайти розподіл температури залежно від часу та координати розташування пробної точки.
. Необхідно знайти розподіл температури залежно від часу та координати розташування пробної точки.
Рівняння теплопровідності має наступний вигляд:
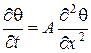 . (7)
. (7)
Уведемо для розгляду безрозмірні величини



Тоді рівняння (7) може бути переписаним і поданим у наступному вигляді:
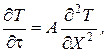
яке будемо розв’язувати за наявності таких умов:

За цих обставин початкові і граничні умови приймуть просту форму:


Слід зазначити, що модифікацією функціональних залежностей 
 для початкових і граничних умов можна розрахувати відповідне поле температур.
для початкових і граничних умов можна розрахувати відповідне поле температур.
 |