 |
|
Числове розв’язання диференціального рівняння
(неявна схема)
Метою лабораторної роботи є числовий розрахунок за неявною схемою поля температур в металевій штабі в залежності від часу та порівняння отриманих результатів з результатами розрахунків за явною схемою.
У вище розглянутому прикладі застосування явного методу розв’язання диференціального рівняння (1) апроксимовані температури  у вузлах сітки залежали тільки від
у вузлах сітки залежали тільки від 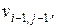
 i
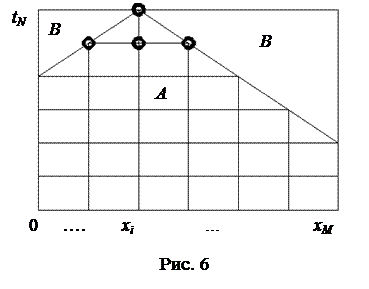
i  . З розгляду рис. 6 випливає, що за цим підходом визначення величин температури v можливе тільки в зоні, позначеній літерою А. Саме вузли цієї зони задіяні при визначенні розподілу температури в штабі. У той же час відомо, що для визначення поля температур, обумовленого диференціальним рівнянням (1) та початковими і граничними умовами (2), необхідно проводити розрахунки як зоні А, так і в зоні В.
. З розгляду рис. 6 випливає, що за цим підходом визначення величин температури v можливе тільки в зоні, позначеній літерою А. Саме вузли цієї зони задіяні при визначенні розподілу температури в штабі. У той же час відомо, що для визначення поля температур, обумовленого диференціальним рівнянням (1) та початковими і граничними умовами (2), необхідно проводити розрахунки як зоні А, так і в зоні В.
 |
Розв’яжемо рівняння (1) з початковими і граничними умовами (2), розглянутими в лабораторній роботі 1, за дещо іншою схемою апроксимаційного подання похідних, яку називають неявною схемою. Запишемо кінцеві різниці похідних у наступному вигляді:
 (8)
(8)
 |
На відміну від попереднього прикладу, коли друга похідна визначалася в j-му шарі з часом
 , зараз вона знаходиться зі значеннями апроксимованої температури в шарі j+1, якому відповідає час
, зараз вона знаходиться зі значеннями апроксимованої температури в шарі j+1, якому відповідає час  . Це призводить до іншої схеми розташування чотирьох вузлових точок, задіяних в обчислювальному процесі. Схема їх розташування показана на рис. 7.
. Це призводить до іншої схеми розташування чотирьох вузлових точок, задіяних в обчислювальному процесі. Схема їх розташування показана на рис. 7.
Розв’яжемо рівняння (8) відносно  , яке запишемо в правій частині розв’язку. Будемо мати вираз:
, яке запишемо в правій частині розв’язку. Будемо мати вираз:
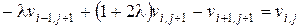 . (9)
. (9)
Коефіцієнт λ має той же сенс, що і в роботі № 1.
Граничні та початкові умови залишаються тими ж самими, що й лабораторній роботі № 1:
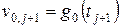 ,
,
 ,
,
 .
.
Рівняння (9) можуть бути записані для кожної вузлової точки з діапазону 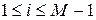 для будь-якого моменту часу, що призведе до системи з М – 1 рівнянь з М – 1 невідомими
для будь-якого моменту часу, що призведе до системи з М – 1 рівнянь з М – 1 невідомими  .
.
Розглянемо розв’язання наступної системи лінійних рівнянь:
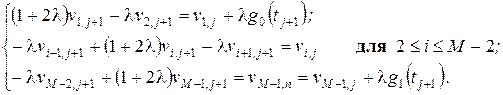 (10)
(10)
Цю систему рівнянь зручніше записати в такому вигляді:
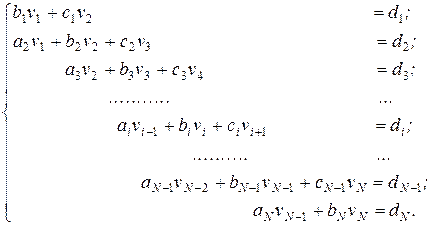 (11)
(11)
У системах (10) і (11) для скорочення запису індекси (j + 1) при всіх температурах v пропущені. Праві частини рівнянь (10), які є відомими величинами, для спрощення запису позначені як 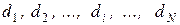 , де
, де 
Система рівнянь (11) має назву тридіагональної матриці, оскільки заповненими є тільки три діагональні елементи кожного рядка. Цю систему можна розв’язати відомим методом Гауса, але при цьому мають бути заповнені всі нульові члени, тому матриця буде мати значний розмір і буде виконано багато зайвих обчислювальних операцій, що є недоцільним.
Краще для розв’язання тридіагональної матриці застосовувати так званий рекурсивний метод у наступній формі:
 . (12)
. (12)
Коефіцієнти bi і γi будуть розглянуті трошки нижче.
Підстановка виразу (12) в систему (11) призведе до наступного запису:
 ,
,
з якого можна визначити vi:
 .
.
Це дає можливість застосувати наступну рекурсивну схему:
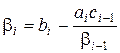 ;
;  ,
,
З першого рівняння системи (11) маємо
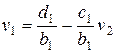 ,
,
де 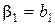 .
.
Коефіцієнт γ1 дорівнює 
Із останнього рівняння системи (11) можна отримати
 .
.
Звідки
 .
.
Таким чином, алгоритм розв’язання тридіагональної матриці у стислому вигляді запишеться наступним чином:
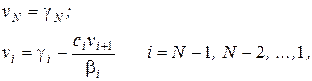
в якому

 |
ПРОГРАМА РОЗРАХУНКІВ
Use MSFLIB
CHARACTER FileDat*10,FileRes*10
F(DIST)=0.0
G0(TIME)=1.0
G1(TIME)=1.0
DIMENSION TOLD(41),TNEW(41),X(41)
DIMENSION A(41),B(41),C(41),D(41),T(41)
READ *,FileDat
OPEN (1,FILE=FileDat)
FileRes=TRIM(FileDat)//'.RES'
OPEN (3,FILE=FileRes)
XMIN=-0.1; YMIN=-0.1; XMAX=1.1; YMAX=1.1
CALL CLEARSCREEN($GCLEARSCREEN)
IN=1; JN=1; IK=1279; JK=799
XZ=(IK-IN)/(XMAX-XMIN)
YZ=(JK-JN)/(YMAX-YMIN)
XYZ=XZ; IF (XZ.GT.YZ) XYZ=YZ
IK=IN+(XMAX-XMIN)*XYZ; JK=JN+(YMAX-YMIN)*XYZ
CALL SETVIEWPORT(IN,JN,IK,JK)
STATUS=SETWINDOW(.TRUE.,XMIN,YMIN,XMAX,YMAX)
Result=setcolorrgb(#ffffff)
CALL LINE_A(XMIN+0.1,0.,XMAX-0.1,0.)
CALL LINE_A(0.,YMIN+0.1,0.,YMAX-0.1)
DO I=1,10
A=FLOAT(I)/10
CALL LINE_A(0.,A,1.,A)
END DO
DO I=1,10
A=FLOAT(I)/10
CALL LINE_A(A,0.,A,1.)
END DO
DTAU=0.00025; TMAX=0.95; M=40; IREQ=100; IPRLT=200;
MP1=M+1; AL=1.0
INTT=M/10; FLOATM=M; DX=1.0/FLOATM;
RATIO=AL*DTAU/(DX*DX)
CONST=1.0-2.0*RATIO
DO I=1,MP1
FLOATI=I
X(I)=(FLOATI-1.0)/FLOATM
TOLD(I)=F(FLOATI*DX)
END DO
TAU=0.0
!WRITE (3,*) TAU,INTT,RATIO,DX,CONST
!WRITE (3,*) (TOLD(I),I=1,MP1,INTT)
ICOUNT=0
1 TAU=TAU+DTAU
ICOUNT=ICOUNT+1
DO I=2,M
TNEW(I)=RATIO*(TOLD(I-1)+TOLD(I+1))+CONST*TOLD(I)
END DO
DO I=1,M
TOLD(I)=TNEW(I)
END DO
TOLD(1)=G0(TAU)
TOLD(MP1)=G1(TAU)
IF ((ICOUNT/IREQ)*IREQ.NE.ICOUNT) GOTO 1
MOVER2=M/2
IF ((ICOUNT/IPRLT)*IPRLT.NE.ICOUNT) GOTO 2
WRITE (3,*) 'TAU=',TAU
WRITE (3,*) (TOLD(I),I=1,MP1)
DO I=1,MP1
CALL CIRCLE(X(I),TOLD(I),0.003)
END DO
CALL LINE(1,MP1,X,TOLD) !; read(*,*)
2 IF (TNEW(MOVER2).LE.TMAX) GOTO 1
WRITE (3,*) X !;STOP
WRITE (3,*) TOLD !; stop
READ (*,*)
C
C Лабораторна робота № 2
C
Result=setcolorrgb(#ff00ff)
DTAU=0.005; TMAX=0.95; M=40; IFREQ=10
FLOATM=M; DX=1.0/FLOATM; RATIO=DTAU/(DX*DX)
DO I=2,M
A(I)=-RATIO; B(I)=1.0+2.0*RATIO; C(I)=-RATIO
END DO
MP1=M+1
DO I=1,MP1
FLOATI=I; T(I)=F(FLOATI*DX)
END DO
TAU=0.0; ICOUNT=0
3 TAU=TAU+DTAU
ICOUNT=ICOUNT+1
T(1)=G0(TAU); T(MP1)=G1(TAU)
DO I=2,M
D(I)=T(I)
END DO
D(2)=D(2)+RATIO*T(1)
D(M)=D(M)+RATIO*T(MP1)
CALL TRIDAG(2,M,A,B,C,D,T)
IF ((ICOUNT/IFREQ)*IFREQ.NE.ICOUNT) GOTO 3
MOVER2=M/2
WRITE (3,*) TAU
WRITE (3,*) (T(I),I=1,MP1)
DO I=1,41
CALL CIRCLE(X(I),T(I),0.007)
END DO
CALL LINE(1,41,X,T)
IF (T(MOVER2).LE.TMAX) GOTO 3
END
SUBROUTINE TRIDAG(II,L,A,B,C,D,V)
DIMENSION A(1),B(1),C(1),D(1),V(1),BETA(101),GAMMA(101)
BETA(II)=B(II)
GAMMA(II)=D(II)/BETA(II)
IIP1=II+1
DO I=IIP1,L
BETA(I)=B(I)-A(I)*C(I-1)/BETA(I-1)
GAMMA(I)=(D(I)-A(I)*GAMMA(I-1))/BETA(I)
END DO
V(L)=GAMMA(L)
LAST=L-II
DO K=1,LAST
I=L-K
V(I)=GAMMA(I)-C(I)*V(I+1)/BETA(I)
END DO
RETURN
END
SUBROUTINE CIRCLE(XCENTRE,YCENTRE,RCIRCLE)
Use MSFLIB
Integer(2) dummy
Real XCENTRE,YCENTRE,RCIRCLE
X1=XCENTRE-RCIRCLE
Y1=YCENTRE+RCIRCLE
X2=XCENTRE+RCIRCLE
Y2=YCENTRE-RCIRCLE
dummy=ELLIPSE_W($GBORDER,X1,Y1,X2,Y2)
RETURN
END
SUBROUTINE LINE(IBEG,IFIN,XX,YY)
Use MSFLIB
DIMENSION XX(98),YY(98)
Integer(2) IS
Real(8) WWX, WWY
Type (WXYCOORD) WXYC
WWX=XX(IBEG); WWY=YY(IBEG)
Call MoveTo_W (WWX,WWY,WXYC)
DO I=IBEG+1,IFIN
WWX=XX(I); WWY=YY(I)
Is=LineTo_W(WWX,WWY)
END DO
RETURN
END
SUBROUTINE LINE_A(XXN,YYN,XXK,YYK)
Use MSFLIB
Integer(2) IS
Real(8) WWX, WWY
Type (WXYCOORD) WXYC
WWX=XXN; WWY=YYN
Call MoveTo_W (WWX,WWY,WXYC)
WWX=XXK; WWY=YYK; Is=LineTo_W(WWX,WWY)
RETURN
END
SUBROUTINE LINE_TO(XXK,YYK)
Use MSFLIB
Integer(2) IS
Real(8) WWX, WWY
Type (WXYCOORD) WXYC
WWX=XXK; WWY=YYK; Is=LineTo_W(WWX,WWY)
RETURN
END
SUBROUTINE MOVE(XXN,YYN)
Use MSFLIB
Integer(2) IS
Real(8) WWX, WWY
Type (WXYCOORD) WXYC
WWX=XXN; WWY=YYN
Call MoveTo_W (WWX,WWY,WXYC)
RETURN
END