Главная | Обратная связь

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ЗАДАНИЯ

ВВЕДЕНИЕ

Все задачи начертательной геометрии следует решать в определенной последовательности: вначале (первый этап) проводится строгое логическое основанное на геометрических закономерностях, пространственное (стереометрическое) решение, при котором выясняется «что?», в какой после­довательности надо делать, и лишь затем (второй этап) решается вопрос о том, «как?» выполнить строго графи­чески составленный стереометрический план.

В первых разделах лекционного курса было показано, как начертательная геометрия, используя свой метод, до­статочно успешно решает многие пространственные задачи. В этот начальный период изучения данной науки главное внимание было уделено вопросам — «что?» надо выполнить для решения конкретной пространственной задачи и «как?» это решение можно выполнить методом начертательной гео­метрии, т. е. графически, на чертеже. При этом не проводи­лась оценка влиянии самого проекционного чертежа на весь последующий ход графического решения.

Однако для графического решения пространственных задач далеко не безразлично, какие изображения объекта - какой проекционный чертеж имеется в нашем распоряжении перед началом решения задачи. Напомню, что величина и форма изображений объекта — его чертеж – зависят от расположения объекта относительно плоскостей проекций.

Известные уже из первых разделов курса задачи показывают, что проекции пространственных объектов, произвольно расположенных относительно плоскостей проекции, не всегда удобны для решения той или иной задачи, так как в ряде случаев имеет место искажение в проекциях натураль­ных форм и размеров проецируемых объектов.

Поэтому желательно для более простого решения задач преобразовать чертеж так, чтобы получить либо вырожденные проекции некоторых элементов, либо их натуральные величины.

Данное задание предназначается для отработки и закре­пления студентами определенных навыков в применении методов, которые дают возможность переходить от общих положений объекта (точек, прямых линий, плоскостей и др.), относительно плоскостей проекций, к частным.

Способы преобразования проекций можно разделить на две группы:

в одной из которых частное положение достигается пере­мещением самого объекта при неизмененном положении за­данной системы плоскостей проекций;

в другой — наоборот - предмет остается неподвижным в пространстве, а изменяется положение плоскостей проек­ций заданной системы (или изменяется направление проеци­рования) так, чтобы после этого предмет оказался в частном положении относительно соответствующей системы взаимно перпендикулярных плоскостей проекций.

К первой группе относятся все способы вращения: вращение вокруг проецирующей прямой; вращение вокруг линии - «способ совмещения»; вращение без указания оси вращения — плоскопараллельное движение.

Ко второй группе относятся: метод замены (перемены) плоскостей проекций и метод дополнительного проецирования.

Все эти преобразования позволяют получить желаемое (целесообразное) расположение предмета относительно пло­скостей проекций.

Большое разнообразие способов преобразования проекций использовать именно тот способ, который приведет к рациональному решению (выполненному при наименьшем количестве линий построения, а, следовательно, более простое и точное) конкретно поставлен­ной задачи.

Правильный выбор решения зависит от того, насколько хорошо усвоен изучаемый материал. Предлагать какие-либо рецепты для решения отдельных задач на наш взгляд бессмысленно из-за огромного количества задач и даже вредно с педагогической точки зрения. Но в качестве общей реко­мендации можно сказать, что:

а) способы вращения целесообразно применять при решениях, связанных с единичным и простым объектом — например, определение истинной величины плоской фигуры; изменение положения точки прямой в пространстве; выполнение планиметрических построений в заданных плоскостях общего положения и т. п.;

б) способы перемены плоскостей проекций целесообразно использовать в тех случаях, когда в условие задачи входят два и более объекта или объект сложной формы — напри­мер, определение расстояния от точки до плоскости; построение плоскости, параллельной заданной, на заданном расстоя­нии; определение кратчайшего расстояния между скрещивающимися прямыми; определение величины параллельных отрезков и расстояний между ними (ребра призмы); постро­ение линии пересечения поверхностей и т. п. Целесообраз­ность применения способа перемены плоскостей проекций для указанного типа задач состоит в том, что заданные объекты остаются в неизменном положении, а перемещается в прост­ранстве лишь один весьма простой и чрезвычайно просто изображающийся объект — плоскость проекций. Перемеще­ние плоскостей проекций может быть осуществлено последо­вательно несколько раз (в зависимости от содержания зада­чи), но каждый раз в системе двух взаимно перпендикуляр­ных плоскостей заменяется лишь одна из них.

В заключение необходимо напомнить, что многие задачи допускают несколько вариантов решения. Но не следует ду­мать, что при этом надо обязательно использовать способы преобразования проекций. Их применяют лишь в тех случа­ях, когда они упрощают решение.

 

СОДЕРЖАНИЕ ЗАДАНИЯ

 

В данном задании требуется решить несколько задач:

Задача № 1. В соответствии с индивидуальным вариан­том, выданным студенту преподавателем, по указанным ко­ординатам построить горизонтальную и фронтальную проек­ции точек А; В; С и D; приняв эти точки за вершины тетра­эдра (четырехгранника), определить видимость его ребер. Указать оси координат.

Примечание. Координаты точек указаны применительно к прямоугольным декартовым координатным осям с единицей измерения по осям 1 мм.

Задача № 2. Определить угол наклона одной из граней тетраэдра (по выбору студента) к плоскости проекций.

Задачу рекомендуется выполнить на безосном чертеже способом вращения вокруг проецирующей прямой i. (Студенты вечернего отделения эту задачу не выполняют).

Задача № 3. Определить величину двугранного угла ABCD при ребре ВС. Повернуть треугольник АВС вокруг стороны ВС на угол ψ ( угол ψ выбрать самостоятельно в пределах от 15° до 60°). На гранях нанести стороны того ли­нейного угла, которым измеряется двугранный. (Студенты вечернего отделения поворот грани не выполняют).

Задачу рекомендуется выполнить на безосном чертеже способом плоскопараллельного перемещения.

Задача № 4. Определить действительную величину одной из граней тетраэдра вращением грани вокруг ее линии уров­ня (h или f).

Задачу выполнить на безосном чертеже.

Задача № 5. Пользуясь способом перемены плоскостей проекций, определить действительную длину кратчайшего расстояния между двумя скрещивающимися ребрами тетра­эдра.

Примечание. Ребра выбираются с учетом наиболее удобного размещения соответствующих построении на отведенной площади задан­ного формата.

Задача № 6. Определить действительную длину расстоя­ния от любой из вершин тетраэдра до противоположной грани, используя способ перемены плоскостей проекций.

Задача № 7. Построить плоскость ∑, параллельную плоскости Δ, которая определяется выбранным в задаче № 4 треугольником, и отстоящую от нее на заданном расстоянии l.

Примечание. Длина отрезка l выбирается в пределах от 10 мм до 30 мм в зависимости от удобства расположения построений на соот­ветствующей площади заданного формата.

Задачи № 6 и № 7 выполняются на одном чертеже.

 

ОФОРМЛЕНИЕ ЗАДАНИЯ

 

Рекомендуемые приемы решения задач данного задания продиктованы учебным характером задания: для закрепления пройденного материала. Не следует думать, что эти задачи можно и нужно решать только так, как рекомендуется в данном задании.

Задание выполняется на листе чертежной бумаги форматом А2. Основная надпись (штамп) с таблицей состава располагается на большей линии рамки чертежа (ГОСТ 2.104-68, форма 1).

Задача № 1. размешается в верхнем левом углу поля чертежа, а все остальные задачи – в любом месте с учётом наиболее удобного размещения соответствующих построений. Примерное расположение задач показано на образцовом листе задания, вывешенном для обозрения в коридоре кафедры.

Все задачи (кроме 6 и 7) выполняются на отдельных чертежах, около которых в кружке диаметра 10 мм указывается номер задачи.

В основной надписи указывается название задания «Способы преобразования проекций».

После полного выполнения задания оно должно быть представлено на проверку преподавателю группы. Линии видимого контура рекомендуется проводить толщиной мм; оси проекций и вспомогательные линии — и т. п.— толщиной s/2; линии связи s/З. Линии связи проек­ций точек заданных элементов желательно проводить с раз­рывом, чтобы не затемнять чертежа.

Результаты выполненных построений в задачах 3; 5; 6 и 7 должны быть указаны в исходных проекциях.

 

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ ЗАДАНИЯ

 

Задача № 1. Построение тетраэдра.Построив по задан­ным координатам точки А, В, С и D, соединим их отрезками прямых. Получен тетраэдр (рис. 1).

Чтобы чертежи были по возможности более наглядными, линии проводят различного типа: видимые элементы изобра­жают сплошными линиями толщиной s, невидимые штриховыми толщиной s/2. При этом видимыми считаются элементы, находящиеся по одну сторону с наблюдателем относи­тельно плоскости (поверхности), в направлении проецирова­ния и невидимыми — находящиеся по разные стороны.

Надо обязательно помнить, что видимость определяется относительно «чего-то». При этом следует рассуждать так: «Определяем видимость относительно плоскости П₁. (или взгляде на плоскость П₁)», «Определяем видимость относи­тельно плоскости П₂» и т. п. Границей видимости является общий элемент — точка встречи прямой с плоскостью (линии с поверхностью) и линия пересечения плоскостей (поверхностей).

Определение видимости относится к объектам, находя­щимся в первом квадранте пространства. (Перемещение объекта в первый квадрант легко осуществляется параллельным переносом).

 

Видимость таких объектов, как прямая и кривая линии, плоскость и кривая поверхность, можно определить с помощью наиболее простых геометрических элемен­тов – отдельных точек этих объектов.

Например, в данной задаче при определении относительно плоскости П₁ надо выяснить: какое ребро - АС или BD закрыто от наблюдателя гранями тетраэдра. В связи с тем, что ребра АС и BD являются прямыми линиями для анализа видимости достаточно выбрать по одной точке на каждом из ребер. В качестве таких точек взяты точки М и N; ; . Прежде всего обратите внимание на то, что точки М и N (рис. 2) лежат на одном горизонтально-проецирующем луче (на одном «зрительном» луче). Такой выбор точек в данной ситуации не случаен: точки, лежащие на одном проецирующем луче, имеют постоянными те параметры, которые не интересуют нас при соответствующем анализе. В данном случае нам надо узнать взаимное расположение точек М и N относительно плоскости П₁ т. е, их высоты, поэтому необходимо иметь для них одинаковыми глубины и широты (т. е. расстояния до плоскостей П₁ и П₃). Кроме того, такие точки легко и удобно выбрать с помощью соответствующих им совпадающих проекций в данном случае горизонтальных. Точки, лежащие на одном проецирующем луче, называются конкурирующими. Поэтому говорят, что определение видимости основано на методе конкурирующих точек.

Итак, на основании предварительных замечаний процесс определения видимости сводится к следующему. Для определения видимости ребер АС и BD относительно плоскости П₁ выбираем точки М и N, воспользовавшись для этого их горизонтальными проекциями (М₁ и N₁). Взаимное расположение точек М и N относительно плоскости П₁ отчетливо видно по расположению фронтальных проекций этих точек (M₂ и N₂). В данном примере точка N ближе к наблюдателю, чем точка М. Следовательно, N закроет М, т.е. её точка N видима относительно плоскости П₁. Точка N принадлежит прямой BD следовательно, BD видима и ее горизонтальная проекция B₁D₁ изображается сплошной линией толщиной s, а АС — невидима и ее горизонтальная проекция А₁С₁ изображается штриховой линией (рис. 2). Аналогичным образом определяется видимость относительно других плоскостей проекций.

Очерки (проекция видимого контура поверхности применительно данной плоскости проекций) изображений тетраэдра проводятся толщиной s.

Совершенно очевидно, что чертеж на рис.2 читается значительно проще благодаря своей наглядности, чем чертеж на рис.1.

Все построения и обозначения, связанные с определением видимости, должны быть сохранены на чертеже.

Задача №2. Определение угла наклона плоскости отно­сительно плоскости проекций П₁. Будем рассуждать так. Плоскость общего положения (грань тетраэдра) образует с плоскостью проекций или, что то же — с плоскостью, парал­лельной плоскости проекций (плоскостью уровня) — дву­гранный угол, величина которого равна углу наклона плос­кости, ибо плоскость проекций и плоскость уровня плоскость уровня - плоскости нулевого наклона. Ребром этого двугранного угла явля­ется след плоскости на плоскости проекций или линия уровня плоскости, т. е. линия пересечения плоскости с плоскостью проекций или с плоскостью уровня.

Величина двугранного угла, как известно, определяется линейным углом со сторонами, перпендикулярными ребру двугранного угла — в данном случае перпендикулярными следу плоскости или соответствующей линии уровня плоско­сти.

Так как одна из сторон этого линейного угла параллельна плоскости проекций, то его величина равна углу наклона к плоскости проекций другой его стороны. Очевидно, что такие линии плоскости (и линии им параллельные) имеют наиболь­ший угол наклона к соответствующей плоскости проекций (по сравнению с другими линиями плоскости). Такие линии плоскости называются линиями наибольшего наклона (линии наибольшего наклона относительно плоскости П₁ называются линиями наибольшего ската).

Следовательно, угол наклона плоскости можно определить с помощью более простого геометрического элемента — прямой линии, а именно с помощью линии наибольшего ската.

Построение линий наибольшего наклона основывается на их перпендикулярности соответствующим линиям уровня плоскости. Так, для

построения линии наибольшего ската плоскости надо провести горизонталь этой плоскости - линия, проведенная перпендикулярно к ней, и будет линией наибольшего наклона относительно плоскости П₁.

Проведем горизонталь из точки С, а к ней линию наибольшего ската из точки А. На комплексном чертеже эти построения выполняются достаточно просто на основании теоремы о прямом угле: горизонтальная проекция , линии наибольшего ската AM перпендикуляра горизонтальной проекции С₁K₁ горизонтали; затем по обычным правилам строится, фронтальная проекция А₂М₂.

Однако, хотя мы и имеем линию наибольшего ската, ве­личина угла ее наклона относительно плоскости П₁ еще не найдена, ибо эта прямая не параллельна плоскости проекций П₂. Преобразование AM в желательное для данной задачи положение в данном случае целесообразно выполнить методом вращения вокруг проецирующей прямой. Для упрощения построений ось вращения i, перпендикулярную плоскости П₁ проведем через точку А. В этом случае все

преобразование сведется к перемещению лишь одной точки прямой, например, точки М. Все точки прямой опишут в пространстве окружности, перпендикулярные оси вращения i, а следовательно, параллельные плоскости проекций П₁, на которую и изобразятся в натуральную величину. Фронтальные проекции этих окружностей представляют собой прямые, перпендикулярные линиям связи.

При данном, вращении угол наклона прямой (или плоско­сти) относительно соответствующей плоскости проекции (в нашем примере — относительно плоскости П₁) остается неизменным. А следовательно, не изменяется величина и форма проекции: угол же наклона относительно другой плоскости проекций изменяется. Сочетание этих факторов и позволяет достаточно просто решить многие позиционные и метрические задачи. Так в нашем примере надо, чтобы прямая AM стала параллельной плоскости П₂. Графически фиксацию этого по­ложения осуществляют с помощью горизонтальной проекции , располагая ее перпендикулярно линиям связи. После построения фронтальной проекции получим ответ на поставленную задачу.

При этом с помощью чертежа надо рассуждать так: если горизонтальная проекция отрезка перпендикулярна линиям связи, то значит сам отрезок параллелен плоскости проекций П₂, а, следовательно на данную плоскость длина отрезка ( ) и угол его наклона относительно плоскости П₁ проецируются в действительную величину.

Задача решена. Но кроме этого, лишь в учебных целях, надо этим же методом вращения преобразовать положение и вместе с его линией наибольшего ската AM. Очевидно, что когда AM займет положение линии фронтального уровня (фронтали), горизонталь СК плоскости окажется в положении фронтально-проецирующей прямой, а следовательно сама плоскость станет перпендикулярной плоскости проекций П₂ (совпадает с направлением прое­цирования). Проверкой правильности выполненных построений будет служить выродившаяся в прямую линию
фронтальная проекция: ( ) плоскости . (Горизонталь­ные проекции и - идентичные по своей форме и размерам.

Задача № 3. Определение величины двугранного угла. Угол между двумя плоскостями (двугранный) измеряется линейным углом, составленным прямыми пересечения граней с плоскостью, перпендикулярной ребру двугранного угла.

Линейный угол, служащий мерой двугранного угла, изобразится без искажения на плоскость проекций, перпендикулярную ребру двугранного угла. Однако в большинстве случаев ребро двугранного угла занимает общее положение относительно плоскостей проекций. В частое (проецирующее) положение ребро двугранного угла можно привести различными преобразованиями. В данном задании эту задачу требуется выполнить, используя способ плоскопараллельного перемещения.

Такое перемещение, при котором все точки геометрической фигуры движутся по плоским траекториям, параллельным одной из плоскостей проекций, без указания оси вращения, называется плоскопараллельным.

В предыдущей задаче данного задания, при вращении треугольника АВС вокруг оси i, перпендикулярно П₁, все точки фигуры перемешались по плоским траекториям (окружностям) параллельным плоскости П₁. Ничто не изменилось бы в конечном результате, если бы точки треугольника из первого положения АВС переместились в новое положение не по окружности, а по каким-либо другим плоским линиям без изменения углов наклона фигуры к пло­скости П₁. В этом случае разность высот любых двух точек фигуры треугольника оставалась бы неизменной, а, следовательно, не изменилась бы величина и форма горизонтальной проекции.

Прежде, чем решать задачу на определение величины двугранного угла, рассмотрим более простей пример: преоб­разуем отрезок прямой ВС общего положения в горизонтальнопроецирующий, используя плоскопараллельное перемеще­ние. Эту задачу можно выполнить двукратным преобразова­нием (рис. 4): вначале отрезок ВС располагают параллельно одной плоскости проекций, например, параллельно плоско­сти П₂, а затем делают его перпендикулярным другой плос­кости проекций — плоскости П₁.

При плоскопараллельном перемещении характер плоских траекторий точек безразличен и поэтому на чертежах изобра­жают только соответствующие проекции плоскостей уровня, в которых перемещаются точки, а не проекции траекторий точек. Так точка В и С перемещаются соответственно в го­ризонтальных плоскостях Г¹ и Г². Горизонтальные проекции этих плоскостей совпадают с полем П₁ и не обозначаются, а фронтальные проекции изображаются прямыми Р¹₂ и Г²₂, перпендикулярными линиями связи.

Величина горизонтальной проекции В₁С₁ отрезка ВС при сто перемещении в новое положение В₁С₁ остается неизмен­ной ( ), так как при перемещении не изменяется наклон отрезка ВС к плоскости П₁. Новая проекция В₁С₁ от­резка может быть изображена в любом свободном месте чертежа. Но для того, чтобы отрезок ВС сделать параллельным плоскости П₂, горизонтальная проекция В₁С₁ должна быть направлена перпендикулярно линиям связи.

Построив новую горизонтальную проекцию отрезка, находим новые фронтальные проекции В₂С₂ точек В и С пе­ремещенного отрезка при помощи линий связи на фронталь­ных проекциях плоскостей перемещения Г₂¹ и Г²₂, ( На этом этапе заканчивается решение задачи на определение дейст­вительной величины отрезка прямой, так как ( ).

Затем перемещаем отрезок ВС в плоскости Ф до положе­ния, перпендикулярного плоскости П₁. При этом фронталь­ная проекция должна занять положение, параллельное линиям связи, а горизонтальная проекция выродится в точку .

Плоскопараллельное перемещение является общим слу­чаем приема вращения вокруг оси, перпендикулярной плос­кости проекций. Эта ось при плоскопараллельном перемеще­нии не изображается. Но эта ось может быть найдена, так как любое плоское перемещение может быть выполнено вращением вокруг оси. Однако, не указывая ось вращения, можно наиболее удобно размещать проекции фигур на поле чертежа.

Но вернемся к решению задачи № 3. Итак, для определе­ния величины двугранного угла надо привести его ребро в проецирующее положение. Это можно выполнить двукратным применением плоскопараллельного перемещения.

Во-первых, располагаем ребро ВС параллельно плоскос­ти П₂, перемещая точки В и С в плоскостях, параллельных плоскости П₁ (рис. 5). В это же время аналогичным образом перемещаются и все жестко связанные между собой точки фигуры двугранного угла. При этом величина и ферма гори­зонтальной проекции фигуры остаются без изменения . Расположив горизонтальную проекцию ребра перпендикулярно линиям связи, строим новую проекцию всей фигуры двугранного угла. (Построе­ние фигуры 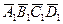равной , удобно выполнить при помощи циркуля — методом засечек).

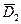Новые фронтальные проекции точек фигуры ( ; ; и ) определяются в пересечении линий связи с соответству­ющими фронтальным проекциями плоскостей перемещения точек.

Затем, перемещая все точки фигуры в плоскостях, парал­лельных плоскости П₂, располагаем ребро ВС перпендику­лярно плоскости П₁. В этом случае фронтальная проекция ребра ВС займет положение, параллельное линиям свя­зи. Горизонтальные проекции траекторий точек изобразятся в виде прямых, перпендикулярных линиям связи.

Линейный угол, которым измеряется двугранный, можно изобразить в любом месте фигуры двугранного угла. В на­шем примере (рис. 5), сторона DE проведена через верши­ну D ( ). Затем, построив фронтальную проекцию этого угла, с помощью линий связи определяем гори­зонтальную проекцию . Используя аналогичный прием, строим горизонтальную проекцию угла, а после этого — фронтальную проекцию .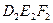

Остается выполнить последнее требование задачи № 3: повернуть грань ABC вокруг ребра ВС на угол φ. Выполне­ние этих построений следует начинать на горизонтальной проекции , т. е. там, где угол проецируется в дейст­вительную величину. Определив положение А¹₁ вершины А¹ после поворота, находят уже известным приемом все осталь­ные проекции (А¹₂; ; , ) вершины А¹.