Главная | Обратная связь

Задача № 4. Определение величины плоской фигуры.

Плоская фигура проецируется без искажения на плоскость, ей параллельную. Поэтому для графического определения величины плоской фигуры общего положения желательно эту фигуру привести в положение, параллельное одной из плоскостей проекций. В это частное положение плоскую фигуру общего положения можно привести несколькими при­емами, например:

а) вращением плоской фигуры вокруг осей, перпендику­лярных плоскостям проекций;

б) плоскопараллельным перемещением;

в) способом замены плоскостей проекций.

Все перечисленные методы позволяют осуществить пере­вод плоской фигуры общего положения в параллельное пло­скости проекций двойным преобразованием: вначале фигура должна занять проецирующее (перпендикулярное) положе­ние относительно одной плоскости проекций, а затем уже-параллельное другой плоскости проекций.

Однако существует еще один способ, позволяющий преоб­разовать плоскую фигуру в положение плоскости уровня ра­зовым перемещением: вращением плоской фигуры вокруг одной из принадлежащих ей прямых линий уровня (горизон­тали или фронтали).

Преимущество этого метода при решении данной задачи состоит еще и в том, что преобразование всей плоской фигуры в желаемое положение уровня осуществляется путем перемещения лишь одной точки этой фигуры.

Действительно, проведя в плоской фигуре линию уровня, например, горизонталь, и приняв се за ось вращения, доста­точно перевести вращением в этот уровень одну из точек фигуры. В этом случае вся плоскость окажется в положении, параллельном плоскости проекций. Останется выполнить лишь необходимые несложные построения всей фигуры при новом ее положении.

Рассмотрим вопрос о том, как осуществляется вращение точки вокруг линии уровня и как это выполняется графичес­ки на комплексном чертеже.

В качестве оси вращения возьмем горизонталь СК и вне ее точку В (рис. 6). При вращении вокруг горизонтали точ­ка В будет перемещаться по окружности, находящейся в плоскости Σ перпендикулярной оси вращения СК. Так как СК||П₁ то плоскость вращения 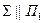т. е. Σ — горизонталь­но-проецирующая плоскость.

Плоскость Σ пересечет ось вращения — горизонталь СК в точке О, являющейся центром вращения точки В. Отрезок ОВ представляет собой радиус вращения точки В. Очевидно, что радиус вращения ОВ перпендикулярен оси вращения СК.

Плоскость Σ, а, следовательно, и окружность, по которой перемещается точка В, изобразится на плоскость П₁ в виде прямой Σ₁, перпендикулярной горизонтальной проекции гори­зонтали СК ( ) - на основании теоремы о прямом угле: если и то и .

Предположим, что требуется переместить точку В до уровня горизонтали СК. В этом случае радиус вращения ОВ расположится параллельно плоскости проекций П₁ и, следо­вательно, изобразится на эту плоскость в натуральную величину.

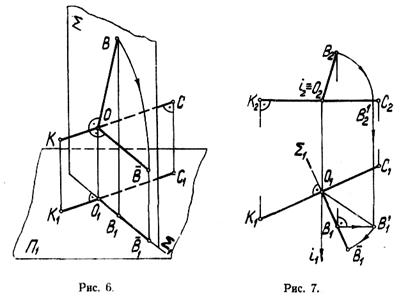
В связи с этим на комплексном чертеже (рис. 7) новое (искомое) положение В₁ точки В может быть найдено, если на горизонтальной проекции Σ₁ плоскости Σ отложить от центра вращения О действительную величину радиуса вра­щения ОВ.

Величину радиуса вращения на комплексном чертеже можно найти одним из методов, например, методом вращения вокруг проецирующей оси, в данном примере (рис. 7) — во­круг оси перпендикулярной плоскости П₂ и приходящей через точку О. Новое положение В₁ точки В вместе с неподвижной горизонталью СК определяют собой положение плоскости, параллельной плоскости П₁.

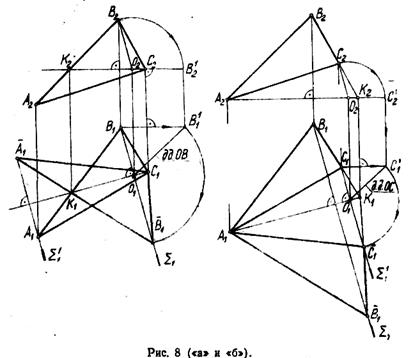
Вернемся к задаче на определение величины одной из граней тетраэдра ABCD, например, грани ABC.

На рис. 8 («а» и «б») представлены два варианта графи­ческого решения этой задачи: вращение треугольника осуще­ствлено вокруг внутренней горизонтали СК и внешней гори­зонтали АК. (В задании надо выполнить один из этих вари­антов: если имеется достаточно свободной площади на поле чертежа, то желательно решение выполнить по варианту «б»; если надо получить более компактный чертеж, то решение следует выполнять по варианту «а»).

При вращении вокруг горизонтали все точки треугольни­ка будут описывать окружности в плоскостях, перпендику­лярных оси вращения СК. или АК.

Так как одна вершина треугольника, находясь на оси вра­щения, остается неподвижной, то надо построить новые поло­жения двух других вершин. Новое положение вершины В построено так, как было выполнено на рис. 7. Новое положе­ние 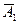точки А, вращающейся в своей горизонтально-проецирующей плоскости Σ₁ (рис. 8«а»), может быть найдено ана­логично. Но так как точка К принадлежит прямой ВК, то решение упрощается. Точка К неподвижна, а новое положение точки В известно. Поэтому на чертеже достаточно прове­сти через проекции и этих точек прямую и в ее пересе­чении с горизонтальной проекцией Σ₁¹ плоскости вращения точки А найти проекцию . Проекция будет искомой про­екцией точки А в ее новом положении , которое займет точ­ка А при приведении треугольника в положение, параллель­ное горизонтальной плоскости проекций. Аналогичным обра­зом находится новое положение точки С (рис.8«б»).

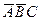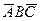В полученных положениях и плоскость тре­угольника параллельна горизонтальной плоскости проекций и, следовательно, треугольник проецируется на нее без искаже­ния, т. е. величина проекций и представляет величину самого треугольника ABC. Очевидно, что и углы при вершинах треугольника проецируются на горизонтальную плоскость без искажения. Поэтому для нахождения углов между пересекающимися прямыми можно применять этот же способ вращения плоскости вокруг одной из ее линий уровня до положения, параллельного одной из плоскостей проекций.

Заданную плоскость треугольника можно расположить и параллельно фронтальной плоскости проекции П₂ вращением вокруг фронтали. План решения при этом аналогичен рас­смотренному и поэтому рекомендуется выполнить эти постро­ения самостоятельно.

Задача № 5. Определение кратчайшего расстояния между скрещивающимися прямыми. Кратчайшим расстоянием меж­ду скрещивающимися прямыми является отрезок общего перпендикуляра к ним.

Для решения этой задачи с помощью комплексного черте­жа целесообразно одну из скрещивающихся прямых привести в проецирующее положение (не нарушая взаимного расположения этих прямых). Тогда искомый отрезок перпендикуля­ра между двумя скрещивающимися прямыми изобразится без искажения на соответствующую плоскость проекций (рис. 9): в данном примере отрезок MN, будучи перпендику­ляром к ВС, является параллельным плоскости П₁ а, следо­вательно, изобразится на П₁ в истинную величину.

Для того, чтобы прямую общего положения, привести в проецирующее положение, т. е., чтобы, зафиксировать част­ные значения двух углов наклона (0° по отношению к одной плоско­сти проекций и 90°— по отношению к другой плоскости проекций), не­обходимо выполнить двойное пре­образование: вначале преобразо­вать прямую в положение, парал­лельное относительно одной плос­кости проекций, а затем — проеци­рующее (перпендикулярное) поло­жение относительно другой плоско­сти проекций.

Такие преобразования возмож­но выполнить как одним из спосо­бов вращения, так и способом заме­ны плоскостей проекций. Однако, в связи с тем, что в нашей задаче заданы две прямые, методы враще­ния потребуют достаточно сложных графических построений, так как перемещая одну прямую, мы обя­заны на такой же угол повернуть и другую прямую. И все это надо выполнить дважды.

Значительно проще прямую общего положения привести в проецирующее положение способом замены плоскостей про­екций (рис. 11), ибо в этом случае надо переместить в про­странстве хотя и два раза, но один объект — плоскость про­екций. Кроме этого плоскости проекций очень просто изоб­ражаются на комплексном чертеже — одна из проекций этих плоскостей вырождается в прямую линию — ось проекций.

Способ замены плоскостей проекций состоит в том, что одна из двух плоскостей проекций заменяется новой плоско­стью нужным образом расположенной относительно объекта; при этом новая плоскость должна быть перпендикулярной к оставшейся (неизменяемой) плоскости проекций.

В качестве примера, иллюстрирующего способ замены плоскостей проекций, рассмотрим задачу на определение ве­личины отрезка АВ (рис. 10): взамен П₂ следует выбрать новую вертикальную плоскость проекций и парал­лельную отрезку АВ.

При этом взаиморасположение отрезка и неизменной пло­скости проекций П₁ не изменится, а значит, не изменяется и высоты и разнести высот всех точек отрезка АВ от П₁. На­пример, если высота точки А равна величине 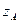и изобра­жается на П₂ отрезком , то и на плоскости П₄ она будет изображаться таким же отрезком 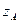, так как отсчет высоты производится от одной и той же плоскости П₁. Вы­соты точек А и В на новой плоскости проекций П₄ изобра­жаются расстояниями от новой оси до новых проекций и точек А и В, равными расстояниями от заменяемой оси до заменяемых проекций А₂ и В₂ тех же точек.

На комплексном чертеже параллельность отрезка АВ и плоскости П₄ отражается параллельностью их горизонталь­ных проекций .

Новые плоскости проекций, а следовательно, и новые оси проекций можно выбрать наиболее удобно для отсчетов рас­стояний и рационального использования поля чертежа, но всегда перпендикулярно линиям связи данной системы. Если объект первоначально был задан на безосном чертеже, то ось проекций следует выбрать самостоятельно, с учетом вы­шеизложенных рекомендаций.

Комплексный чертеж задачи на преобразование прямой общего положения в проецирующую прямую приведен на рис. 11. Так как плоскость проекций П₁ не заменяется, то на комплексном чертеже проекций A₁B₁ остается горизон­тальной проекцией отрезка и в новой системе плоскостей .

Для построения новой вертикальной (на П₄) проекции отрезка — через проекции А₁ и В₁ его точек А и В перпенди­кулярно проекции А₁В₁ или, то же самое, новой оси х₁₄ про­ведены линии связи. Разность расстояний z_А - z_В точек А и В от оставшейся плоскости проекций в новой системе будет равна соответственно разности тех же расстоянии в системе . Полученная величина проекций А₄В₄ на П₄ равна АВ, так как отрезок АВ параллелен плоскости проек­ций П₄.

Если же по условию задачи отрезок требуется преобра­зовать в проецирующее положение, то выбирают еще одну плоскость проекций (П₅), считая систему исходной системой плоскостей проекций. Для этого новую плоскость проекций П₅ располагают перпендикулярно отрезку АВ и плоскости П₄. На чертеже это выражается перпендикуляр­ным расположением оси х₄₅ к вертикальной проекции А₄В₄ отрезка АВ. В новой системе плоскостей проекций отрезок АВ совпадает с направлением проецирующего луча к плоскости П₅ и его проекций на П₅ вырождается в точку .

Если надо получить более компактный чертеж, то новую плоскость проекций следует расположить так, как располо­жена плоскость П¹₅ (рис. 11).

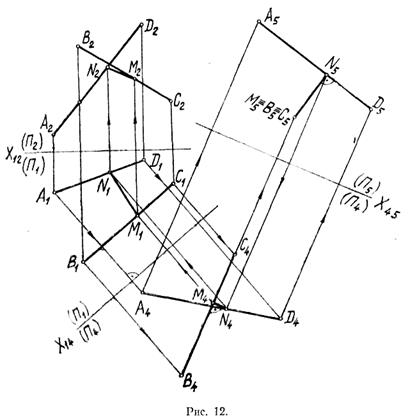
На рис. 12 приведено решение задачи по определению кратчайшего расстояния между двумя скрещивающимися прямыми AD и СВ.

Новая плоскость проекций П₄ выбрана параллельной от­резку ВС ( ). После построения новых вертикальных проекций отрезков A₄D₄ и В₄С₄ выбирается плоскость и перпендикулярная отрезку ВС ( ).

После нахождения проекций A₅D₅ и В₅С₅ строится проек­ция M₅N₅ отрезка MN, которая проводится через перпендикулярно проекции A₅D₅ (на основании теоремы о взаимно перпендикулярных прямых). Получив проекцию M₅N₅, которая является истинной величиной отрезка MN, следует построить проекции отрезка на всех предыдущих плоскостях проекций. Для этого поступаем так: проведя ли­нию связи из N₅, находим проекцию N₄; проекция N₄M₄ рас­полагается перпендикулярно В₄С₄, так как отрезок ВС па­раллелен плоскости проекции П₄; затем, используя правило инцидентности точек и прямых, с помощью линий связи на­ходим проекции М₁; N₁; М₂ и N₂ точек М и N. Эти обратные построения могут служить проверкой выполненных построе­ний: ни одна из проекций — M₄N₄; M₁N₁ M₂N₂ — не может быть больше проекции M₅N₅ = MN.

Две скрещивающихся прямых определяют одну единст­венную пару параллельных плоскостей. Поэтому кратчайшее расстояние между двумя скрещивающимися прямыми есть в то же время и расстояние между проходящими через них параллельными плоскостями и, следовательно, может быть определено как расстояние между параллельными плоско­стями.

Задача № 6. Определение расстояния от точки до плоско­сти.Расстояние от точки плоскости измеряется отрезком перпендикуляра от точки до этой плоскости.

Решение данной задачи состоит из трех последовательных операций: 1) проведение перпендикуляра из данной точки на заданную плоскость; 2) определение точки встречи перпендикуляра с плоскостью; 3) определение истинной величины отрезка (между заданной точкой и точкой встречи).

Как известно, прямая перпендикулярна к плоскости, если она перпендикулярна двум непараллельным прямым плоско­сти.

Пусть требуется через точку А провести прямую АЕ, пер­пендикулярную плоскости треугольника BCD (рис. 13). При графическом (на комплексном чертеже) построении перпен­дикуляра к плоскости мы вынуждены в качестве двух прямых брать линии уровня плоскости (горизонталь и фронталь), ибо только в этом случае прямой угол между перпендикуляром АЕ и линиями уровня (СК и BL) изобразится на соответст­вующих плоскостях проекций без искажения. Так фронталь­ная проекция А₂Е₂ пройдет под прямым углом к фронталь­ной проекции С₂К₂ фронтали СК, а горизонтальная проек­ция А₁Е₁ — под углом 90° к горизонтальной проекции B₁L₁ горизонтали BL. Так как фронталь СК и горизонталь BL были выбраны произвольно, то прямая АЕ в общем случае не пересекается, а скрещивается с ними.

Итак, А₁Е₁ и А₂Е₂ — проекции одной и той же прямой АЕ, перпендикулярной двум прямым плоскости ( и ). Следовательно, .

Таким образом, можно сформулировать следующий вы­вод: если в пространстве прямая перпендикулярна плоскости, то на комплексном чертеже фронтальная проекция прямой перпендикулярна фронтальной проекции фронтали данной плоскости, а горизонтальная проекция прямой перпендику­лярна горизонтальной проекции горизонтали этой плоскости. Справедливо и обратное утверждение.

Переходим ко второму этапу задачи — определению точки встречи прямой с плоскостью (в данном примере — пря­мой АЕ с плоскостью треугольника BCD).

Построение точки встречи прямой с плоскостью является одной из основных позиционных задач курса. Она входит как вспомогательная задача в решение многих более слож­ных задач, как например, задачи на взаимное пересечение поверхностей, пересечение поверхностей плоскостью или, как в данном случае — определение расстояния между точкой и плоскостью. Поэтому необходимо особо остановится на зада­че по определению точки встречи прямой с плоскостью,

Напомню, что могут быть два случая взаимного располо­жения прямой и плоскости: прямая или принадлежит плос­кости или пересекает ее. Если прямая не принадлежит плос­кости, то она пересекает плоскость в единственной точке. При этом пересечение может быть в собственной (доступной) точ­ке, если прямая располагается относительно плоскости под произвольным углом или под углом 90° или в бесконечно уда­ленной (несобственной) точке, если прямая параллельна пло­скости. Расположение прямой под углом 90° (прямая перпен­дикулярна плоскости) и под углом 0° (прямая параллельна плоскости) являются частными случаями взаимного располо­жения прямой и плоскости.

Рассмотрим общий случай — когда прямая пересекает плоскость под произвольным углом.

Для того, чтобы графически (на чертеже) показать, что точка встречи действительно является общей для прямой и плоскости, т. е. чтобы осуществить инцидентность (взаимо­принадлежность) точки и плоскости, необходимо и достаточ­но иметь линию в заданной плоскости Σ, которая пересекала бы заданную прямую АЕ.

Методом последовательного приближения (подбором) указанную вспомогательную линию графически найти не уда­ется.

Поэтому используют такой прием: через заданную прямую

проводят вспомогательную плоскость ( , рис. 14); находят линию (1—2) пересечения плоскостей Σ и , и, на основании того, что линия (1—2) и АЕ находятся в одной плоскости , а, следовательно,— пересекаются, получают точку . Точка S и является точкой общей для заданной прямой АЕ и заданной плоскости Σ, так как она принадлежит АЕ и линии (1—2), находящейся в плоскости Σ.

Таким образом, задача на построение точки встречи пря­мой с плоскостью состоит из трех последовательных операций (рис. 14):

1) введение вспомогательной плоскости , проходящей через заданную прямую АЕ;

2) нахождение линии (1—2) пересечения двух плоскостей — заданной Σ и вспомогательной .

3) определение точки встречи S как точки пересечения линий АЕ и (1—2).

Выполним эти операции при решении задачи на комплекс­ном чертеже (рис. 13). В качестве вспомогательной плоско­сти (Вспомогательные плоскости (поверхности) часто называют посред­никами. Посредники позволяют не только найти вспомогательную линию, но и дают возможность утверждать, что вспомогательная и заданная линии пересекаются, так как они находятся в одной (пусть вспомогатель­ной) плоскости. Подробно о посредниках смотрите методическое пособие «Линии среза и перехода», Савкин Ю. Г.) в большинстве случаев используют проецирующие пло­скости, так как при этом упрощается графическая часть опе­раций по проведению плоскости через прямую и по определе­нию линии пересечения плоскостей. Действительно, проведя фронтально-проецирующую плоскость через прямую АЕ (на чертеже это действие отражается совпадением фронтальных проекций прямой АЕ и плоскости : ), мы без дополнительных построений определяем линию (1—2) пересечения плоскостей Σ (плоскость ) и (вначале фронтальную про­екцию 1₂—2₂, а затем с помощью линий связи и горизонталь­ную проекцию l₁—2₁).

Совпадение фронтальных проекций и а , говорит о том, что линии (1—2) и АЕ принадлежат одной (вспомогательной) плоскости. Пересечение этих линий и даст искомую точку встречи S. Но на фронтальной плоско­сти проекций проекции этой точки пока не видно. Тогда, зная, что если прямые пересекаются, то их одноименные проекции пересекаются в точках, которые являются проекциями точки пересечения прямых, обращаемся к горизонтальным проек­циям прямых. Пересечение горизонтальных проекций и l₁—2₁ и есть горизонтальная проекция S₁ точки встречи S. Проведя линию связи из S₁ до пересечения с фронтальной проекцией А₂Е₂, находим фронтальную проекцию S₂ точки S: точка встречи прямой АЕ с плоскостью Σ найдена .

Остается определить истинную величину отрезка AS, что можно выполнить одним из известных способов, например, методом прямоугольного треугольника.

Однако решение всей задачи на определение кратчайшего расстояния от точки до плоскости выполняется значительно проще, если плоскость занимает частное — проецирующее — положение (рис.15). Действительно, если плоскость , то прямая AS, перпендикулярная , будет параллельна плоскости П₂. Следовательно, фронтальная проекция A₂S₂ перпендикуляра AS изобразится под углом 90° к фронталь­ной проекции плоскости на основании теоремы о прямом угле, а горизонтальная проекция A₁S₁ бу­дет перпендикулярна линиям связи (как горизонтальная про­екция фронтали). Кроме этого, являясь фронталью, отре­зок AS изображается на плоскости П₂ без искажения A₂S₂=AS.

Так как заданная плоскость BCD — фронтально-проеци­рующая, то фронтальные проекции всех точек этой плоскости совпадут с ее фронтальной проекцией B₂C₂D₂. Поэтому фрон­тальная проекция S₂ точки встречи S должна принадлежать фронтальной проекции B₂C₂D₂ плоскости. Одновременно S₂ принадлежит фронтальной проекции A₂S₂ прямой AS. Сле­довательно, S₂=A₂S₂×B₂C₂D₂.

Горизонтальная проекция S₁ точки S находится в пересе­чении линии связи из S₂ с горизонтальной проекцией A₁S₁ прямой AS.

На основании вышеизложенного естественно возникает желание преобразовать плоскость общего положения в прое­цирующую. В данном задании это преобразование предла­гается выполнить способом замены плоскостей проекций.

Для того, чтобы плоскость общего положения стала пер­пендикулярной плоскости проекций, необходимо и достаточ­но, чтобы одна из прямых плоскости расположилась под углом 90° к плоскости проекций.

Если для этой операции взять прямую общего положения (одну из сторон треугольника BCD), то для её преобразования в проецирующее положение потребуется двойное преобразо­вание (например, две замены плоскостей проекций).

Но ничто не мешает взять в плоскости линию частного положения, например, фронталь. В этом случае разовым преобразованием — одной заменой плоскости проекций — линия уровня, а, следовательно, и вся плоскость, могут быть преобразованы в проецирующее положение.

На рис. 16 показан вариант решения задачи на определе­ние расстояния от точки А до плоскости .

Проведя фронталь СК, располагаем новую плоскость проекции П₄, перпендикулярно этой линии ( ). По­строив новые горизонтальные проекции и плоскости BCD и точки А, определяем истинную величину отрезка AS=A₄S₄. Затем обратным проецированием находим фрон­тальную A₂S₂ и горизонтальную A₁S₁, проекции AS.

Задача № 7. Построение плоскости, параллельной задан­ной, на заданном расстоянии.Из геометрии известно, что две плоскости взаимно параллельны, если две непараллельных прямых одной плоскости соответственно параллельны двум прямым другой плоскости.

Очевидно, что на заданном расстоянии от заданной пло­скости можно построить две плоскости, ей параллельные. Для этого надо на перпендикуляре к заданной плоскости отложить указанное расстояние и через полученные точки провести по две пересекающихся прямых, соответственно параллельных двум прямым заданной плоскости.

Построение перпендикуляра к плоскости, как было пока­зано в задаче № 6, удобно выполнить, если плоскость зани­мает проецирующее положение. Решение задачи № 7 выпол­нено на одном чертеже, совместно с решением задачи № 6 (рис. 16). Через точку В проведен перпендикуляр, проекция M₄N₄ которого изображается без искажения. Отложив на перпендикуляре заданное расстояние (в данном примере 15 мм), через точки М и N проводим плоскости Σ¹ и Σ²: на плоскости П₄ они изображаются в виде прямых Σ¹₄ и Σ²₄, а на плоскостях П₂ и П₁ — проекциями двух прямых, соответ­ственно параллельными проекциями двух прямых заданной плоскости.

 

 

Редактор В. И. Лузева Техн. редактер А. А. Капралова

Синю в набор 10.11.87. Подп. в печ. 07.04.88. Форм. бум. 60×84 .

Усл. кр. отт. 1,86. Объем 1,86 усл. п. л. Уч.-изд. л. 1,68. Тираж 1500.

Заказ 1090. Бесплатно.

Типография МИХМ 107884, ГСП-6, Москва, Б-66, ул. К Маркса, 21/4