 |
|
Відкриті транспортні задачі.
При розгляді транспортної задачі (5.1 - 5.4) передбачалася справедливість рівності 
. Такі транспортні задачі називаються закритими (збалансованими). На практиці часто виникають так звані відкриті (незбалансовані) транспортні задачі, для яких 
.
Якщо 
, то задача полягає у відшукуванні найбільш дешевого плану перевезень, при якому повністю задовольняються потреби пунктів призначення Вj (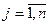 
); при цьому не всі запаси пунктів відправлення вичерпуються.
Якщо ж 
, то потреби пунктів призначення не повністю задовольняються, а запаси пунктів відправлення вичерпуються.
Відкрита транспортна задача зводиться до закритої у такий спосіб.
Нехай . Введемо фіктивний пункт призначення Вn+1 з потребою 
.
Будемо вважати, що cin+1=0 при всіх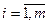 
. Після вирішення отриманої закритої транспортної задачі опустимо перевезення в пункт Вn+1; одержимо оптимальний план перевезень для відкритої транспортної задачі.
Аналогічно, у випадку справедливості нерівності вводиться фіктивний пункт відправлення Аm+1, і справа зводиться до вирішення закритої транспортної задачі.
Приклад. Нехай вихідні дані наведені в таблиці 5.12
Таблиця 5.12
| Пп Пв | В1 | В2 | В3 | Запаси |
| А1 | 2 | 4 | 3 | |
| А2 | 1 | 5 | 4 | |
| Потреби | 58 #50 |
Це відкрита транспортна задача, у якій 
.
Введемо фіктивний пункт відправлення А3 із запасом 8 (табл. 5.13)
Таблиця 5.13
| Пп Пв | В1 | В2 | В3 | Запаси |
| А1 | 2 | 4 | 3 | |
| А2 | 1 | 5 | 4 | |
| А3 | 0 | 0 | 0 | |
| Потреби | 58=58 |
Вийшла закрита транспортна задача. Вирішимо її методом
потенціалів (табл. 5.14, 5.15, 5.16, 5.17).
Таблиця 5.14 Таблиця 5.15
| Пп Пв | В1 | В2 | В3 | Запаси | αi | Пп Пв | В1 | В2 | В3 | Запаси | αi | |
| А1 |  2
| 4 | 3 3 | А1 | 2 2 |  4
| 5 3 | |||||
| А2 | 3 1 | 5 | 4 | А2 | 1 | 5 | 4 | |||||
| А3 | -1 0 | 1 0 | 0 | -3 | А3 | -3 0 | 1 0 | 0 | -4 | |||
| Потре би | 58=58 | Потре би | 58=58 | |||||||||
| βj | βj |
Таблиця 5.16 Таблиця 5.17
| Пп Пв | В1 | В2 | В3 | Запаси | αi | Пп Пв | В1 | В2 | В3 | Запаси | αi | |
| А1 |  0 2
| 4 | 3 | А1 | 0 2 | 4 | 3 18 | |||||
| А2 | 1 | 5 | 4 | А2 | 1 | 5 | 4 4 | |||||
| А3 | -3 0 | 1 0 | 0 | -3 | А3 | -4 0 | 0 | 0 | -4 | |||
| Потре би | 58=58 | Потре би | 58=58 | |||||||||
| βj | βj |
У таблиці 5.17 - оптимальний план перевезень для закритої транспортної задачі. Опускаємо перевезення з фіктивного пункту А3,
одержимо оптимальний план для відкритої транспортної задачі (табл.5.18).
fmin = 2• 4 + 18• 3 + 15• 1 + 15• 5 = 152
Потреба пункту В2 задоволена не повністю.
Таблиця 5.18
| Пн По | В1 | В2 | В3 | Запаси |
| А1 | 2 | 4 | 3 18 | |
| А2 | 1 | 5 | 4 | |
| Потре би |