 |
|
Після вибору генерального елемента переходимо до таблиці 3.11
Таблиця 3.11
| Б | 
| 
| 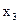
| z | Q |
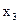
| -1 | ||||
| z | -2 | ||||
| g | -2 | -9 |
Звернемо увагу на стовпець 
 . Він показує, що цільова функція g не обмежена знизу на ОПР. Згадуючи, що g =-f, одержуємо відповідь.
. Він показує, що цільова функція g не обмежена знизу на ОПР. Згадуючи, що g =-f, одержуємо відповідь.
Відповідь: ЗЛП нерозв'язна через необмеженість зверху на ОПР цільової функції f.
Приклад 3. Вирішимо симплекс-методом задачу про використання обладнання, поставлену в параграфі 2.1. Саме там приводилася її математична модель
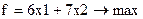

Приводимо ЗЛП до канонічного вигляду




Система рівнянь записана в жордановій формі з невід’ємними правими частинами, базисні змінні 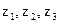 не входять у цільову функцію g. Тому табличний вигляд цільової функції такий:
не входять у цільову функцію g. Тому табличний вигляд цільової функції такий: 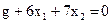 .
.
Заповнюємо симплекс-таблицю (таблиця 3.12).
Таблиця 3.12
| Б | 
| 
| 
| 
| 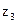
| Q |

| ||||||

| ||||||
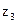
| ||||||
| G |
Умови оптимальності й нерозв'язності не виконуються. Стовпець  (у нижньому рядку якого стоїть найбільше додатне число) виберемо генеральним. Порівнюючи відносини 30:3, 40:2, і 60:4, обираємо перший рядок як генеральний. Поділивши його на 3 і зробивши за допомогою жорданової процедури нулі у всіх інших рядках генерального стовпця, після заміни базисної змінної
(у нижньому рядку якого стоїть найбільше додатне число) виберемо генеральним. Порівнюючи відносини 30:3, 40:2, і 60:4, обираємо перший рядок як генеральний. Поділивши його на 3 і зробивши за допомогою жорданової процедури нулі у всіх інших рядках генерального стовпця, після заміни базисної змінної  на змінну
на змінну  , одержимо таблицю 3.13.
, одержимо таблицю 3.13.
Таблиця 3.13
| Б | 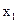
| 
| 
| 
| 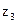
| Q |
| x2 | 
| 
| ||||
| z2 | 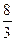
| 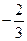
| ||||
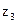
| 
| 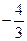
| ||||
| g | 
| 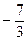
| -70 |
Знову вибираємо генеральний елемент і переходимо до таблиці 3.14
Таблиця 3.14
| Б | 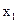
| 
| 
| 
| 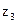
| Q |

| 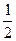
| 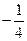
| ||||
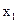
| 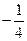
| 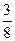
| 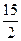
| |||
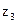
| 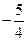
|  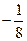
| 
| |||
| g | - 2 | 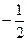
| -80 |
У нижньому рядку таблиці 3.14 стоять недодатні числа. Тому опорний план, що відповідає цій таблиці, оптимальний. Випишемо його:
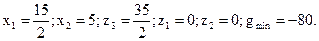
Оскільки змінні 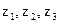 не фігурували у вихідній постановці задачі, крім того, функція f = - g у вихідній постановці максимізувалася, то можна записати наступне оптимальне рішення вихідної задачі
не фігурували у вихідній постановці задачі, крім того, функція f = - g у вихідній постановці максимізувалася, то можна записати наступне оптимальне рішення вихідної задачі

Повертаючись до змістовної постановки (параграф 2.1), доходимо наступного висновку: прибуток підприємства буде максимальним (80 грош.од.), якщо виробів А випустити 7,5 од., виробів В випустити 5 од.
Це ж завдання ми вирішили геометрично (див. параграф 2.5, приклад 5) і, природно, одержали саме такий результат.
3.7. Відшукування початкового опорного плану ЗЛП методом штучного базису
Щоб почати рішення ЗЛП симплекс-методом, потрібно привести її спочатку до канонічного вигляду, а потім - до табличного. Табличний вигляд вимагає, щоб система рівнянь канонічного вигляду була приведена до жорданової форми з невід’ємними правими частинами. Базисне рішення такої жорданової форми буде початковим опорним планом ЗЛП.
Приведення системи лінійних рівнянь до жорданової форми не являє собою труднощів, однак вимога невід’ємності правих частин ускладнює завдання. Крім того, якщо ОПР задачі порожня, то жорданової форми з невід’ємними правими частинами не існує (хоча жорданову форму система лінійних рівнянь може мати).
Систематична процедура, яка або виявляє нерозв'язність ЗЛП через порожнечу ОПР, або приводить систему лінійних рівнянь канонічного вигляду до жорданової форми з невід’ємними правими частинами (відшукує вихідний опорний план), називається методом штучного базису. Приступимо до викладу цього методу.
Нехай ЗЛП записана в канонічному вигляді.
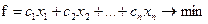 (3.5)
(3.5)
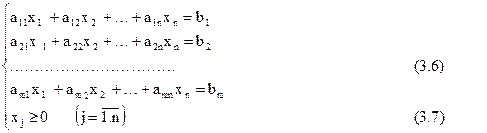
Насамперед потрібно зробити невід’ємними праві частини системи (3.6). Цього можна домогтися множенням на (-1) рівнянь із від’ємними правими частинами. Отже, будемо вважати, що
 (3.8)
(3.8)
Розглянемо допоміжну задачу, що записується в такий спосіб:
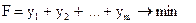 (3.9)
(3.9)

Змінні 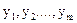 називаються штучними. Вони складають базис у жордановій формі (3.10), який називається штучним базисом.
називаються штучними. Вони складають базис у жордановій формі (3.10), який називається штучним базисом.
ОПР допоміжної задачі непорожня, тому що їй належить наступний набір значень змінних:  (див.(3.10),(3.11),(3.12)(3.8)). Цільова функція (3.9), що є сумою невід’ємних змінних, обмежена знизу на ОПР нулем:
(див.(3.10),(3.11),(3.12)(3.8)). Цільова функція (3.9), що є сумою невід’ємних змінних, обмежена знизу на ОПР нулем: 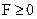 . Таким чином, для допоміжної задачі жодна із двох причин нерозв'язності не має місця, тому допоміжна задача розв'язна. Оскільки система рівнянь записана в жордановій формі з невід’ємними правими частинами, то ми можемо привести допоміжну задачу до табличного вигляду й вирішити симплекс-методом. Після вирішення можуть появитися два випадки.
. Таким чином, для допоміжної задачі жодна із двох причин нерозв'язності не має місця, тому допоміжна задача розв'язна. Оскільки система рівнянь записана в жордановій формі з невід’ємними правими частинами, то ми можемо привести допоміжну задачу до табличного вигляду й вирішити симплекс-методом. Після вирішення можуть появитися два випадки.
1.  (3.I3)
(3.I3)
Покажемо, що тоді вихідна задача (3.5 - 3.7) нерозв'язна через порожнечу ОПР. Дійсно, нехай, всупереч цьому твердженню, є припустиме рішення  вихідної задачі. Тоді набір значень змінних
вихідної задачі. Тоді набір значень змінних
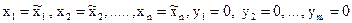
є, мабуть, припустимим рішенням допоміжної задачі. Значення цільової функції F при цьому припустимому рішенні дорівнює 0, що суперечить (3.13).
2.  (3.14)
(3.14)
Розглянемо останню симплекс-таблицю для допоміжної задачі. Випишемо відповідну цій таблиці жорданову форму з невід’ємними правими частинами. Тут можуть появитися дві можливості:
а) серед базисних змінних немає штучних. Тоді вилучаємо з жорданової форми всі члени, що містять штучні вільні змінні, одержимо жорданову форму з невід’ємними правими частинами для вихідної задачі;
б) серед базисних змінних є штучні. З огляду на (3.9) і (3.14), можна стверджувати, що в оптимальному плані значення всіх штучних змінних рівні 0. Тому права частина кожного рівняння, що містить штучну змінну за базисну, дорівнює 0, тобто таке рівняння можна записати так:
 (3.15)
(3.15)
Далі, якщо в рівнянні (3.15) коефіцієнти при всіх змінних  рівні 0 (інакше кажучи, воно фактично містить тільки штучні змінні), то вилучаємо таке рівняння з жорданової форми. Якщо ж рівняння вигляду (3.15) містить яку-небудь змінну
рівні 0 (інакше кажучи, воно фактично містить тільки штучні змінні), то вилучаємо таке рівняння з жорданової форми. Якщо ж рівняння вигляду (3.15) містить яку-небудь змінну  з ненульовим коефіцієнтом, то поділимо рівняння на коефіцієнт при
з ненульовим коефіцієнтом, то поділимо рівняння на коефіцієнт при  , одержимо рівняння вигляду:
, одержимо рівняння вигляду:
 (3.16)
(3.16)
За допомогою жорданової процедури вилучимо xj з інших рівнянь системи. Оскільки права частина рівняння (3.16) дорівнює 0, то праві частини інших рівнянь після вилучення xj не зміняться й залишаться невід’ємними .
За допомогою зазначених прийомів ми завжди можемо одержати жорданову форму з невід’ємними правими частинами, в якій серед базисних змінних немає штучних, і прийти, таким чином, до випадку а).
Приклад I. Вирішити симплекс-методом
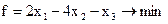
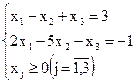
Задача записана в канонічному вигляді, однак права частина другого рівняння системи від’ємна. Тому систему рівнянь перепишемо так:

Запишемо допоміжну задачу


Вирішимо допоміжну задачу симплекс-методом. Для цього приведемо її до табличного вигляду
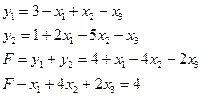
Табличний вигляд допоміжної задачі такий:

Побудуємо першу симплекс-таблицю (таблиця 3.15)
Таблиця 3.15
| Б | 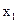
| 
| 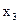
| 
| 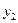
| Q |

| -1 | |||||
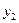
| -2 | |||||
| F | -1 |
Перейдемо до нової симплекс-таблиці (таблиця 3.16)
Таблиця 3.16
| Б | 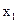
| 
| 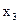
| 
| 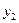
| Q |

| 
| 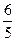
| 
| 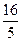
| ||

| 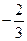
| 
| 
| 
| ||
| F | 
| 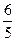
| 
| 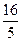
|
Переходимо до наступної симплекс-таблиці. Звернемо увагу на те, що за генеральний стовпець був узятий перший, а не третій стовпець - це наше право!
Таблиця 3.17
| Б | 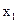
| 
| 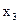
| 
| 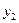
| Q |
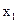
| 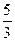
| 
| 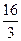
| |||

| 
| 
| 
| |||
| F | -1 | -1 |
Ми досягли оптимального плану для допоміжної задачі; при цьому  . Випишемо жорданову форму, що відповідає таблиці 3.17:
. Випишемо жорданову форму, що відповідає таблиці 3.17:

Опустивши штучні змінні, одержимо жорданову форму з невід’ємними правими частинами для вихідної задачі:

Тепер приступаємо до вирішення вихідної задачі. Приведемо її до табличного вигляду
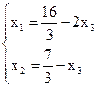
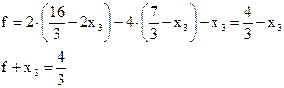
Складемо симплекс-таблицю для вихідної задачі (таблиця 3.18) і переходимо до наступної таблиці 3.1
Таблиця 3.18
| Б | 
| 
| 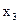
| Q |

| 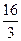
| |||

| 
| |||
| F | 
|
Таблиця 3.19
| Б | 
| 
| 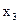
| Q |

| -2 | 
| ||
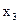
| 
| |||
| F | -1 | -1 |
Одержимо оптимальне рішення:

З метою часткового контролю правильності обчислень можна переконатися у тому, що отримане рішення є припустимим рішенням вихідної задачі, значення цільової функції при якому дорівнює -1.
Приклад 2. Вирішити симплекс-методом
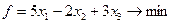

Складемо допоміжну задачу

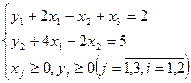
Відомими прийомами приведемо її до табличного виду:

Заповнимо симплекс-таблицю (таблиця 3.20)
Таблиця 3.20
| Б | 
| 
| 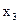
| 
| 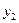
| Q |

| -1 | |||||
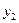
| -2 | |||||
| F | -3 |
Перейдемо до нової симплекс-таблиці (3.21)
Таблиця 3.21
| Б | 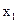
| 
| 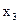
| 
| 
| Q |
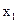
| 
| 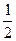
| 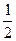
| |||

| -2 | -2 | ||||
| F | -2 | -3 |
Одержимо оптимальний план. Значення цільової функції при оптимальному плані  . Тому вихідна ЗЛП нерозв'язна через порожнечу ОПР.
. Тому вихідна ЗЛП нерозв'язна через порожнечу ОПР.
Цікаво відзначити, що система лінійних рівнянь вихідної ЗЛП сумісна й приводиться до жорданової форми. Однак вона не приводиться до жорданової форми з невід’ємними правими частинами.
Зробимо ще одне корисне зауваження. У розглянутому прикладі 2 можна було б скласти більш просту допоміжну задачу:

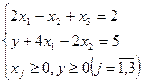
Справа в тому, що мета введення штучних змінних - одержання жорданової форми з невід’ємними правими частинами для допоміжної задачі. Тут ця мета досягається за допомогою однієї штучної змінної у . Припустимий базис складається зі змінних 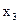 і у .
і у .
3.8. Виродженість опорного плану. Зациклення
Опорний план ЗЛП називається виродженим, якщо деякі з базисних змінних приймають значення 0. У цьому випадку при переході від одного плану до іншого може не відбутися зменшення цільової функції.
Приклад. Нехай табличний вигляд ЗЛП такий:

Складемо першу симплекс-таблицю (таблиця 3.22).
Таблиця 3.22
| Б | 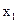
| 
| 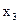
| 
| Q |
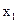
| -1 | ||||

| |||||
| f |
Опорний план, що відповідає цій симплекс-таблиці, є виродженим, тому що значення базисної змінної 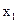 дорівнює 0. Перейдемо до нової симплекс-таблиці (табл.3.23)
дорівнює 0. Перейдемо до нової симплекс-таблиці (табл.3.23)
Таблиця 3.23
| Б | 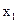
| 
| 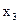
| 
| Q |
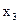
| -1 | ||||

| -2 | ||||
| f | -2 |
При новому опорному плані значення цільової функції залишилося колишнім: f=4.
При вироджених опорних планах можлива ситуація, коли, послідовно переходячи від одного опорного плану до іншого, через певну кількість кроків можна повернутися до колишнього опорного плану, так і не досягши мінімуму функції. Це називається зацикленням.
На практиці зациклення зустрічається вкрай рідко. Існує така модифікація симплекс-алгоритму, при якій зациклення виключається. Для практичних цілей достатня й наступна рекомендація: якщо відбулося зациклення, то з першою ж нагодою потрібно інакше вибрати генеральний елемент, ніж це робилося в перший раз.
Справедлива теорема про кінцевість симплекс-алгоритму: якщо ЗЛП розв'язна, то оптимальне рішення завжди може бути знайдене за допомогою симплекс-методу, причому починати можна з будь-якого опорного плану.