 |
|
Параметрическое и каноническое уравнения прямой
МЕТОДЫ АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ НА ПЛОСКОСТИ
3.1. Декартовы координаты. Векторные пространства R1 и R2 на координатной плоскости.
Рис. 3.1. Векторные пространства R1 и R2 на координатной плоскости.
Обозначим одномерные векторные пространства 
, 
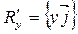. Они соответствуют координатным осям Ох и Оy.
Множество векторов расположенных или параллельных некоторой прямой (s), образует одномерное векторное пространство, которое обозначается 
. Вектор 
называется направляющим вектором прямой (s), а пространство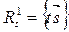 
называется направляющим пространством прямой (s).
Пусть М – любая точка плоскости. Обозначим проекции вектора 
на оси Ох и Оy через х и y, тогда 
. Упорядоченную пару чисел (х, y) будем называть координатами вектора и обозначать 
. Множество векторов 
образует векторное пространство R2. Множество точек 
образует точечное (афинное) двумерное пространство.
Каждой паре точек A(x1; y1) и В(x2; y2) соответствует вектор 
. Числа 
называются координатами вектора 
.
Параметрическое и каноническое уравнения прямой
Пусть прямая проходит через данную точку M0(x0; y0) параллельно данному вектору 
(рис. 3.2). Вектор 
называется направляющим вектором прямой. Подпространство { 
} называется направляющим подпростанством прямой 
. Приложим вектор и подпространство { } к точке M0. Тогда каждой точке М на прямой соответствует некоторое число t такое что, 
.
Отсюда получаем, 
, 
. (3.1)
Рис. 3.2. Прямая и направляющее подпространство на координатной плоскости
Таким образом, множество векторов 
прямой получается из множества { } сдвигом на вектор 
, или, иначе, прямая получается сдвигом направляющей прямой (полупространства { }) на вектор . Из векторного уравнения (3.1) получаем систему уравнений для координат точки M(x; y):
. (3.2)
Систему (3.2) называют параметрическими уравнениями прямой. Исключая параметр t из системы (3.2) получаем уравнение:
, (3.3)
которое называется каноническим уравнением прямой.
Пример 3.1. Написать уравнение прямой, проходящей через точку М0(2,-3) параллельно вектору 
=(-4,3) в параметрической и канонической формах.
Решение. Пусть М(х,y) – текущая точка прямой, t - ее параметр, тогда из (3.1) получаем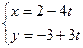 
- параметрическое уравнение прямой, а из (3.2) получаем 
- каноническое уравнение прямой.
Любое линейное алгебраическое уравнение с двумя переменными x, y 
определяет единственным образом прямую на координатной плоскости Оxy.
Действительно, пусть а ≠ 0, тогда 
, 
, 
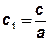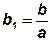. Обозначим y = t.
Получаем параметрическое уравнение прямой:
, проходящей через точку М0 (-с1, 0) и направляющим вектором 
.
Уравнение называют общим уравнением прямой на плоскости.