 |
|
Объяснение закона Хаббла
Допустим, есть источник, расположенный в сопутствующей системе на расстоянии r1 от наблюдателя. Приёмная аппаратура наблюдателя регистрирует фазу приходящей волны. Рассмотрим два интервала между точками с одной и тойже фазой:
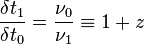
С другой стороны для световой волны в принятой метрике выполняется равенство:

Если это уравнение проинтегрировать и вспомнить, что в сопутствующих координатах r не зависит от времени, то при условии малости длины волны относительно радиуса кривизны Вселенной получим соотношение:

Если теперь его подставить в первоначальное соотношение:

После разложения правой части в ряд Тейлора с учётом члена первого порядка малости получим соотношение в точности совпадающее с законом Хаббла. Где постоянная H принимает вид:
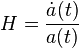
ΛCDM
| Космологические параметры по данным WMAP и Planck | ||
| WMAP | Planck | |
| Возраст Вселенной t0 млрд лет | 13,75±0,13 | 13,81±0,06 |
| H0 км/с/МПк | 71,0±2,5 | 67,4±1,4 |
| Плотность барионной материи Ωbh2 | 0,0226±0,0006 | 0,0221±0,0003 |
| Плотность тёмной материи Ωсh2 | 0,111±0,006 | 0,120±0,003 |
| Общая плотность Ωt | 1,08+0,09-0,07 | 1,0±0,02 |
| Плотность барионной материи Ωb | 0,045±0,003 | |
| Плотность тёмной энергии ΩΛ | 0,73±0,03 | 0,69±0,02 |
| Плотность тёмной материи Ωc | 0,22±0,03 |
Как уже говорилось, уравнения Фридмана допускают множество решений, в зависимости от параметров. И современная модель ΛCDM — это модель Фридмана с общепринятыми параметрами. Обычно в работе наблюдателей они приводятся в понятиях, связанных с критической плотностью:

Если выразить левую часть из закона Хаббла, то после приведения получим следующий вид:
 ,
,
где Ωm=ρ/ρcr, Ωk = -(kc2)/(a2H2), ΩΛ=(8πGΛc2)/ρcr. Из этой записи видно, что еслиΩm+ΩΛ= 1 , т. е. суммарная плотность материи и тёмной энергии равна критической, то k = 0, т. е. пространство плоское, если больше, то k = 1, если меньше k= -1
В современной общепринятой модели расширения космологическая постоянная положительна и существенно отлична от нуля, то есть на больших масштабах возникают силы антигравитации. Природа таких сил неизвестна, теоретически подобный эффект можно было бы объяснить действием физического вакуума, однако ожидаемая плотность энергии оказывается на много порядков больше, чем энергия, соответствующая наблюдаемому значению космологической постоянной — проблема космологической постоянной.
Остальные варианты на данный момент представляют только теоретический интерес, однако это может измениться при появлении новых экспериментальных данных. Современная история космологии уже знает подобные примеры: модели с нулевой космологической постоянной безоговорочно доминировали (помимо короткого всплеска интереса к другим моделям в 1960-е гг.) с момента открытия Хабблом космологического красного смещения и до 1998 года, когда данные по сверхновым типа Ia убедительно опровергли их.