 |
|
Алгебраическая форма комплексного числа
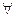 z=(a,b)
z=(a,b)  ℂ: z=(a,b)=(a,0)+(0,b)=(a,0)+(b,0)(0,1)
ℂ: z=(a,b)=(a,0)+(0,b)=(a,0)+(b,0)(0,1)  a+bi, где a,b
a+bi, где a,b  ℝ.
ℝ.
Определение 4. Представление комплексного числа z=(a,b) в виде z=a+bi, где a,b  ℝ, i2=-1, называется алгебраической формой комплексного числа z; а называется действительной частью комплексного числа z, b – мнимая частью комплексного числа z, элемент i называется мнимой единицей.
ℝ, i2=-1, называется алгебраической формой комплексного числа z; а называется действительной частью комплексного числа z, b – мнимая частью комплексного числа z, элемент i называется мнимой единицей.
Операции над комплексными числами в алгебраической форме
Пусть z1=a+bi, z2=c+di.
1. Сложение: z1+z2=(a+c)+(b+d)i.
2. Умножение: z1  z2=(ac-bd)+(ad+bc)i.
z2=(ac-bd)+(ad+bc)i.
Определение 5. Пусть z=a+bi  ℂ. Комплексное число
ℂ. Комплексное число  =a-bi называется комплексно сопряженным с числом z.
=a-bi называется комплексно сопряженным с числом z.
3. Деление:
z1:z2=(z1  2): (z2
2): (z2  2)=
2)= 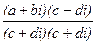 =
= 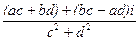 =
=  .
.
4. Извлечение квадратного корня:
Пусть z=a+bi. Найдем  :
:
пусть  =x+yi
=x+yi  z=(x+yi)2, т.е. a+bi=(x2+y2)+2xyi
z=(x+yi)2, т.е. a+bi=(x2+y2)+2xyi 
 .
.
Таким образом, нахождение  сводится к решению системы уравнений
сводится к решению системы уравнений  .
.
31.  Тригонометрическая форма комплексного числа
Тригонометрическая форма комплексного числа
Каждому комплексному числу z=(а;b) соответствует на плоскости в декартовой системе координат точка с координатами (а;b). Верно и обратное. Каждой точке на плоскости в декартовой системе координат соответствует упорядоченная пара действительных чисел, то есть соответствует некоторое комплексное число. Таким образом, между множеством ℂ и множеством всех точек плоскости существует взаимно однозначное соответствие. Это означает, что мы можем считать, что каждое комплексное число изображается точкой на плоскости. Поэтому, плоскость также называют комплексной плоскостью.
Пусть z=(а;b)=а+bi. Изобразим число z на плоскости:

 b .М (а;b)
b .М (а;b)
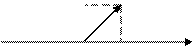
0 а
Любая точка на плоскости может определяться не только своими декартовыми координатами, но и координатами, которые называются полярными: М(r; 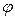 ), где r=|ОМ|,
), где r=|ОМ|,  – угол между Ox и ОМ.
– угол между Ox и ОМ.
Таким образом, каждое комплексное число должно однозначно определяться своими полярными координатами r и  .
.
Определение 6. Модулем комплексного числа z=а+ib называется длина радиус-вектора ОМ точки М (а;b), и обозначается |z|=r.
Из  ОАМ
ОАМ  r =
r =  a2+b2 (1).
a2+b2 (1).
Определение 7. Аргументом комплексного числа z=a+bi называется угол 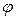 между положительным направлением оси Ox и радиус-вектором ОМ точки М (а;b), и обозначается arg z=
между положительным направлением оси Ox и радиус-вектором ОМ точки М (а;b), и обозначается arg z= 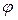 .
.
Аргумент комплексного числа определяется не однозначно, а с точностью до 2  . Значение аргумента, принадлежащее интервалу [0; 2
. Значение аргумента, принадлежащее интервалу [0; 2  ] называется главным значением аргумента, и обозначается Arg z.
] называется главным значением аргумента, и обозначается Arg z.
аrg z=Arg z+2  k , k
k , k  ℤ.
ℤ.
 Из
Из  ОАМ
ОАМ  сos
сos  =a/r
=a/r
sin  =b/r (2).
=b/r (2).
Таким образом, z =a+ib = r  cos
cos  + r
+ r  sin
sin 
 i = r
i = r  (cos
(cos  +i
+i  sin
sin  ).
).
Запись z=r  (cos
(cos  +i
+i  sin
sin  ) (3) называется тригонометрической формой комплексного числа z.
) (3) называется тригонометрической формой комплексного числа z.
Замечание. Для комплексного числа 0 модуль равен нулю, а аргумент не определяется. Поэтому тригонометрической формой числа 0 является следующая запись: 0= 0  (cos
(cos  +i
+i  sin
sin  ), где
), где  - произвольный угол.
- произвольный угол.
Операции над комплексными числами в тригонометрической форме
Пусть z1 = r1 (cos  1+isin
1+isin  1), z2 = r2 (cos
1), z2 = r2 (cos  2+ isin
2+ isin  2).
2).
1) Умножение комплексных чисел:
z1  z2 =r1
z2 =r1  r2 ((cos
r2 ((cos  1
1  cos
cos  2 –sin
2 –sin  1
1  sin
sin  2 ) + ( sin
2 ) + ( sin  1
1  cos
cos  2 + sin
2 + sin  2
2  cos
cos  1 )) = r1
1 )) = r1  r2 (cos (
r2 (cos (  1 +
1 +  2 )+i sin (
2 )+i sin (  1 +
1 +  2 )).
2 )).
Таким образом, z1  z2 = r1
z2 = r1  r2 (cos (
r2 (cos (  1 +
1 +  2 ) + i sin (
2 ) + i sin (  1 +
1 +  2 )) (4).
2 )) (4).
2) Деление комплексных чисел: пусть z2 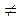 0. Тогда
0. Тогда
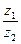 =
= 
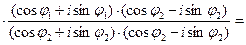

= 
=  (cos (
(cos (  1 -
1 -  2 )+i sin (
2 )+i sin (  1-
1-  2 )).
2 )).
Таким образом,  =
=  (cos (
(cos (  1 -
1 -  2 )+i sin (
2 )+i sin (  1-
1-  2 )) (5) .
2 )) (5) .
3) Возведение в степень:
Пусть z = r (cos  +i sin
+i sin  )
) 
z2 = z  z= r2 (cos2
z= r2 (cos2  +i sin2
+i sin2  ) и т.д.
) и т.д.
Методом математической индукции можно доказать, что
zn = rn (cos(n  )+i sin(n
)+i sin(n  )), n
)), n  ℕ (6).
ℕ (6).
Формула (6) называется формулой Муавра.
Определение 8. Корнем n-й степени из комплексного числа z называется такое комплексное число z0, что z0n = z ,  = z0.
= z0.
4) Извлечение корня n-й степени из комплексного числа z: пусть z  .
.
Найдём z0. Пусть z0=r0 (cos  0+isin
0+isin  0)
0) 
 (r0 (cos
(r0 (cos  0+isin
0+isin  0)) n = r (cos
0)) n = r (cos  +isin
+isin  )
)  r0n=r
r0n=r
 r0n (сos (n
r0n (сos (n  0 ) + isin (n
0 ) + isin (n  0 ))= r (cos
0 ))= r (cos  +isin
+isin  )
)  n
n  0 =
0 =  +2
+2  k , k
k , k  ℤ
ℤ 
 r0 =
r0 = 

 0 =
0 =  , k
, k  ℤ.
ℤ.
Пусть k=0:  01 =
01 = 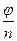 ;
;
Пусть k=1:  02 =
02 =  ;
;
Пусть k=2:  03 =
03 = 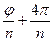 ;
;
Пусть k=n-1:  04 =
04 = 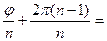
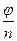 +2
+2  -
- 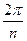 ;
;
Пусть k=n:  05 =
05 = 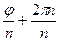 =
= 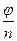 +2
+2  =
=  0 1;
0 1;
Пусть k=n+1:  06 =
06 = 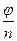 +2
+2  +
+ 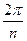 =
=  02 и т. д.
02 и т. д.
Таким образом,  =
=  (cos
(cos 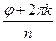 +i sin
+i sin 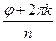 ), k=
), k=  (7) .
(7) .
Корень n-й степени из комплексного числа z имеет n значений z0,z1,z2,…,zn , которые на комплексной плоскости располагаются на окружности радиуса 
и делят окружность на n равных частей.
32. Корни n-й степени из единицы
Теорема 1. Корни n-й степени из единицы образуют мультипликативную абелеву группу порядка n.
Теорема 2. Если одно из значений корня n-ной степени из комплексного числа 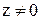 умножить на каждое из значений корня n-ной степени из 1, то получим все значения корня n-ной степени из z.
умножить на каждое из значений корня n-ной степени из 1, то получим все значения корня n-ной степени из z.
Доказательство. Пусть 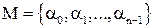 - множество всех значений корня n-ной степени из z,
- множество всех значений корня n-ной степени из z, 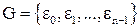 - множество всех значений корня n-ной степени из 1. Пусть
- множество всех значений корня n-ной степени из 1. Пусть  , где
, где  и
и 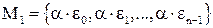 . Покажем, что
. Покажем, что 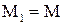 .
.
1) Покажем, что  . Пусть
. Пусть 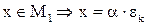 , где
, где 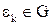 . Покажем, что
. Покажем, что 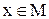 . Достаточно показать, что
. Достаточно показать, что  . Действительно,
. Действительно,
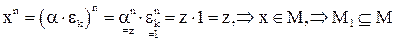 .
.
2) Покажем, что 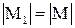 . По заданию
. По заданию  ,
,  не больше n, т.е.
не больше n, т.е.  . Таким образом,
. Таким образом,  . Допустим, что
. Допустим, что 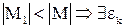 и
и 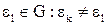 , но
, но 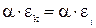 . Рассмотрим
. Рассмотрим 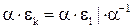 слева,
слева, 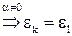 . Противоречие,
. Противоречие, 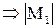 не меньше
не меньше 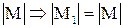 .
.
Из 1) и 2)  . Теорема доказана.
. Теорема доказана.
Первообразные корни
Пустъ εk – корень m-ой степени из 1.
Пусть 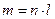 , где n,m,l
, где n,m,l  N. Тогда
N. Тогда 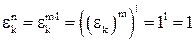 m)l=1l=1, Þ ek – корень n-ой степени из 1.
m)l=1l=1, Þ ek – корень n-ой степени из 1.
Таким образом, корень n-ной степени из 1 может оказаться корнем из 1 и другой степени, меньшей n.
Например, найдём 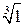 и
и 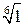 .
.
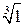
| 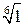
|
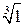 =cos =cos 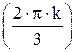 +i×sin +i×sin 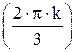 , k= , k=  e0¢=cos(0)+i×sin(0)
e1¢=cos
e0¢=cos(0)+i×sin(0)
e1¢=cos  +i×sin +i×sin  e2¢=cos
e2¢=cos  +i×sin +i×sin 

|  =cos =cos 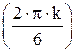 +i×sin +i×sin 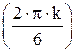 , k= , k=  e0=cos(0)+i×sin(0)
e1=cos
e0=cos(0)+i×sin(0)
e1=cos 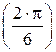 +i×sin +i×sin 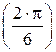 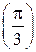 e2=cos
e2=cos  +i×sin +i×sin   e3=cos
e3=cos 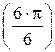 +i×sin +i×sin 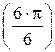 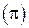 e4=cos
e4=cos  +i×sin +i×sin   e5=cos
e5=cos  +i×sin +i×sin  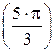
|
Корни ε0, e2 и e4 шестой степени из 1 являются также корнями третьей степени из 1.
Определение 1. Корень ek n-ой степени из 1 называется первообразным корнем n-ой степени из 1, если ek не является корнем из 1 никакой степени меньшей чем n.
Из примера следует, что e0, e2, e4 не являются первообразными корнями шестой степени из 1.
Теорема 3. Корень e1 n-ой степени из 1 является первообразным, где n  N.
N.
Доказательство. Допустим, что ε1 не является первообразным корнем из 1 n-ой степени, тогда $ m  N и m<n, такое что ε1 - корень m-ой степени из 1.
N и m<n, такое что ε1 - корень m-ой степени из 1.
Рассмотрим ε1 : 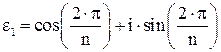 .
.
Так как  , то
, то  ,
, 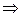
 , k
, k 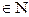 ,
,  , Þ
, Þ  . Противоречие с тем, что m<n, Þ ε1 - первообразный корень n-ной степени из 1. Теорема доказана.
. Противоречие с тем, что m<n, Þ ε1 - первообразный корень n-ной степени из 1. Теорема доказана.
Теорема 4. Корень εk n-ой степени из 1 является первообразным корнем n-ой степени из 1 Û k и n имеют наибольший общий делитель равный 1, то есть 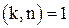 .
.
Из теоремы Þ ε3 : 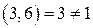
ε5: 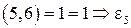 - первообразный корень шестой степени из 1.
- первообразный корень шестой степени из 1.
Таким образом, 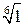 имеет 2 первообразных корня: ε1 и ε5.
имеет 2 первообразных корня: ε1 и ε5.
Теорема 5. Если первообразный корень εk n-ной степени из 1 возвести в 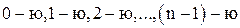 степени, то получим все корни n-ной степени из 1.
степени, то получим все корни n-ной степени из 1.