Главная | Обратная связь

Свойства сходящихся рядов

Теорема 19 (о сочетательности ряда). Сходящийся ряд обладает сочетательным свойством: при произвольной группировке его членов с сохранением их порядка получается сходящийся ряд с прежней суммой. Причем, если была абсолютная сходимость, то она тоже сохранится.

Доказательство. Пусть ряд (1) сходится к 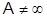, т.е. 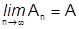, где - частичная сумма ряда (1).

Образуем произвольные группы членов, оставляя их на своих местах:

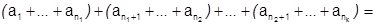
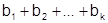(2)

Обозначим 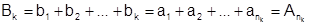. По условию , тогда 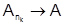и, следовательно, , т.е. ряд (2) сходится к сумме A.

Пусть ряд (1) абсолютно сходится, т.е. сходится вместе с рядом

. (3)

Тогда по признаку сходимости положительных рядов (смотри теорему 6) последовательность частичных сумм , где

,

ограничена сверху: .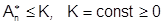

Для ряда

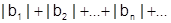(4)

имеем

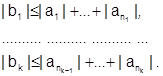
Тогда для ряда (4) верно

,

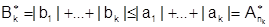т.е. . Ограниченность последовательности 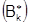сверху по названному выше признаку означает сходимость положительного ряда (4), а это, в свою очередь, означает, что ряд (2) абсолютно сходится. ¨

Замечание. Сочетательность в обратном порядке в общем случае не имеет место. Переход от (2) к (1), т.е. раскрытие скобок может не сохранить сходимость.

Например, рассмотрим ряд 0+0+…+0+…, сходящийся к нулю. Его можно записать в виде (1-1)+(1-1)+…+(1-1)+… . Если в этом ряде раскрыть скобки, то получим ряд 1-1+1-1+…+(-1)^n-1+… , который расходится, т.к. .

Теорема 20 (о перестановке положительного ряда). Любая перестановка членов сходящегося положительного ряда сохраняет сходимость и сумму ряда.

Доказательство. Пусть положительный ряд (1) сходится к сумме 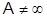. Тогда возрастая, т.е. .

После произвольной перестановки его членов получим ряд

, (5)

каждый член которого под каким-либо номером стоит в ряде (1). Возьмем 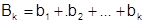. Один из членов в ряде (1) стоит самым правым, пусть он стоит там под номером m. Тогда в сумме участвуют все , поэтому

,

т.е. . Это означает, что последовательность ограничена сверху, а потому ряд (5) сходится к некоторой конечной сумме В, при этом

.

Таким образом, после перестановки получается сходящийся ряд, сумма которого не превосходит исходной.

Но ряд (1) тоже получается перестановкой из ряда (5), поэтому сумма А ряда (1), в свою очередь, не превосходит сумму В ряда (5) .

Итак, мы имеем с одной стороны , а с другой стороны - . Следовательно, А=В. Т.е. сумма ряда после перестановки сохраняется. ¨

Теорема 21 (теорема Дирихле - о перестановке абсолютно сходящегося ряда). Любая перестановка абсолютно сходящегося ряда сохраняет его сумму и абсолютную сходимость.

Доказательство: Пусть ряд (1) абсолютно сходится, т.е. сходится вместе с рядом (6)

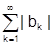После перестановки получаем ряды (7), (8)

По теореме 20 перестановка положительного сходящегося ряда (6) сохраняет его сходимость, значит, сходится ряд (8), а это означает абсолютную сходимость ряда (7), полученного перестановкой данного ряда (1).

По теореме Коши (теорема 16) сумма S абсолютно сходящегося ряда (1) равна: S=P-Q, где P и Q - суммы положительных рядов 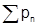и 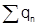, составленных соответственно из неотрицательных членов 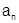и из модулей отрицательных членов 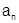ряда (1).

Перестановка ряда (1) переставляет и ряды 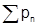и 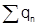, но по теореме 20 их суммы P и Q сохраняются, а значит сохраняется и сумма S=P-Q. ¨

Оказывается, что переместительным свойством обладают только абсолютно сходящиеся ряды.

Теорема Римана. Члены неабсолютно сходящегося ряда всегда можно так переставить, что получится новый ряд с любой заранее заданной суммой S и даже расходящийся.

Теорема Римана подчеркивает, что неабсолютная сходимость имеет место исключительно благодаря удачному расположению членов ряда, при котором отрицательные и положительные члены взаимно погашаются, и именно поэтому существенно зависит от порядка, в котором они следуют один за другим. Абсолютная же сходимость от порядков членов не зависит, следовательно, она возможна только благодаря достаточно быстрому стремлению членов к нулю.

Умножение рядов

Теорема 22 (об умножении рядов). Если ряды

(1)

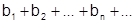(2)

абсолютно сходятся к суммам А и В, то ряд, составленный из всевозможных произведений их членов, взятых в произвольном порядке:

, (3)

тоже абсолютно сходится и имеет сумму .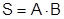

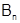Доказательство: По условию, если и - частичные суммы рядов (1) и (2), то 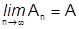и 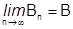, А и В - конечные.

Кроме того, сходятся к некоторым конечным суммам и , ряды

, (4)

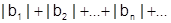, (5)

причем, последовательности частичных сумм и этих положительных рядов стремятся к своим пределам возрастая: .

Нужно доказать, что сходится ряд , (6)

что будет означать абсолютную сходимость ряда (3) и что сумма ряда (3) .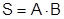

Пусть 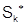- частичные суммы ряда (6):

,

т.к. справа после раскрытия скобок есть лишние члены.

Пусть 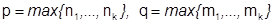, тогда все члены первой скобки участвуют в сумме , поэтому .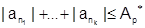

Аналогично 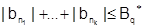, значит,

.

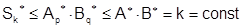Таким образом, у положительного ряда (6) последовательность частичных сумм ограничена сверху, следовательно, он сходится и этим доказана абсолютная сходимость ряда (3).

Для нахождения суммы S воспользуемся тем, что, что в силу абсолютной сходимости ряда (3) любая перестановка его членов сохраняет сумму и по теореме 19 эта сумма сохраняется при произвольной группировке его членов.

Расположим и сгруппируем члены наиболее удобным образом согласно таблице:

			...
			...
			...
...	...	...

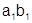
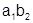
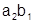
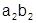
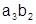
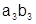
Получим ряд, имеющий ту же сумму S:

.

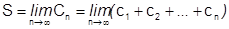Но 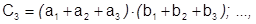т.е. . Поэтому

. ¨

Если составить ряд, группируя произведения по диагонали таблицы:

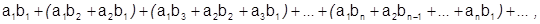
то его называют произведением рядов по Коши. Он получен перестановкой и группировкой абсолютно сходящегося ряда (3), поэтому его сумма такая же, и ряд тоже сходится абсолютно.

Можно доказать, что произведение рядов по Коши сходится (может быть не абсолютно) даже тогда, когда из двух сходящихся рядов (1) и (2) только один сходится.

Пример:

Ряды абсолютно сходятся (можно проверить признаком Даламбера). К некоторым суммам А и В. Найдем .

По теореме = сумме произведения рядов при людом способе умножения. Пользуясь этим выберем способ умножения по Коши.

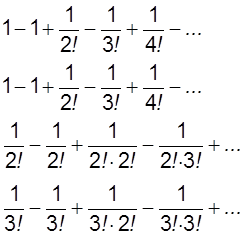
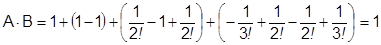
Ответ:

Вопросы для самоконтроля по главе 1.

1. Что называется частичной суммой числового ряда?

2. Какая существует связь между 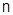и -й частичными суммами ряда?

3. Что называется суммой ряда?

4. Какой ряд называется сходящимся?

5. Какой ряд называется расходящимся?

6. Какое из двух нижеприведенных утверждений истинно, а какое ложно?
а) Если общий член ряда стремится к нулю при , то ряд сходится.
б) Если ряд сходится, то .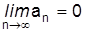

7. Как вычисляется сумма остатка сходящегося ряда, если известны сумма ряда и частичная сумма ?

8. Может ли расходится последовательность сумм остатков сходящегося ряда? К какому пределу она стремится?

9. Как определяется сумма и разность рядов? Какие утверждения можно сформулировать для суммы и разности двух рядов?

10. Как определяется произведение ряда на число? Как использовать операцию умножения ряда на число для записи разности двух рядов?

11. Как определить линейную комбинацию двух рядов 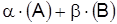, где , а .

12. Что может произойти с рядом, если произвести группировку членов путем расстановки скобок?

13. Может ли сходиться произведение расходящегося ряда на число?

14. Чем отличается функциональный ряд от числового ряда?

15. Пусть 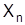- область определения 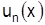, на каком множестве имеет смысл ряд ?

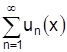16. Какой из методов интегрирования используется для вывода формулы Тейлора?

17. Как разложить многочлен n-й степени по степеням ?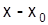

18. Пусть на промежутке 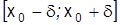функция f(x) имеет непрерывные производные до 10-го порядка включительно. С каким максимальным числом членов заведомо можно записать формулу Тейлора с остаточным членом в интегральной форме?

19. При каком условии можно записать ряд Тейлора функции f(x) по степеням ?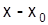

20. При каком условии справедливо равенство ?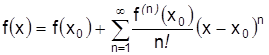

21. Всегда ли ряд Тейлора для функции f сходится к этой функции?

22. Что общего в разложении в степенной ряд функци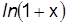й и ?

23. Что объединяет приемы разложения в степенной ряд функций и ?

24. Укажите множества аргументов, для которых имеют место стандартные разложения функций .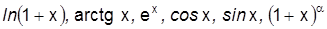

25. Если последовательность частичных сумм ряда с неотрицательными членами ограничена сверху, то можно ли утверждать, что ряд сходится? Почему?

26. Сформулируйте необходимое и достаточное условие сходимости ряда с неотрицательными членами.

27. Сформулируйте признаки сравнения положительных рядов.

28. Если для частичных сумм и 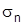двух рядов (А): и (В): с неотрицательными членами для каждого номера n имеет место соотношение , то и для суммы этих рядов и также справедливо соотношение . Почему это так? Какой смысл можно придать соотношению , если ряд (А) расходится или если ряд (В) расходится?

29. Члены числового ряда (А): , начиная с тысячного, положительны и при 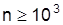выполняется неравенство . Что можно сказать о сходимости ряда (А)? Можно ли указать какое-либо соотношение между суммой ряда (А) и суммой ряда , равной 1?

30. На сравнении с каким рядом основывается доказательство признаков Даламбера и Коши сходимости рядов с положительными членами? Сформулируйте эти признаки.

31. На основании какого признака исследуется сходимость ряда ? Как называют этот ряд при ?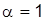

32. Для каких рядов можно применить интегральный признак Коши?

33. Изменится ли сумма сходящегося ряда, если в нем поменять местами конечное число членов ряда?

34. Дан сходящийся положительный ряд , каждый член которого представляет сумму конечного числа слагаемых: 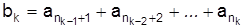. В каком случае в этом ряду можно опустить скобки?

35. Какой ряд называется знакочередующимся рядом?

36. К каким знакочередующимся рядам применима теорема Лейбница о знакочередующихся рядах?

37. На какую теорему из "Введения в анализ" опирается доказательство теоремы Лейбница?

38. Общий член знакочередующегося ряда не стремится к нулю. Что можно сказать об этом ряде?

39. При приближенном вычислении суммы знакочередующегося ряда, члены которого по абсолютной величине, монотонно убывая, стремятся к нулю, взято 11 первых членов ряда. Как оценить допущенную при этом погрешность?

40. Если в абсолютно сходящемся ряде у произвольного числа членов изменить знаки на противоположные, то нарушится ли при этом абсолютная сходимость ряда? Почему?

41. В сходящемся знакопостоянном ряде у бесконечного множества членов изменили знаки на противоположные. Будет ли сходиться полученный таким образом ряд? Если да, то как (абсолютно, условно)?

42.Ряд сходится условно. Изменится ли его сумма, если в нем поменять местами конечное число членов?

43.Некоторый ряд остается сходящимся при любой перестановке его членов. Что можно сказать о характере сходимости?

44.Можно ли из условно сходящегося ряда путем перестановки его членов получить расходящийся ряд?