Главная | Обратная связь

Импульсная характеристика. Свертка.

Изучим, каким образом линейная система может преобразовывать

входной сигнал в выходной. Для этого рассмотрим реакцию системы на

цифровую дельта-функцию (другое название - функция Кронекера).

Дельта-функция (цифровая) – это сигнал вида δ(x)= 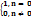, то есть короткий единичный импульс. Любой дискретный сигнал можно разложить в сумму таких функций, сдвинутых во времени. Например, бесконечный сигнал x[n] можно представить в виде . Здесь дельта-функции – это «базисные функции», а x[i] – это их коэффициенты в линейной комбинации.

Исследуем отклик линейной системы на цифровую дельта-функцию. Для этого подадим дельта-функцию в систему и измерим выходной сигнал. Пусть δ [n] →h[n]. Зная h[n] (отклик системы на дельта-функцию), можно вычислить отклик системы на любой входной сигнал. Так как любой входной сигнал является линейной комбинацией сдвинутых во времени дельта-функций, то выходной сигнал будет той же самой линейной комбинацией сдвинутых во времени функций h[n]. Это следует из линейности системы и инвариантности к сдвигу во времени.

Результирующая формула для вычисления выходного сигнала y[n] по

входному сигналу x[n]: .h[n] - импульсная характеристика системы.

Нахождение h(n) на примере. Дискретное изображение – это двумерный сигнал x[i,j], обозначающий яркость изображения в каждой дискретной точке (i,j) на плоскости. Дельта-функция в двумерном случае – это единичная светлая точка с координатами (0,0) на черном фоне. Пусть наша линейная система такова, что она отвечает на дельта-функцию функцией h[i,j], такой что h[i,j]=const на всех точках внутри круга с центром в точке (0,0) и диаметром 3 и равна нулю вне этого круга. Притом, интеграл от h[i,j] по всей плоскости равен 1 (из этого условия выбираем константу const).

Рассмотрим действие такой системы на изображение, состоящее из одной точки на черном фоне (с произв коод).На изображение δ[i−m,j−n] (дельта-функция, сдвинутая в точку (m,n)) система отвечает изображением h[i-m,j-n] в силу инвариантности к сдвигу. Так, на единичные точки в любом месте система отвечает кругами радиуса 3 с центром в положении этих единичных точек. То есть любая точка как бы размывается в круг. В комп. графике импульсную характеристику линейной системы называют функцией «размытия» точки. Существуют и другие лин. системы(с другими h(n)), выполняющие другие задачи. Все эти линейные системы называются фильтрами.

Свертка.

Способы вычисления отклика системы на произвольное изображение:

1) Каждая точка сигнала превращается в функцию h (сдвинутую в нужную точку и умноженную на величину данной точки сигнала), а потом все эти функции складываются.

2) Вычисление значения каждой точки в результирующем сигнале как взвешенной сумму некоторого множества соседних точек исходного сигнала. Коэффициенты этой суммы совпадают с импульсной характеристикой линейной системы, развернутой относительно точки 0.

Операция получения результирующего сигнала по исходному называется сверткой: - для одномерного случая.

Любая линейная система осуществляет свертку входного сигнала со своей импульсной характеристикой. Это записывается так: y[n] = x[n]∗ h[n]. Импульсная характеристика h[n] также называется ядром свертки.

Рассмотрим, что происходит с сигналом конечной продолжительности, когда его сворачивают с конечным ядром свертки. Пусть сигнал x[n]≠0 только на [0; N-1], а h[n]≠0 на отрезке [–m₁; m₂], состоящем из M точек (M = m₁+m₂+1). Тогда при подстановке этих сигналов в уравнение свертки, мы получим сигнал y[n], который отличен от нуля на [-m₁; N −1+ m₂]. Так, длина результирующего сигнала равна N+M-1, т.е. сумме длин исходного сигнала и ядра свертки минус один.

Итак, операция свертки расширяет сигнал на M-1 точку, где M – длина ядра свертки.

Свойства свертки:

1. x[n]∗ y[n] = y[n]∗ x[n] (т.е. можно переставлять местами исходный сигнал и ядро свертки – это свойство редко используется на практике).

2. (x[n]∗ y[n]) ∗ z[n] = x[n]∗ ( y[n]∗ z[n]) (т.е. вместо того, чтобы проводить свертку по очереди в разных системах, можно получить систему с ядром ( y[n]∗ z[n]) , которая является суперпозицией систем y[n] и z[n]).

3. x[n]∗ y[n] + x[n]∗ z[n] = x[n]∗ ( y[n] + z[n])