Главная | Обратная связь

Приложение 8. Принцип максимума для дискретных систем

 

Постановка задачи.

Динамика дискретных систем описывается в пространстве состояний системой из m разностных уравнений первого порядка вида:

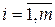(П.8.1)

где 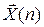- вектор переменных состояний разности 1 ´ m,

- вектор управления размерности 1 ´ r,

- известные функции,

Заданы начальные значения всех переменных состояние системы 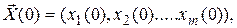область допустимых значений вектора управления 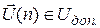и интервал управления n = 0 ¸ N. Могут быть дополнительно заданы конечные граничные условия системы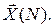

Необходимо на интервале управления системой n = 0 ¸ N так изменять элементы вектора управления чтобы обеспечился какой-либо из критериев оптимального управления, например, минимум интегральной целевой функции вида:

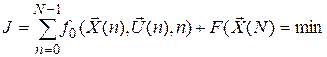, (П.8.2)

 

где F – терминальный член, характеризующий конечное состояние системы.

Если конечные граничные условия системы не заданы, то есть элементы вектора 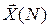неизвестны, то граничные условия для присоединенных функций определяются из условия трансверсальности:

(П.8.3)

Решение.

Функция Гамильтона для дискретных систем определяется по выражению:

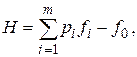(П.8.4)

 

где f₀ – известная функция, входящая в выражение для целевой функции,

f_i – известные функции, описывающие состояние системы,

p_i - присоединенные функции, определяемые из разностных уравнений первого порядка следующего вида:

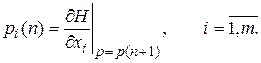(П.8.5)

Запись p = p(n + 1) означает, что в выражении все переменные записываются с номером цикла n , а переменные p_i с номером цикла n + 1.

Принцип максимума Понтрягина–Беллмана для дискретных систем. Он формулируется так: если вектор 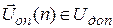оптимален в смысле поставленной оптимизационной задачи, то необходимым условием для этого является существование N векторов при которых частные производные

(П.8.6)

 

Тогда функция Гамильтона 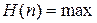в случае, если вектор лежит на границе допустимой области U_доп. Иначе говоря, оптимальный вектор

(П.8.7)

Выражение (П.8.7) следует понимать и читать так: оптимальный вектор управления являющийся аргументом функции Гамильтона, такой, который максимизирует функцию Гамильтона.

Если целевая функция J = max, то оптимальный вектор управления должен минимизировать функцию Гамильтона, то есть в этом случае:

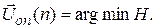
В отличие от сильного принципа максимума для непрерывных систем, принцип максимума Понтрягина–Беллмана для дискретных систем называют слабым принципом максимума. Причина состоит в том, что принцип максимума для дискретных систем является приближенным. Для дискретных систем доказана следующая теорема: оптимальный вектор управления в дискретных системах обращает в максимум функцию Гамильтона с погрешностью матрицы относительного дискретного времени 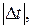то есть:

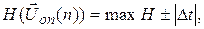
где: - диагональная матрица,

 

 

– относительная продолжительность цикла или такта в дискретных системах.

Очевидно, что чем меньше величина цикла T_ц по сравнению с общим интервалом управления T, тем меньше эта погрешность. При Dt ®0 дискретные системы превращаются в непрерывные, и погрешность принципа максимума для них стремится к нулю.

Пример 1. Затраты x₁ первого основного цеха завода от цикла к циклу описываются разностным уравнением первого порядка вида:

, (П.8.8)

а затраты x₂ второго (вспомогательного) цеха описываются разностным уравнением вида:

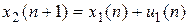(П.8.9)

Заданы начальное и конечное состояния системы 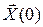и 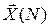и интервал управления системой n = 0 ¸ N.

Ставится задача: так изменять управление цехами u₁ и u₂ (изменять затраты), чтобы на интервале управления n = 0 ¸ N выполнялось условие минимума интегральной целевой функции

(П.8.10)

 

Эта функция учитывает затраты цехов x₁ и x₂ на каждом цикле, а также изменение затрат, вызванных величинами u₁ и u₂. Известно, что изменение объема производства в ту или иную сторону влечет увеличение потерь, связанных с перестройкой производства. Терминальная функция F в этой задаче равна нулю.

Решение. Вначале запишем выражение для функции Гамильтона с учетом (П.8.8), (П.8.9) и (П.8.10)

.

 

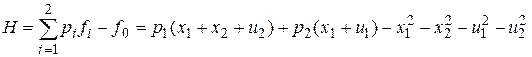Разностные уравнения, по которым вычисляются присоединенные функции p_i, определяются из выражения (П.8.5)

.

 

Применим это выражение при i = 1 и i = 2 для функции H и получим искомые выражения для присоединенных функций:

(П.8.11)

(П.8.12)

Оптимальное управление цехами u₁ и u₂ определяется из принципа максимума (П.8.7)

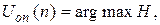
откуда следует формула (П.8.6), устанавливающая связь между элементами u_1оп и u_2оп оптимального вектора управления и переменными x_i и p_i

 

 

Применим это выражение при i = 1 и i = 2 для функции H и получим:

Из этих уравнений получим соотношения:

(П.8.13)

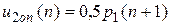(П.8.14)

Подставим их в (П.8.8), (П.8.9) и получим:

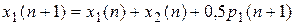(П.8.15)

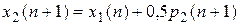(П.8.16)

Эти уравнения совместно с (П.8.11) и (П.8.12) описывают дискретную динамическую систему при оптимальном управлении.

Недостатком уравнений (П.8.11), (П.8.12), (П.8.15) и (П.8.16) является то, что первые два уравнения описывают процесс от конца к началу (номер цикла n убывает), а вторые два уравнения – от начала к концу.

Преобразуем их к одному виду, например, от конца к началу. В данной задаче направление безразлично, так как граничные условия переменных состояния x_i заданы и в начале и в конце процесса управления.

Из (П.8.16) имеем:

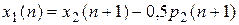. (П.8.17)

Вычтем (П.8.16) из (П.8.15) и получим:

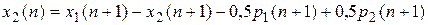. (П.8.18)

Подставим в (П.8.11) значение x₁(n) из (П.8.17) и получим:

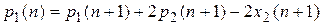. (П.8.19)

Подставим в (П.8.12) значение x₂(n) из (П.8.18) и получим:

. (П.8.20)

Уравнения (П.8.17), (П.8.18), (П.8.19) и (П.8.20) описывают динамическую систему от конца к началу при оптимальном уравнении. В данной задаче терминальная функция F не задана, и условием трансверсальности для определения граничных значений присоединенных функций p_i(N) воспользоваться нельзя.

Поэтому в данной задаче необходимо найти такие значения p_i(N), при которых от заданного конечного состояния системы 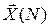надо перейти к заданному начальному состоянию системы 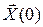по уравнениям (П.8.17) ¸ (П.8.20).

Для этого необходимо провести преобразование над указанными уравнениями на всех циклах процесса управления от n = N – 1 до n = 0 и выразить значения p_i(N) через известные значения элементов векторов 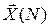и .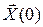

Сделаем эти преобразования при конкретных численных значениях N, 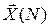и .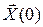

Пусть .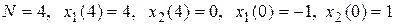

Тогда при n = 3 с учетом граничных условий на конце x₁(4) = 4 и x₂(4) = 0 из уравнений (П.8.17) ¸ (П.8.20) получим:

x₁(3) = - 0,5p₂(4)

x₂(3) = 4 - 0,5p₁(4) + 0,5p₂(4)

p₁(3) = p₁(4) + 2p₂(4)

p₂(3) = 2p₁(4) - 8 - p₂(4)

При n = 2 из уравнений (П.8.17) ¸ (П.8.20) получим:

x₁(2) = x₂(3) - 0,5p₂(3)

x₂(2) = x₁(3) - x₂(3) - 0,5p₁(3) + 0,5p₂(3)

p₁(2) = p₁(3) + 2p₂(3) - 2x₂(3)

p₂(2) = 2p₁(3) - 2x₁(3) + 2x₂(3) - p₂(3)

Подставим в эти уравнения значения x₁(3), x₂(3), p₁(3) и p₂(3), полученные при n =3 и, сделав необходимые арифметические вычисления, получим:

x₁(2) = 8 - 1,5p₁(4) + p₂(4)

x₂(2) = p₁(4) – 2,5p₂(4) - 8

p₁(2) = 6p₁(4) - p₂(4) - 24

p₂(2) = - p₁(4) + 7p₂(4) + 16

При n = 1 из уравнений (П.8.17) ¸ (П.8.20) получим:

x₁(1) = x₂(2) - 0,5p₂(2)

x₂(1) = x₁(2) - x₂(2) - 0,5p₁(2) + 0,5p₂(2)

p₁(1) = p₁(2) + 2p₂(2) - 2x₂(2)

p₂(1) = 2p₁(2) - 2x₁(2) + 2x₂(2) - p₂(2)

Подставим в эти уравнения значения x₁(2), x₂(2), p₁(2) и p₂(2), полученные при n = 2 и, сделав необходимые арифметические вычисления, получим:

x₁(1) = - 1,5p₁(4) - 6p₂(4) - 16

x₂(1) = - 6p₁(4) + 7,5p₂(4) + 36

p₁(1) = 2p₁(4) + 18p₂(4) + 24

p₂(1) = 18p₁(4) - 16p₂(4) - 96

При n = 0 вычислять значения p₁ и p₂ нет необходимости, поэтому определим только выражения для x₁(0) и x₂(0) по (П.8.17) и (П.8.18) при n = 0 с учетом результатов, полученных выше:

x₁(0) = - 15p₁(4) + 15,5p₂(4) + 84

x₂(0) = 15,5p₁(4) – 30,5p₂(4) - 112

Так как начальные граничные условия заданы: x₁(0) = -1, x₂(0) = 1, то после подстановки в эти выражения значений x₁(0) и x₂(0) получим систему из двух уравнений:

15p₁(4) - 15,5p₂(4) = 85

15,5p₁(4) – 30,5p₂(4) = 113

Решив эту систему, получим неизвестные значения присоединенных функций на конце процесса p₁(4) и p₂(4).

Решение этой системы дает следующие результаты:

p₁(4) = 3,872

p₂(4) = - 1,737

Подставив эти значения в уравнения (П.8.17) ¸ (П.8.20) при известных x₁(4) = 4 и x₂(4) = 0, определим значение x₁(3), x₂(3), p₁(3) и p₂(3). Снова подставим эти значения в (П.8.17) ¸ (П.8.20) и определим значения x₁(2), x₂(2), p₁(2) и p₂(2). Проделав эту процедуру до n = 0, определим все значения x₁(n), x₂(n), p₁(n) и p₂(n) на всем интервале управления. Отметим, что значения x₁(0) и x₂(0) должны совпасть с заданными значениями вектора 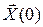с допустимой погрешностью. Элементы вектора оптимального управления определяются из соотношений (П.8.13) и (П.8.14).

В таблице П.8.1 приведены результаты вычислений по описанной процедуре. Здесь же приведены значения подынтегральной функции f₀ и значение целевой функции J, вычисленной по формуле (П.8.10).

Таблица П.8.1

 

n
x1	-1,0035	0,23	0,455	0,8685
x2	0,9945	-0,2595	-0,923	1,1955
p1	-	0,478	0,969	0,398	3,872
p2	-	1,488	-0,031	1,481	-1,737
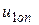
	0,744	-0,0155	0,7405	-0,8685	-
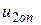
	0,239	0,4845	0,199	1,936	-
f0	2,610	0,355	1,647	6,686	J=11,2979

По табл. П.8.1 можно построить траектории процессов .

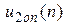Постановка задачи оптимального управления заводом, выпускающим бетон, при известном начальном состоянии и спросе на бетон на каждом цикле.

Необходимо на заданном интервале управления заводом n = 0 ¸ N так спланировать выпуск бетона при известном на него спросе, чтобы суммарные потери производителя и потребителей бетона (строительных организаций) от несовпадения спроса и предложения были минимальны.

Функция спроса бетона (в тыс. тонн) r(n) задана таблицей П.8.2.

Таблица П.8.2

n
r(n)

где n - номер цикла, например, номер дня недели,

r(n) - потребный раствор бетона, (тыс. тонн) по дням недели.

Процесс производства бетона описывается разностным уравнением вида:

x(n + 1) = x(n) + u(n), (П.8.21)

где u(n) - управление изменением объема производимого продукта. В этой задаче число m = 1.

Начальное условие x(0) = 1. Конечное условие x(N) не задано, N = 5.

Математически критерий оптимального управления заводом запишем в виде целевой функции, являющейся интегральной функцией потерь изготовителя и потребителей продукции:

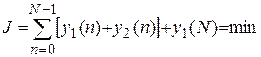, (П.8.22)

где функция

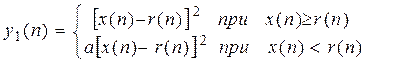(П.8.23)

 

 

отражает суммарные потери производителя и потребителей продукции от несовпадения спроса и предложения, когда разница x(n) - r(n) 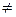0, причем при x(n) < r(n) эти потери больше, чем при x(n) > r(n), т.к. простои строителей обходятся дороже.

Функция y₂(n) = bu²(n) (П.8.24)

описывает потери производителя, связанные с изменением объема производства.

Решение задачи оптимального управления бетонным заводом осуществляется следующим образом. Пусть a = 2, b = 3.

Функция Гамильтона на основании (П.8.4) с учетом (П.8.24) и (П.8.22) имеет вид:

H = p(x + u) - y₂ - y₁ ,

а с учетом (П.8.23) и (П.8.24) получим:

 

 

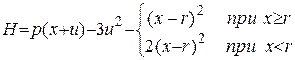
Выражение для присоединенной функции определим по формуле (П.8.5)

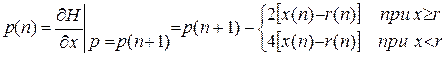(П.8.25)

 

Выражение для оптимального управления заводом определяется по (П.8.6)

р(n + 1) - 6u_оп(n) = 0 , откуда

. (П.8.26)

Подставим это выражение в (П.8.21) и получим:

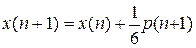, откуда

. (П.8.27)

 

Чтобы сделать расчеты по этому уравнению, надо знать x(N) и p(N).

Для определения p(N) воспользуемся условием трансверсальности (П.8.3)

.

 

Из (П.8.22) на основании (П.8.2) и (П.8.23) следует, что в данном случае терминальный член:

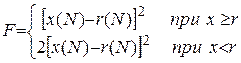
Тогда (П.8.28)

 

Так как значение x(N) неизвестно, то определить значение p(N) аналитически не представляется возможным.

В ситуациях, подобных данной, когда число граничных условий меньше числа разностных уравнений, а условием трансверсальности воспользоваться нельзя, решить задачу можно методом перебора. Суть метода в следующем. Вначале зададим наугад значение x(N). По здравому смыслу оно не должно сильно отличаться от r(N) = r(5) = 8. Затем по выражению (П.8.28) определим величину p(N) = p(5). Далее по выражению (П.8.27) определим величину x(4), а по выражению (П.8.25) определим p(4).

Далее повторим этот процесс вычислений по формулам (П.8.27) и (П.8.25) при n = 3 и определим x(3) и p(3).

Далее повторим процесс вычислений по формулам (П.8.27) и (П.8.25) при n = 2, n = 1 и n = 0. В результате определим значение x(0).

Теперь сравним его с заданным начальным условием x(0). Если разница между рассчитанным и заданным значением x(0) по модулю меньше числа e ® 0, то мы угадали величину x(N). В противном случае снова вернемся к началу вычислений, зададимся другим значением x(N) и повторим процесс вычислений снова. И так до тех пор, пока не получится заданная величина x(0) с погрешностью e. После этого по (П.8.27) и (П.8.25) рассчитывается весь процесс от n = 5 до n = 0. Величину 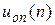рассчитываем по (61).

Описанную процедуру решения задачи методом перебора можно выполнить быстро, если запрограммировать разностные уравнения (П.8.28), (П.8.27) и (П.8.25) на ЭВМ.

Результаты решения задачи оптимального управления бетонным заводом приведены в таблице П.8.3.

Таблица П.8.3

n
x		1,9025	2,7402	4,1578	5,0142	6,2085
uоп	0,9025	0,8376	1,4176	0,8562	1,1943	-
f0	2,4435	2,1237	9,057	3,6178	5,3076	6,4189	J=28,9686

 

На рис. П.8.1 приведены зависимости x(n) и r(n), построенные по табл. П.8.2 и табл. П.8.3.

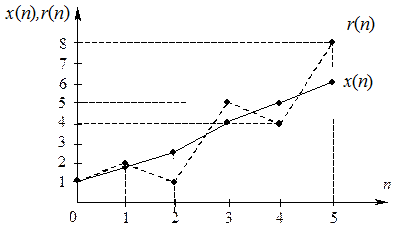
Рис. П.8.5. Зависимости x(n) и r(n)

Из этого рисунка видно, что функция оптимального предложения товара x(n) представляет собой сглаженный процесс от функции спроса r(n).