 |
|
Использование способа парной корреляции для изучения стохастических зависимостей
В анализе используются парная и множественная корреляции.
Парная корреляция – это корреляционная зависимость между двумя признаками.
Простейшим уравнением, которое характеризует прямолинейную зависимость между двумя признаками, является уравнение прямой линии
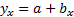
где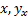 
– соответственно независимый и зависимый признаки уравнения;
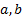– параметры уравнения регрессии.
Количество наблюдений при прямолинейной зависимости должно быть не менее шести (годы, предприятия или цехи).
В качестве примера прямолинейной зависимости используются данные об изменении фондовооруженности и производительности труда работающих, приведенные в табл. 8.1.
Таблица 8.1 
Исходные данные и вспомогательные расчеты для определения зависимости между фондовооруженностью и производительностью труда работающих
| Годы, месяцы | Производительность труда работающих у, тыс. р. | Фондовооруженность работающих х, тыс. р. | ху | х2 | у2 |
| 6,2 | 1,6 | 9,9 | 2,6 | 38,4 | |
| 6,6 | 1,8 | 11,9 | 3,2 | 43,6 | |
| 6,9 | 2,0 | 13,8 | 4,0 | 47,6 | |
| 6,8 | 2,0 | 13,6 | 4,0 | 46,2 | |
| 7,3 | 2,3 | 16,8 | 5,3 | 53,3 | |
| 7,6 | 2,4 | 18,2 | 5,8 | 57,8 | |
| 8,6 | 2,5 | 21,5 | 6,3 | 74,0 | |
| 9,1 | 2,6 | 23,7 | 6,8 | 82,8 | |
| 10,6 | 2,6 | 27,6 | 6,8 | 112,4 | |
| 11,2 | 2,8 | 31,4 | 7,8 | 125,4 | |
| Итого | 80,9 | 22,6 | 188,4 | 52,6 | 681,5 |
При планировании роста производительности труда важно определить ее повышение в зависимости от увеличения фондовооруженности.
Связь между производительностью и фондовооруженностью труда можно выразить в виде уравнения прямой линии
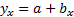
где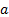 
– постоянная величина, не связанная с изменением данного фактора.
Для выяснения связи рассчитаем коэффициент корреляции по формуле
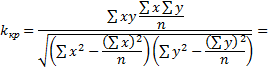
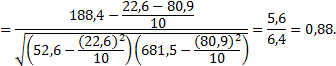
Коэффициент корреляции 0,88 выражает связь между фондовооруженностью и производительностью труда и по абсолютной величине может принимать значения в пределах от нуля до единицы. Если никакой связи между двумя изучаемыми показателями нет, то он будет равен нулю. Если же между исследуемыми признаками существует тесная связь, то коэффициент корреляции близок к единице.
Если коэффициент корреляции равен единице, значит, результативный признак полностью зависит от признака-фактора, т.е., по существу, корреляционная зависимость совпадает с функциональной. Следовательно, чем ближе коэффициент корреляции к единице, тем теснее связь между изучаемыми явлениями и наоборот.
Для нахождения неизвестных параметров а в решаем систему так называемых нормальных уравнений:
.
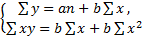Величина 
определяется умножением значений 
и 
и последующим суммированием полученного произведения. Для исчисления величины 
следует значения возвести в квадрат и полученные результаты суммировать.
Числовые значения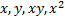 
рассчитываются на основании фактических исходных данных, представленных в табл. 8.1.
В результате подстановки данных табл. 8.1. в систему уравнений получаем:
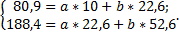
Из данной системы уравнений получаем:
Уравнение, отражающее связь между фондовооруженностью и производительностью работающих, имеет следующий вид:
Следовательно, увеличение фондовооруженности труда работающих на 1000 р. приводит к росту производительности труда на 912 р. Эти данные учитываются при перспективном и текущем планировании повышения производительности труда.