Главная | Обратная связь

Задачи линейного программирования(ЛП). Регуляризация задач ЛП.

При оптимизации экономических планов возникают задачи на минимум линейной функции n переменных при наличии линейных дополнительных условий 3-ёх типов:

L(x)= = min, (1)

, , (2)

, , (3)

, m , (4)

усл. (2) или (4) определяют полупространство, ограниченное гиперплоскостью, все эти усл. определяют выпуклый n-мерный многогранник J , кот. явл. пересечением соотв. полупр-в. С математической точки зрения эти усл. однотипны. Усл.(3) выделяют из n-мерного пр-ва (n-m)-мерную плоскость. Её пересечение с областью J даёт выпуклый (n-m)-мерный многогранник G, наша задача в том, чтобы найти минимум линейной ф-ии (1) в этом многограннике G.

Примером такой задачи явл. распределение производства однотипной продукции по разным заводам.

– выпускаемое i-ым заводом кол-во продукции ( )

- себестоимость 1-го изделия на этом заводе.

- при j>m - расход сырья j-го вида

при 2 - расход зарплаты и др. аналог. показатели

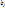- суммарный выпуск продукции по всем заводам.

(4) – расход сырья по всем заводам, а L – себестоимость общей продукции.

X – удовл. всем дополнит. усл. , наз. планом, решение(1)-оптимальным планом. А – вектор усл., В – вектор огр.

Приведём задачу к каноническому виду, для этого введём в качестве новых переменных невязки усл. 3-го типа:

, n<i , N=n+M-m (5)

Доопределим коэфф. (1) следующим образом:

, при n<i , 1 . (6)

Каноническая форма з. ЛП:

Многогранник канонических усл. образован пересечением новой (N-M)-мерной пл-ти усл. с первым координ. углом. Значит у вершины часть координат – нули, а остальные >0.

Строки новой м-цы А линейно-независимы. Все ЛНЗ наборы столбцов А соотв. точкам пересечения пл-ти усл. с координатными гиперплоскостями.

Далее перенумеруем переменные так, чтобы первыми были базисные переменные

, (10)

, 1 , i M эл-ты м-цы, обратной к базисной квадратной м-це, стоящей в левой части с-мы (1). Приравнивая внебазисные корд. к нулю и решая с-му, получим коорд. точки пересечения пл-ти усл. с корд. гиперплоскостью.

(11)

Если найденные координаты неотрицательны, то точка явл. вершиной многогранника канонических усл. Если хотя бы 1 <0 , эту точку надо отбросить и исследовать другой набор столбцов м-цы А . Если забракованы все точки, то это значит, что усл. 1-го и 2-го рода образуют несовместную с-му.

Различные столбцы А могут образовывать наборов. Поэтому в самом неблагоприятном случае (M N) è вершин. Если N 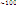, то простой перебор вершин невозможен.

2)Регуляризация задач ЛП.

Задача ЛП часто оказывается плохо обусловленной . поэтому не удаётся даже проверить, может ли реш. поставленной задачи.

Для регуляризации задач ЛП будем искать нормальное реш. х, т.е. наименее уклоняющееся от некоторого заданного х₀ (х₀- ранее составленный план)

Возьмём (7). Дополнительное усл Ах=b, вводим штрафную ф-ию ²

²=min, >0 (12)

Норма определяется как

Усл. близости реш. к заданному вектору можно считать малость или малость величины

[x]= ² , >0 (13)

Эту величину можно считать штрафом и прибавлять в качестве дополнит. слагаемого в левую часть (12), тогда получаем регуляризованную задачу:

M[x]= ²+ 𝝀𝜴[x]=min , 𝝀, >0 (14)

При решении (14) усл. неотрицательности можно не принимать во внимание M[x] – квадратичная форма, поэтому нахождение min сводится к решению с-мы линейных у-ий. Т.к. задача регуляризованна, то линейная с-ма будет хорошо обусловлена, тогда её реш. при большом числе неизв. N легко вычислить методом исключения Гаусса. Более сложно выбрать параметры регуляризации 𝝀, подбирают так чтобы выполнялось усл. 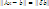, где -допустимая погр. выч., т.к. его компоненты и коэф. А известны неточно.Аналогично 𝝀 связывают с погр. и с допустимыми отклон. L(x) от min.

При численном реш. (14) приходится находить серию регуляриз. реш., соотв. разным знач. 𝝀 и и выбирать оптимальные параметры.