Главная | Обратная связь

Восстановление функций по МНК.

На практике мы часто сталкиваемся с задачей о сглаживании экспериментальных зависимостей.

Пусть зависимость между двумя переменными x и y выражается в виде таблицы, полученной опытным путем. Это могут быть результаты опыта или наблюдений, статистической обработки материала и т.п.

Требуется наилучшим образом сгладить экспериментальную зависимость между переменными x и y, т.е. по возможности точно отразить общую тенденцию зависимости y от x, исключив при этом случайные отклонения, связанные с неизбежными погрешностями измерений или статистических наблюдений. Такую сглаженную зависимость стремятся представить в виде формулы y=f(x).

Формулы, служащие для аналитического представления опытных данных, получили название эмпирических формул. Задача нахождения эмпирических формул разбивается на два этапа. На первом этапе нужно установить вид зависимости y=f(x), т.е. решить, является ли она линейной, квадратичной, логарифмической или какой-либо другой. Второй этап – определение неизвестных параметров этой функции.

Часто вид эмпирической зависимости известен, но числовые параметры неизвестны. Будем считать, что зависимость полиномиальная, а для определения параметров полинома рассмотрим следующий метод.

Метод наименьших квадратов. Пусть функция y=f(x) задана таблицей своих значений: Требуется найти многочлен фиксированной степени m для которого среднеквадратичное отклонение (СКО)

минимально.

Так как многочлен

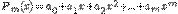определяется своими коэффициентами, то фактически нужно подобрать набор коэффициентов 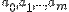минимизирующий функцию

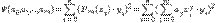
Используя необходимое условие экстремума, 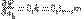получаем так называемую нормальную систему метода наименьших квадратов:

Полученная система есть система алгебраических уравнений относительно неизвестных a₀,a₁..a_m. Можно показать, что определитель этой системы отличен от нуля, то есть решение существует и единственно. Однако при высоких степенях m система является плохо обусловленной. Поэтому метод наименьших квадратов применяют для нахождения многочленов, степень которых не выше 5. Решение нормальной системы можно найти, например, методом Гаусса. Запишем нормальную систему наименьших квадратов для двух простых случаев:m=0 и m=2. При m=0 многочлен примет вид: P₀(x)=a₀. Для нахождения неизвестного коэффициента a₀ имеем уравнение:

_.

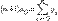Получаем, что коэффициент a₀ есть среднее арифметическое значений функции в заданных точках.

Если же используется многочлен второй степени то нормальная система уравнений примет вид: