Главная | Обратная связь

Вращающееся магнитное поле двухфазного тока.

Рассмотрим образование вращающегося магнитного поля на примере двухфазного синусоидального тока и двух катушек, сдвинутых в пространстве одна относительно другой на угол 90°.

Катушка 1 создает магнитное поле, силовые линии которого перпендикулярны ее плоскости. На рис. 8.1 это магнитное поле представлено вектором магнитной индукции 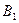. Магнитное поле катушки 2 характеризуется вектором магнитной индукции . К катушке 1 подводится синусоидальный ток , к катушке 2 — ток

Индукция магнитного поля пропорциональна создающему его току; следовательно

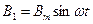
Магнитные поля катушек, налагаясь друг на друга, образуют результирующее поле. Модуль вектора индукции результирующего магнитного поля определим из векторной диаграммы по теореме Пифагора:

Таким образом, индукция результирующего магнитного поля оказывается не зависящей от времени величиной, равной максимальному значению индукции поля одной катушки. Это значит, что магнитные поля первой и второй катушек меняются так согласованно, что результирующее поле остается постоянным по значению.

Направление силовых линий результирующего магнитного поля характеризуется направлением вектора В, который образует угол а с горизонтальной осью, определяемой из выражения

Отсюда 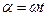, т. е. вектор В вращается против часовой стрелки с угловой скоростью ω, равной угловой скорости синусоидального тока.

Результирующее магнитное поле катушек можно представить как поле постоянного магнита, который поворачивается в пространстве (рис. 8.2). Твкое поле называют вращающимся. Нетрудно убедиться, что результирующее магнитное поле катушек будет вращаться в обратную сторону, если поменять фазы токов

Графическое пояснение процесса образования вращающегося магнитного поля. Изобразим графически с помощью магнитных силовых линий поле двух рассмотренных катушек.

На рис. 8.3 схематически изображен цилиндрический магнитопровод, в пазах которого размещены катушки АХ и BY. Буквами А и В обозначены начала, и Y — концы катушек. По катушке АХ проходит ток , изменяющийся по синусоидальному закону, по катушке BY — ток , изменяющийся по косинусоидальному закону. Будем считать положительным ток, проходящий от начала катушки к ее концу.

При t = 0 ток в катушке АХ отсутствует, а ток в катушке BY положителен. Силовые линии, определенные по правилу буравчика, выходят из верхней части магнитопровода и направлены в нижнюю часть аналогично силовым линиям постоянного магнита, изображенного справа, у которого северный полюс расположен вверху, а южный — внизу.

При 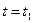ток , а ток 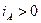. Силовые линии магнитного поля токов аналогичны силовым линиям постоянного магнита, у которого северный полюс расположен слева, а южный — справа.

При 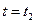ток , а ток . В этом случае силовые линии магнитного поля токов аналогичны силовым линиям постоянного магнита, у которого северный полюс расположен внизу, а южный — вверху.

Продолжив рассмотрение процессов изменения токов и магнитных потоков для других моментов времени, нетрудно убедиться, что за половину периода тока магнитное поле повернется на 180°, а за период сделает полный оборот. Следовательно, число оборотов вращающегося магнитного поля р секунду равно частоте тока f.

Частоту вращения магнитного поля принято выражать числом оборотов в минуту. Тогда .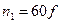

Чтобы понять принцип получения многополюсных вращающихся полей, обратимся к рис. 8.4. Здесь схематически изображен магнитопровод, разделенный на две половины, в каждой из которых размещены катушки АХ и BY. Таким образом, устройство имеет две катушки АХ, через которые проходит ток , и две катушки ВY, через которые проходит ток .

Проводя аналогичные рассуждения, устанавливаем, что магнитное поле токов аналогично полю четырехполюсного постоянного магнита, причем в течение половины периода тока поле делает только четверть оборота, а полный оборот совершает за два периода. Таким образом, если в два раза увеличить число пар полюсов, то частота вращения поля уменьшится в два раза. Легко показать, что увеличение числа пар полюсов в три раза уменьшило бы частоту вращения поля в три раза, т. е. в общем случае 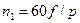, где р — число пар полюсов. При р=1 эта формула совпадает с предыдущей,

Вращающееся магнитное поле трехфазного тока. Для создания вращающегося магнитного поля с помощью трехфазной системы токов нужны три катушки, сдвинутые в пространстве на 120° одна относительно другой (рис. 8.5).

Магнитная индукция, создаваемая при этом каждой катушкой, пропорциональна соответствующему току:

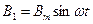
Выберем произвольное направление, повернутое на угол α относительно вектора магнитной индукции 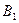(пунктирная ось), и найдем вектор результирующей магнитной индукции в этом направлении. С этой целью сложим проекции векторов 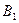, , на выбранное направление:

Подставим в это соотношение выражения для , , :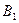

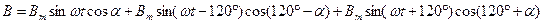
После тригонометрических преобразований получим:

Синусоидально изменяющиеся величины в последней квадратной скобке можно представить системой векторов, изображенной на рис. 8.6. Нетрудно убедиться, что сумма

этих векторов равна нулю. Таким образом, . Пусть угол (см. рис. 10.5)

Тогда . При 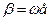получим , т. е. магнитная индукция вдоль оси XX максимальна, а сама ось XX вращается с угловой частотой со.

Направление вращения поля определяется порядком следования фаз. Для изменения направления вращения поля достаточно поменять местами любые две фазы из трех.

В заключение отметим, что для получения неискаженного вращающегося магнитного поля система катушек должна быть полностью симметричной, а токи должны быть строго одинаковыми по амплитуде и частоте и сдвинутыми по фазе на 120° один относительно другого.