 |
|
Исследование функций методами
Дифференциального исчисления
Интервалы монотонности функции
Функция называется возрастающей (убывающей) в некотором интервале, если в этом интервале каждому большему значению аргумента соответствует большее (меньшее) значение функции.
Как возрастающие, так и убывающие функции называются монотонными. Монотонность функции  характеризуется знаком первой производной
характеризуется знаком первой производной  . Если в некотором интервале
. Если в некотором интервале  >0 (
>0 (  <0), то функция возрастает (убывает) в этом интервале.
<0), то функция возрастает (убывает) в этом интервале.
Рассмотрим примеры.
1. Даны функция 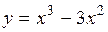 и точки
и точки  . В каких из перечисленных точек функция возрастает? Убывает?
. В каких из перечисленных точек функция возрастает? Убывает?
Решение.
Найдем производную заданной функции: 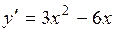 .
.
При 
 >0 - функция возрастает,
>0 - функция возрастает,
при 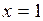
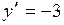 <0 - функция убывает,
<0 - функция убывает,
при 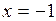
 >0 - функция возрастает,
>0 - функция возрастает,
при 
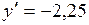 <0 - функция убывает.
<0 - функция убывает.
2. Найти интервалы возрастания и убывания функции  , если
, если 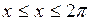 .
.
Решение.
Найдем производную заданной функции:  . В промежутке
. В промежутке  производная
производная 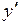 >0 поэтому функция возрастает, а в промежутках
>0 поэтому функция возрастает, а в промежутках  и
и 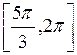 производная
производная 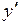 <0 – функция убывает.
<0 – функция убывает.
3. Определить характер монотонности функции  в промежутке
в промежутке 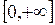 .
.
Решение.
Найдем производную: 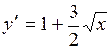 . При
. При 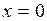 производная
производная 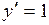 >0 функция возрастает. При
>0 функция возрастает. При  производная
производная  >0 – функция возрастает. Следовательно, функция возрастает во всей области определения.
>0 – функция возрастает. Следовательно, функция возрастает во всей области определения.
Решить следующие задачи.
Убедиться, что функция 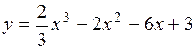 в интервале
в интервале 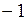 <
< 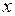 <3 убывает.
<3 убывает.
Определить интервалы убывания и возрастания функции 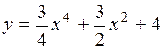 . (Ответ: при x<0 функция убывает, при x>0 - возрастает.)
. (Ответ: при x<0 функция убывает, при x>0 - возрастает.)
Определить, при каких значениях 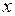 функция
функция 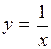 убывает.
убывает.
(Ответ: при любом 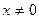 функция убывает).
функция убывает).
Проверить, во всем ли интервале  функция
функция 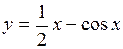 возрастает. (Ответ: при
возрастает. (Ответ: при  функция убывает).
функция убывает).
Определить интервал возрастания функции 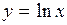 . (Ответ: при x>0 функция возрастает).
. (Ответ: при x>0 функция возрастает).
Найти интервалы возрастания и убывания функции 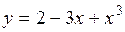 . (Ответ: в интервале
. (Ответ: в интервале 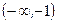 и
и 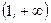 функция возрастает; в интервале
функция возрастает; в интервале 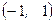 - убывает).
- убывает).
Найти интервалы монотонности функции 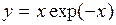 . (Ответ: интервал возрастания
. (Ответ: интервал возрастания 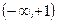 , интервал убывания
, интервал убывания 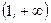 )
)
Экстремум функции
Точка 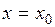 называется точкой максимума (минимума) функции
называется точкой максимума (минимума) функции  , если существует такая окрестность точки
, если существует такая окрестность точки 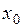 , что для всех
, что для всех 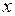
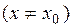 этой окрестности выполняется неравенство
этой окрестности выполняется неравенство  <
< 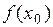 (максимум) или
(максимум) или  >
> 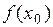 (минимум).
(минимум).
Точки максимума и минимума функции называются точками ее экстремума, а значение функции в точке максимума (минимума) – максимумом (минимумом), или экстремумом функции.
Правило отыскания экстремумов функции:
1. Вычислить производную  .
.
2. Составить уравнение  =0 и найти его корни, которые являются критическими точками функции.
=0 и найти его корни, которые являются критическими точками функции.
3. Установить знак производной  слева и справа от критической точки.
слева и справа от критической точки.
Если при переходе через критическую точку производная меняет знак с плюса на минус (вторая производная при этом меньше нуля), то в критической точке она имеет максимум.
Если производная в критической точке меняет знак с минуса на плюс (вторая производная при этом больше нуля), то функция в этом точке имеет минимум.
Рассмотрим примеры.
1. Исследовать на экстремум функцию  .
.
Решение.
Находим первую производную заданной функции: 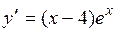 . Приравниваем ее нулю и определяем критические точки:
. Приравниваем ее нулю и определяем критические точки:  , значение
, значение 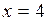 является критической точкой. Определяем знак
является критической точкой. Определяем знак  при переходе через критическую точку. Если
при переходе через критическую точку. Если  , то
, то 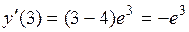 <0. Если
<0. Если 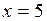 , то
, то  >0. Полученный результат позволяет утверждать, что в точке
>0. Полученный результат позволяет утверждать, что в точке 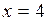 функция имеет минимум, значение которого
функция имеет минимум, значение которого 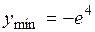 .
.
2. Исследовать на экстремум функцию 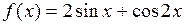 .
.
Решение.
Так как  - периодическая функция с периодом
- периодическая функция с периодом 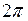 , то достаточно найти экстремумы на отрезке
, то достаточно найти экстремумы на отрезке 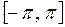 .
.
Дифференцируя, получим 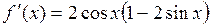 . Производная существует на всем отрезке
. Производная существует на всем отрезке 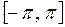 и обращается в нуль в точках
и обращается в нуль в точках  . Для исследования функции на экстремум выясним знак второй производной
. Для исследования функции на экстремум выясним знак второй производной  в каждой из полученных точек. Имеем:
в каждой из полученных точек. Имеем:
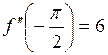 >0; >0;
| 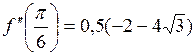 <0; <0;
|  >0; >0;
| 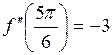 <0. <0.
|
Отсюда следует, что
при   ; ;
| при   ; ;
|
при 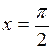 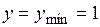 ; ;
| при   . .
|
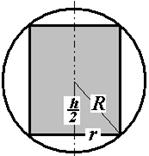 Рис. 1 Рис. 1
|
3. В шар радиусом R вписан цилиндр наибольшего объема. Обозначим высоту, радиус основания и объем цилиндра соответственно через  . Объем цилиндра рассчитывается по формуле
. Объем цилиндра рассчитывается по формуле 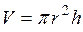 . Из геометрических построений видно (рис. 1), что
. Из геометрических построений видно (рис. 1), что  , тогда формула для расчета объема будет иметь вид
, тогда формула для расчета объема будет иметь вид  .
.
Таким образом, задача сводится к нахождению наибольшего значения функции  в промежутке
в промежутке 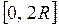 .
.
Найдем производную:  . Приравнивая нулю
. Приравнивая нулю 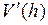 , получим единственную критическую точку
, получим единственную критическую точку 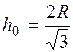 , принадлежащую рассматриваемому промежутку
, принадлежащую рассматриваемому промежутку 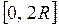 , в которой объем и принимает наибольшее значение
, в которой объем и принимает наибольшее значение  .
.
В итоге мы получили, что наибольший объем будет иметь цилиндр, высота которого 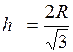 .
.
4. На какой высоте  над центром круглого стола радиусом R следует поместить электрическую лампочку, сила света которой J, чтобы освещенность E края стола была максимальной?
над центром круглого стола радиусом R следует поместить электрическую лампочку, сила света которой J, чтобы освещенность E края стола была максимальной?
Решение.

|
Освещенность вычисляется по формуле 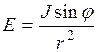 , где значения
, где значения  и
и 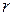 определяются, исходя из рис.2.
определяются, исходя из рис.2.
За независимую переменную примем угол  и,
и,
| Рис. 2 |
учтя, что  , получим
, получим
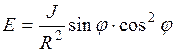 .
.
Найдем максимальное значение полученной функции в промежутке  изменения независимой переменной
изменения независимой переменной  . Дифференцируя
. Дифференцируя 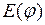 , получим
, получим  . Решая уравнение
. Решая уравнение 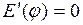 , находим, что функция
, находим, что функция 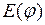 в интервале
в интервале  имеет единственную критическую точку:
имеет единственную критическую точку: 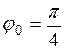 . Следовательно, при
. Следовательно, при 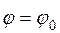 освещенность
освещенность 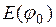 будет наибольшей, поэтому
будет наибольшей, поэтому 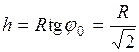 . Это и есть искомая величина.
. Это и есть искомая величина.
Исследовать на экстремум следующие функции.
3.8. 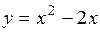 . (Ответ: при
. (Ответ: при  функция имеет минимум).
функция имеет минимум).
3.9. 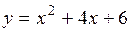 . (Ответ: при
. (Ответ: при  функция имеет максимум).
функция имеет максимум).
3.10. 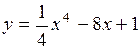 . (Ответ: при
. (Ответ: при  функция имеет минимум).
функция имеет минимум).
3.11. 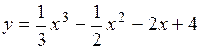 .
.
(Ответ: при 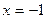 функция имеет максимум, при
функция имеет максимум, при  - минимум).
- минимум).
3.12. 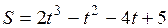 .
.
(Ответ: при 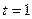 функция имеет минимум, при
функция имеет минимум, при  - максимум).
- максимум).
3.13.  . (Ответ: при
. (Ответ: при  функция имеет минимум).
функция имеет минимум).
3.14. 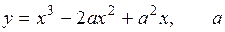 >0.
>0.
(Ответ: при 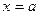 функция имеет минимум, при
функция имеет минимум, при  - максимум).
- максимум).
Исследовать функцию 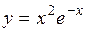 на экстремум и найти значения функции в экстремальных точках. (Ответ: при
на экстремум и найти значения функции в экстремальных точках. (Ответ: при 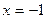 функция имеет минимум;
функция имеет минимум; 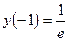 ).
).
Секундный расход воды  при истечении ее через отверстие в толстой стене определяется по формуле
при истечении ее через отверстие в толстой стене определяется по формуле 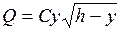 , где
, где 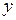 - диаметр отверстия,
- диаметр отверстия,  - глубина его низшей точки,
- глубина его низшей точки,  - некоторая постоянная. При каком значении
- некоторая постоянная. При каком значении 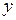 секундный расход воды
секундный расход воды  является наибольшим? (Ответ: при
является наибольшим? (Ответ: при 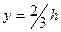 ).
).
Показать, что мощность 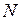 тока, получаемого от гальванического элемента во внешней цепи, будет наибольшей, если сопротивление R внешней цепи равно внутреннему сопротивлению
тока, получаемого от гальванического элемента во внешней цепи, будет наибольшей, если сопротивление R внешней цепи равно внутреннему сопротивлению 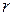 самого элемента.
самого элемента.
Тело брошено вертикально вверх с начальной скоростью 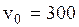 м/с. Уравнение движения тела
м/с. Уравнение движения тела 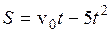 . Будет ли тело подниматься или опускаться в момент
. Будет ли тело подниматься или опускаться в момент 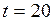 с? В какой момент оно достигнет максимальной высоты и какова эта высота? (Ответ: тело поднимается; максимальной высоты достигнет в момент времени
с? В какой момент оно достигнет максимальной высоты и какова эта высота? (Ответ: тело поднимается; максимальной высоты достигнет в момент времени 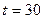 с;
с;  м).
м).
Рост численности популяции в условиях ограниченности ресурсов происходит по закону  , где
, где 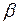 - постоянная величина, зависящая от вида клеток, характера среды и других внешних факторов;
- постоянная величина, зависящая от вида клеток, характера среды и других внешних факторов;  и
и  - начальная и максимально возможная численность популяции. Определить момент времени, когда скорость роста популяции максимальна, и численность популяции в этот момент. (Ответ:
- начальная и максимально возможная численность популяции. Определить момент времени, когда скорость роста популяции максимальна, и численность популяции в этот момент. (Ответ:  ;
; 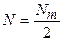 ).
).
В последовательной реакции  концентрация промежуточного вещества
концентрация промежуточного вещества  зависит от времени по закону
зависит от времени по закону 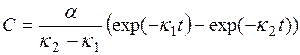 , где
, где 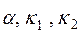 - постоянные величины (
- постоянные величины (  >
> 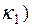 . Определить скорость изменения концентрации. Через какое время после начала реакции концентрация достигнет максимума? (Ответ:
. Определить скорость изменения концентрации. Через какое время после начала реакции концентрация достигнет максимума? (Ответ: 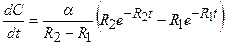 ;
; 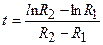 ).
).
В шар радиусом R вписан цилиндр, имеющий наибольшую боковую поверхность. Определить высоту цилиндра. (Ответ: высота равна 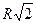 ).
).
ГЛАВА 4
НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ[4]
§1. Непосредственное интегрирование.
Функция  называется первообразной для функции
называется первообразной для функции  , если
, если

или
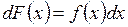 .
.
Любая непрерывная функция  имеет бесконечное множество первообразных, которые отличаются друг от друга постоянным слагаемым С.
имеет бесконечное множество первообразных, которые отличаются друг от друга постоянным слагаемым С.
Совокупность  всех первообразных для функции
всех первообразных для функции  называется неопределенным интегралом от этой функции:
называется неопределенным интегралом от этой функции: