 |
|
Теплоемкость, коэффициент Пуассона
Количество теплоты Q, необходимое для нагревания массы однородного вещества от температуры  до температуры
до температуры  , пропорционально массе вещества и изменению температуры
, пропорционально массе вещества и изменению температуры
 , ,
| (1) |
где c – удельная теплоемкость вещества. Из формулы (1) следует
 . .
|
Как видно, удельной теплоемкостью вещества называется количество теплоты, необходимое для повышения температуры вещества массой 1 кг на 1 К.
Теплоемкостью тела называют количество теплоты, необходимое для повышения его температуры на 1 К.
 . .
|
Молярной теплоемкостью называют количество теплоты, необходимое для повышения температуры 1 моля вещества на 1 К.
 , ,
|
где  – количество молей вещества, M – молярная масса вещества. Из определения удельной теплоемкости следует, что она связана с молярной теплоемкостью соотношением
– количество молей вещества, M – молярная масса вещества. Из определения удельной теплоемкости следует, что она связана с молярной теплоемкостью соотношением
 . .
|
Состояние газа может быть охарактеризовано тремя величинами – давлением p, объемом V и температурой T. Уравнение, связывающее эти величины, называют уравнением состояния вещества. Для идеального газа уравнением состояния является уравнение Менделеева-Клайперона, которое имеет вид
 , ,
| (2) |
где R – универсальная газовая постоянная.
Величина теплоемкости газов зависит от условий нагревания. Для выяснения этой зависимость, необходимо воспользоваться уравнением состояния (2) и первым началом термодинамики, которое можно сформулировать следующим образом:
количество теплоты  , переданное системе, затрачивается на увеличение ее внутренней энергии
, переданное системе, затрачивается на увеличение ее внутренней энергии  и на работу
и на работу 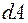 , совершаемую системой против внешних сил
, совершаемую системой против внешних сил
 .
.
Воспользовавшись определением молярной теплоемкости, получим
 , ,
| (3) |
Из формулы (3) видно, что теплоемкость может иметь различные значения в зависимости от способа нагревания газа, так как одному и тому же значению  могут соответствовать различные значения
могут соответствовать различные значения  и
и 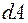 .
.
Внутренняя энергия идеального газа – это энергия теплового движения молекул и атомов в молекулах. Она складывается из кинетических энергий поступательного и вращательного движения молекул и энергии колебаний атомов в них. Согласно закону равнораспределения энергии по степеням свободы молекулы, на каждую поступательную и вращательную степень свободы молекулы приходится в среднем энергия, равная  , где k – постоянная Больцмана, а на каждую колебательную степень свободы – энергия, равная kT. Таким образом, средняя энергия теплового движения молекулы идеального газа равна
, где k – постоянная Больцмана, а на каждую колебательную степень свободы – энергия, равная kT. Таким образом, средняя энергия теплового движения молекулы идеального газа равна
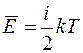 ,
,
где i – число степеней свободы молекулы. Числом степеней свободы молекулы называют число независимых координат, определяющих положение молекулы в пространстве.
Внутренняя энергия n молей газа равна
 .
.
Отсюда следует, что внутренняя энергия данного количества идеального газа зависит от его абсолютной температуры, но не зависит от объема, что является следствием модели идеального газа, в которой потенциальной энергией межмолекулярного взаимодействия пренебрегают.
Изменение внутренней энергии газа определяется формулой
 .
.
Рассмотрим основные процессы, протекающие в идеальном газе:
1. Изохорический процесс.
Процесс называется изохорическим, если объем газа при изменении температуры остается неизменным. В этом случае  , а следовательно
, а следовательно  (элементарная работа газа
(элементарная работа газа  ), то есть вся подводимая к газу теплота идет на увеличение его внутренней энергии. Тогда из уравнения (3) следует, что молярная теплоемкость газа при постоянном объеме равна
), то есть вся подводимая к газу теплота идет на увеличение его внутренней энергии. Тогда из уравнения (3) следует, что молярная теплоемкость газа при постоянном объеме равна
 . .
| (4) |
2. Изобарический процесс.
Процесс, протекающий при постоянном давлении, называется изобарическим. Для этого случая формула (3) перепишется в виде
 . .
| (5) |
Используя уравнение состояния (2) получаем:
 . .
| (6) |
Но  , следовательно,
, следовательно,  , поэтому
, поэтому  . Подставляя это выражение в уравнение (5) получим
. Подставляя это выражение в уравнение (5) получим
 . .
| (7) |
Сравнивая уравнения (4) и (5) видим, что
 . .
| (8) |
Уравнение (8) называется уравнением Майера.
3. Изотермический процесс.
Изотермическим процессом называется процесс, протекающий при постоянной температуре. В этом случае  и
и  , то есть внутренняя энергия газа остается постоянной и все подводимое тепло расходуется на работу.
, то есть внутренняя энергия газа остается постоянной и все подводимое тепло расходуется на работу.
4. Адиабатический процесс.
Процесс, протекающий без теплообмена с окружающей средой, называется адиабатическим. В этом случае  . Первое начало термодинамики для такого процесса будет иметь вид:
. Первое начало термодинамики для такого процесса будет иметь вид:

или
 ,
,
то есть при адиабатическом процессе расширения или сжатия, работа совершается газом только за счет изменения запаса внутренней энергии.
Выведем уравнение адиабатического процесса. При адиабатическом расширении работа совершается за счет убыли внутренней энергии  . Так как
. Так как  и
и 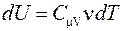 , то
, то
 .
.
Разделив уравнение (6) на  и учитывая последнее уравнение и (8), получим
и учитывая последнее уравнение и (8), получим
 ,
,
откуда
 ,
,
где  – показатель адиабаты.
– показатель адиабаты.
Интегрируя и потенцируя последнее уравнение, получим уравнение Пуассона
 . .
| (9) |
Согласно кинетической теории газов из (4) и (7), получим
 .
.
Эта формула справедлива как для молярных, так и для удельных теплоемкостей газов.