Описание установки и метода измерений.

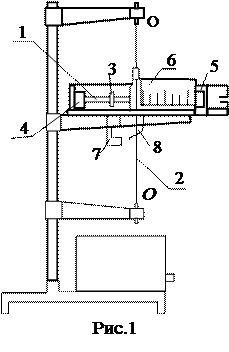
В настоящей работе роль баллистического маятника играет стержень 1, подвешенный на натянутой стальной проволоке 2 (рис.1). На этом стержне имеются два груза 3, которые могут передвигаться, и две чашечки 4, заполненные пластилином. Маятник может вращаться вокруг вертикальной оси ОО', совпадающей с проволокой. "Пуля", вылетающая из пружинной "пушки" 5, попадает в чашечку с пластилином и застревает в ней. В результате указанного воздействия маятник приходит в колебательное движение.

При отклонении маятника от положения равновесия на угол jв проволоке подвеса возникает упругий возвращающий момент силы M, который по закону Гука пропорционален этому углу: M = -kj, (1)

где k - коэффициент упругости стальной проволоки.

Как известно, основной закон динамики вращательного движения имеет вид M = Jb, (2)

где J- момент инерции маятника, b = d²j ¤ dt² - угловое ускорение.

Тогда уравнение (2) примет вид:

d²j ¤ dt² + kj ¤ J = 0 (3)

Дифференциальное уравнение такого вида описывает гармонические колебания и его решением является функция

j = j₀.sin wt = j₀.sin 2pt ¤ T, (4)

где j₀.- максимальный угол отклонения маятника (амплитуда),

w - циклическая частота колебаний, T - период колебаний маятника.

Для гармонических колебаний: (5)

Соотношения (3-5) записаны при условии пренебрежимо малого затухания колебаний.

Для нахождения выражения, определяющего скорость полета "пули" V, воспользуемся законом сохранения момента импульса. Поскольку до соударения маятник покоится, момент импульса системы "пуля" - маятник (относительно оси вращения маятника) равен моменту импульса "пули" относительно этой оси L = mVr (6)

Где m – масса "пули", r - расстояние от линии полета "пули" до оси вращения маятника.

После неупругого удара момент импульса системы: L₂.= Jw₀, (7)

где w₀. - максимальная угловая скорость, приобретаемая маятником в результате удара. Согласно (4), угловая скорость колебаний маятника в произвольный момент времени

w = dj ¤ dt =j₀ 2p ¤ T* cos 2pt ¤ T = w₀ cos 2pt ¤ T (8)

Таким образом, амплитудное значение угловой скорости w₀ = j₀ 2p ¤ T

определяется максимальным углом отклонения маятника j₀, периодом его колебаний T. По закону сохранения момента импульса mVr= Iw₀ (9)

Откуда V=Jw₀ ¤ mr=2pJj₀ ¤ mr T (10)

В формулу (10) входит неизвеcтный момент инерции маятника.

Его можно определить, пользуясь теоремой Штейнера для двух разных положений грузов относительно оси вращения маятника и соотношением (5). При симметричном положении двух одинаковых грузов относительно оси вращения момент инерции каждого из них равен

J = J₀+ 2m₀.R², (11)

где m₀ - масса каждого груза, R - расстояние каждого груза от оси вращения, J₀- момент инерции маятника при расположении грузов относительно оси вращения (R=0)

При расположении грузов на другом расстоянии R₁ от оси вращения момент инерции маятника равен J₁=J₀+2m₀R₁² (12)

Тогда J₁ –J =2m₀ (R₁²- R²) (13)

Из формул (5) и (13) получим: J= 2m₀ T² (R₁²- R²) ¤ (T₁²- T²) (14)

Подставляя (14) в (10), находим окончательное выражение для вычисления скорости полета "пули": V=4pm₀j₀T(R₁²- R²) ¤ mr (T₁²- T²) (15)

Максимальный угол отклонения j. определяется по круговой шкале 6. Для определения периода колебания T установка снабжена фотоэлектрическим датчиком 7 и электронным секундомером.

Когда указатель 8 пересекает световой луч датчика, специальная электронная схема считывает число колебаний n, одновременнно ведется счет времени t. Значения n, t высвечиваются на табло счетчика колебаний и секундомера. По этим данным рассчитывается период колебаний T= n / t

Выполнение работы.

1. Для "пули", используемой в работе, на технических весах определить ее массу m (погрешность взвешивания составляет ∆m=+0.01г).

2. После включения установки в сеть нажать на клавишу "Сеть", при этом на двух табло электронного блока должны высвечиваться нули.

3. Расположить первоначально грузы 3 симметрично на расстоянии R=(1-3) см от оси вращения. Это расстояние определяется по концентрическим линиям на стержне, причем ∆R=+0.01см. Масса каждого груза равна m.=(200+0.01)г. Отсчетная черта на левой чашке 4 маятника должна совпадать с нулевым делением шкалы (если точного совпадения добиться нельзя, то в последующие отсчеты угла отклонения маятника должна быть внесена соответствующая поправка)

4. Зарядить пружинную "пушку" (первый раз с помощью преподавателя или лаборанта). После выстрела отсчитать максимальный угол j.отклонения маятника.

5. Определить период колебаний маятника T для расстояния R грузов от оси вращения. Для этого нажимается клавиша "СБРОС" после того, как маятник совершит примерно 10 колебаний, нажимается клавиша "СТОП" с индикаторов считываются значения n, t.

6. Расположить грузы на большем расстояния R*от оси вращения, нажать на клавишу "СБРОС", чтобы на табло опять высвечивались лучи, и провести измерения, как указанно в пункте 5., для определения периода колебаний T*.

7. По формуле (15) вычислить скорость полета "пули" V. Расстояние от линии полета "пули" до оси вращения маятника r=(12+0.1)см Все измерения необходимо провести не менее трех раз, и результаты занести в таблицу 1.

8. По результатам эксперимента следует оценить абсолютную и относительную погрешности определения скорости полета "пули" V.,

№.п.п

mкг

R,м

j₀

∆φ₀

t, c

T,c

∆T,c

R_1,m

n₁

t_1,c

T_1,c

∆T₁,c

V, m/c

∆V,m/c

∆v/v* 100%

Ср

Контрольные вопросы.

1. Какие столкновения называются упругими и неупругими?

2. Сформулируйте законы сохранения импульса и момента импульса системы.

3. Запишите уравнение движения для баллистического маятника.

4. Объясните, как при движении крутильного маятника проявляется действие основного закона динамики вращательного движения?

5. Сформулируйте и запишите теорему Штейнера.

РАБОТА № 7

⇐ Предыдущая 13 14 15 16 171819 20 21 22 Следующая ⇒