Описание установки и метода измерений

Машина Атвуда представляет собой стойку 1, в верхней части которой на ось 2 насажен легкий блок 3. Исследуемая механическая система – это два тела 4 одинаковой массы m , подвешенные к концам нити, переброшенной через блок. На правое тело устанавливается небольшой дополнительный грузик 5 массы m₁, под действием которого система начинает двигаться равноускоренно с ускорением а. Ускорение связано со скоростью, приобретаемой на пути S (расстояние между верхним 6 и средним 7 кронштейнами), соотношением (5). Для измерения пути на стойке имеется миллиметровая шкала 8.

Определение скорости производится следующим образом. На среднем 7 и нижнем 9 кронштейнах установки расположены фотоэлектрические датчики. При пересечении светового луча движущимся телом сигнал первого датчика включает электронный секундомер, а сигнал второго датчика выключает его. На индикаторе секундомера 10 высвечивается время t прохождения системой пути S₁ - расстояния между средним и нижним кронштейнами. Средний кронштейн имеет кольцо 11, которое снимает дополнительный грузик . Поэтому на участке пути S₁ система движется равномерно с той скоростью v , которую она приобрела при ускоренном движении: (9)

Из формул (5) и (9) ускорение системы на первом участке пути S можно выразить через величины, которые измеряются в работе:

(10)

Согласно соотношению(8), полученному на основании второго закона Ньютона, ускорение пропорционально действующей на систему силе F=m₁g, т.е. силе тяжести дополнительного грузика. Поэтому, измерив ускорение а при различных значениях m₁, можно проверить справедливость второго закона Ньютона F=(2m+m₁)а и сравнить ускорение, найденное в работе с помощью соотношения (10), с теоретическим значением, рассчитанным по формуле (8). Трением в блоке, его инертностью и сопротивлением воздуха при этом пренебрегают.

Выполнение работы

1. Имеющимися внизу регулируемыми ножками выровняйте прибор так, чтобы правое тело свободно проходило через крыльцо. Включите сетевой шнур в сеть 220 В . Нажмите кнопку «СЕТЬ» . При этом загораются лампочки фотоэлектрических датчиков и индикатор измерителя времени показывает цифры нуль. Прибор готов к работе.

2. При утопленной кнопке «ПУСК» переместите правое тело в верхнее положение так, чтобы нижняя грань этого тела совместилась с чертой на верхнем кронштейне. Отожмите кнопку «ПУСК» и система будет удерживаться в исходном положении электромагнитным тормозом.

3. Поместите на правое тело один из дополнительных грузиков. Нажмите кнопку «ПУСК» , при этом система приходит в движение. После прекращения движения с индикатора считывается время t. Нажмите кнопку «СБРОС» и проделайте данное упражнение с другим дополнительным грузиком. Значения S и m₁, при которых проводятся измерения, указываются преподавателем. Измерения с каждым из дополнительных грузиков проводятся не менее пяти раз, на основании чего определяется среднее значение t_ср для каждого грузика (масса m₁ указана на грузиках.

Результаты измерений оформляются в виде таблицы.

S,см

S₁,см

m₁,г

t,с

t_ср,c

v,см/с

а,см/c²

а_теор,см/c²

4. Постройте графическую зависимость ускорения а системы от действующей на нее силы m₁g.

5. На основании найденного в эксперименте значения а и известных масс m и m₁ определите из соотношения (8) ускорение свободного падения g.

6. При данной величине массы дополнительного груза m₁ постройте зависимость V² от S. Масса каждого тела m = 60,6 г.

Контрольные вопросы

1. Выведите формулы (5) и (8) из законов кинематики и динамики равноускоренного движения.

2. При каких упрощающих предположениях проводится проверка законов кинематики и динамики на машине Атвуда?

3. Объяснить , как при движении системы тел на машине Атвуда проявляется действие всех трех законов Ньютона.

4. Под действием какой силы тела на машине Атвуда движутся ускоренно? Почему их ускорение меньше ускорения свободного падения?

5. Как на машине Атвуда измеряется мгновенная скорость ускоренно движущегося тела?

5. КИНЕМАТИКА И ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ

1. Угловая скорость и угловое ускорение. Любое твердое тело можно рассматривать как систему материальных точек, причем масса 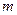тела равна сумме масс этих точек: (1)

Каждая из этих материальных точек при вращении тела имеет траекторию движения в виде окружности, центр которой лежит на оси вращения. Очевидно, что линейная скорость каждой -той точки зависит от расстояния до оси вращения и поэтому она не может служить кинематической характеристикой вращательного движения твердого тела. Равномерное движение материальной точки по окружности можно характеризовать угловой скоростью. Под угловой скоростью понимается векторная величина , численное значение которой равно отношению угла поворота 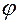к промежутку времени , за который этот поворот

произошел: (2).

Для неравномерного вращательного движения вводится понятие мгновенной угловой скорости: (3).

Единицей измерения угловой скорости является радиан в секунду (рад/с) или с^-1.

Вектор угловой скорости направлен вдоль оси вращения тела таким образом, чтобы его направление совпадало с направлением поступательного движения правовинтового буравчика, ось которого расположена вдоль оси вращения тела , а головка вращается вместе с телом (рис. 1). Из этого рисунка видно, что все три вектора , и взаимно перпендикулярны, поэтому зависимость между линейной и угловой скоростями можно записать в виде векторного произведения: (4)

Для характеристики неравномерного вращения тела вводится понятие вектора углового ускорения . Вектор углового ускорения в каждый момент времени равен скорости изменения вектора угловой скорости:

(5)

Единицей измерения углового ускорения является радиан на секунду в квадрате (рад/с²) или с^-2. На рис. 2 показаны два возможных направления вектора углового ускорения.

Если вращение тела вокруг неподвижной оси происходит ускоренно, то вектор углового ускорения совпадает по направлению с вектором угловой скорости (рис. 2а). В случае замедленного вращения вектора и направлены противоположно друг другу (рис. 2б).

2. Момент силы и момент инерции

Возьмем некоторое тело, которое может вращаться вокруг неподвижной оси (рис. 3).

Для того чтобы привести тело во вращательное движение, пригодна не всякая внешняя сила. Эта сила должна обладать вращающим моментом относительно данной оси, а направление силы не должно быть параллельным данной оси или пересекаться с ней. Подействуем на тело силой . Вращение тела будет определяться моментом силы относительно оси вращения: , (6)

где - радиус- вектор, проведенный из центра окружности вращения в точку приложения силы . Из векторного произведения (6) следует, что вектор момента силы направлен перпендикулярно плоскости, в которой лежат векторы и , т.е. в соответствии с правилом буравчика. Численное значение момента силы определяется выражением: , (7)

где 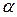- угол между векторами и . Как видно из рис. 3, величина , равная расстоянию от оси вращения до направления действия силы , называется плечом силы относительно этой оси. Следовательно, момент силы численно равен произведению силы на плечо:

M = F·h (8).

Таким образом, физический смысл момента силы состоит в том, что при вращательном движении воздействие силы определяется не только величиной силы, но и тем, как она приложена.

В динамике вращательного движения вводится понятие момента инерции. Представим твердое тело, которое может вращаться вокруг неподвижной оси , как систему материальных точек m_i (рис. 4).Очевидно, что каждая точка m_i будет находиться на определенном расстоянии r_i до оси вращения.

Величина , численно равная произведению массы точки m_i на квадрат ее расстояния до оси вращения, называется моментом инерции точки относительно оси вращения. Моментом инерции тела называется сумма моментов инерции всех материальных точек, составляющих тело, т.е.: (9).

Физический смысл момента инерции J состоит в том, что при вращательном движении инерция тела определяется не только величиной массы, но и распределением этой массы относительно неподвижной оси вращения.

На рис. 5 приведены формулы моментов инерции некоторых тел правильной геометрической формы относительно оси, проходящей через центр тяжести (ось симметрии).

3. Основной закон динамики вращательного движения имеет вид:

, (10)

т.е. угловое ускорение прямо пропорционально моменту силы, действующей на тело и обратно пропорционально моменту инерции тела. Этот закон аналогичен основному закону динамики для поступательного движения (второму закону Ньютона): .При вращении тела аналогично понятию импульса тела для поступательного движения ( ) вводят понятие момента импульса тела , который равен (11).

4. Аналогично закону сохранения импульса для поступательного движения при вращательном движении действует закон сохранения момента импульса: , (12),

где и - моменты инерции и угловые скорости тел, составляющих изолированную систему. Он гласит:

в изолированной системе (т.е. момент внешних сил ) сумма моментов импульса всех тел есть величина постоянная.

Для изолированной системы, состоящей из одного вращающегося тела, закон сохранения (12) запишется в виде: (13).

5. Как известно, кинетическая энергия поступательно движущегося тела определяется уравнением . Аналогично этому выражению кинетическая энергия тела, вращающегося вокруг неподвижной оси, определяется уравнением: (14).

РАБОТА № 5-1

ОПРЕДЕЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ ТВЕРДЫХ ТЕЛ

⇐ Предыдущая 8 9 10 11 121314 15 16 17 Следующая ⇒