 |
|
Перечень программных вопросов по пройденному курсу и соответствующих
итоговым тестам:
1. Матрицы. Виды матриц.
2. Операции над матрицами (умножение матрицы на число, сложение, вычитание, умножение, транспонирование). Свойства операций над матрицами.
3. Определители второго и третьего порядков.
4. Миноры и алгебраические дополнения. Разложение определителя по элементам строки или столбца.
5. Свойства определителей.
6. Определители n-го порядка.
7. Обратная матрица. Невырожденная матрица. Алгоритм нахождения обратной матрицы.
8. Ранг матрицы. Элементарные преобразования матрицы. Алгоритм вычисления ранга матрицы.
9. Системы линейных уравнений (совместная, несовместная, определенная, неопределенная, однородная, неоднородная).
10. Система n линейных уравнений с n переменными. Правило Крамера и матричный методрешения систем линейных уравнений.
11. Система m линейных уравнений с n переменными.Исследование системы уравнений. Теорема Кронекера-Капелли.
12. Метод Гаусса.
13. Система линейных однородных уравнений. Фундаментальная система решений.
14. Векторы на плоскости и в пространстве. Нулевой вектор, равные, коллинеарные, компланарные векторы. Линейные операции над векторами (сложение, умножение на число). Проекция вектора на ось.
15. Прямоугольная система координат.Разложение вектора по ортам.Координаты вектора.Длина вектора. Направляющие косинусы вектора.
16. Действия над векторами, заданными проекциями. Условия равенства и коллинеарности векторов.
17. Скалярное произведение векторови его свойства.
18. Выражение скалярного произведения через координаты.
19. Угол между двумя векторами. Условие перпендикулярности векторов. Проекция вектора на заданное направление.
20. Понятия n-мерного вектора и векторного пространства.
21. Линейная зависимость и независимость векторов. Размерность и базис векторного пространства.
22. Простейшие задачи аналитической геометрии: расстояние между двумяточками, деление отрезка в данном отношении.
23. Уравнение линии на плоскости. Уравнение прямой, проходящей через данную точку перпендикулярно данному вектору. Общее уравнение прямой. Уравнение прямой с угловым коэффициентом. Каноническое уравнение прямой. Параметрические уравнения прямой. Уравнение прямой, проходящей через две данные точки.
24. Угол между двумя прямыми. Условия параллельности и перпендикулярности прямых. Расстояние от точки до прямой.
25. Уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору. Общее уравнение плоскости. Уравнение плоскости в отрезках. Расстояние от точки до плоскости.
26. Угол между двумя плоскостями. Условия параллельности и перпендикулярности плоскостей.
27. Прямая в пространстве. Канонические уравнения прямой. Параметрические уравнения прямой. Уравнение прямой, проходящей через две данные точки.
28. Угол между двумя прямыми в пространстве. Условия параллельности и перпендикулярности прямых.
29. Прямая и плоскость в пространстве. Угол между прямойи плоскостью. Условия параллельности и перпендикулярности прямой и плоскости.
30. Понятие функции. Область определения и область значений функции.
31. Основные свойства функций.
32. Основные элементарные функции.
33. Числовая последовательность и ёё предел.
34. Бесконечно большая функция.
35. Бесконечно малые функции и их свойства. Связь между бесконечно большими и бесконечно малыми функциями.
36. Основные теоремы о пределах.
37. Раскрытие неопределенностей.
38. Первый и второй замечательные пределы.
39. Сравнение бесконечно малых. Эквивалентные бесконечно малые, их использование при вычислении пределов.
40. Непрерывность функции. Непрерывность основных элементарных функций.
41. Точки разрыва функции и их классификация.
42. Свойства функций, непрерывных на отрезке.
43. Определение производной функции, ее геометрический и механический смысл.
44. Правила дифференцирования.
45. Производная сложной функции.
46. Производные основных элементарных функций.
47. Таблица производных.
48. Дифференциал функции.
49. Производные высших порядков.
50. Экономический смысл производной.
51. Раскрытие неопределенностей. Правило Лопиталя.
52. Условия возрастания и убывания функции.
53. Экстремум функции. Необходимые и достаточные условия экстремума.
54. Наибольшее и наименьшее значения функции на отрезке.
55. Выпуклость функции. Точки перегиба.
56. Асимптоты кривых: вертикальные, горизонтальные, наклонные.
57. Область определения функции двух переменных.
58. Линии и поверхности уровня.
59. Частные приращения и частные производные функции нескольких переменных.
60. Полное приращение и полный дифференциал функции.
61. Дифференцирование неявной функции.
62. Производная по направлению.
63. Градиент.
64. Частные производные и полные дифференциалы высших порядков.
65. Экстремумы функции двух переменных. Необходимые и достаточные условия экстремума.
66. Первообразная. Неопределенный интеграл.
67. Свойства неопределенного интеграла.
68. Таблица основных интегралов.
69. Метод непосредственного интегрирования.
70. Метод интегрирования подстановкой (замена переменной).
71. Метод интегрирования по частям.
72. Определение определенного интеграла, его геометрический и экономический смысл.
73. Свойства определенного интеграла.
74. Формула Ньютона – Лейбница.
75. Замена переменной в определенном интеграле.
76. Интегрирование по частям в определенном интеграле.
77. Вычисление площадей плоских фигур.
78. Вычисление длины дуги плоской кривой.
79. Вычисление объема тела вращения.
80. Вычисление площади поверхности вращения.
81. Несобственные интегралы с бесконечными пределами интегрирования.
82. Несобственные интегралы от разрывных функций.
83. Понятие дифференциального уравнения. Порядок и решение дифференциального уравнения.
84. Уравнения с разделяющимися переменными.
85. Однородные дифференциальные уравнения первого порядка.
86. Линейные дифференциальные уравнения первого порядка.
87. Числовые ряды.Сходимость и сумма ряда.
88. Необходимый признак сходимости числового ряда.
89. Достаточные признаки сходимости рядов с положительными членами.
90. Знакочередующиеся ряды. Признак Лейбница.
91. Знакопеременные ряды. Абсолютная и условная сходимости.
92. Степенные ряды. Теорема Абеля. Интервал и радиус сходимости степенного ряда.
93. Ряды Тейлораи Маклорена.Разложение функций в степенные ряды.
Глоссарий
1. Матрицейразмера m  называется прямоугольная таблицачисел,
называется прямоугольная таблицачисел,
состоящая из m строк и n столбцов.
2. Квадратной называется матрица, у которой число строк равно числу столбцов.
3. Порядком квадратной матрицы называется число ёё строк (столбцов).
4. Диагональной называется квадратная матрица, у которой вне главной диагонали стоят нулевые элементы.
5. Единичной матрицей, называется диагональная матрица, у которой элементы, стоящие на главной диагонали равны единице.
6. Треугольной матрицей называется квадратная матрица, все элементы которой, стоящие выше или ниже главной диагонали, равны нулю.
7. Транспонирование матрицы– переход от матрицыА к матрице  , в которой каждая ее строка заменена столбцом с тем же номером.
, в которой каждая ее строка заменена столбцом с тем же номером.
8. Ступенчатой матрицей называется матрица вида:

где  i = 1,2, …, r; r
i = 1,2, …, r; r 
9. Суммой матриц А =  и
и  одинакового размера называется матрица
одинакового размера называется матрица
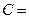 A + B, каждый элемент которой равен сумме соответствующих элементов матриц А и В, т. е.
A + B, каждый элемент которой равен сумме соответствующих элементов матриц А и В, т. е.  .
.
10. Произведением матрицы 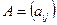 на число
на число 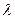 называется матрица C =lA, каждый элемент
называется матрица C =lA, каждый элемент 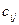 которой равен
которой равен  , т.е.
, т.е.  .
.
11. Произведением матрицы 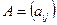 размера
размера  на матрицу
на матрицу  размера
размера  называется матрица
называется матрица 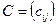 размера
размера  , каждый элемент
, каждый элемент 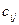 которой равен произведению i-той cтроки матрицы А на j -тый столбец матрицы В,т.е.
которой равен произведению i-той cтроки матрицы А на j -тый столбец матрицы В,т.е.
 ;
;  1, 2, …, m; j =1, 2, …, k.
1, 2, …, m; j =1, 2, …, k.
12. Определителем матрицы второго порядканазывается число, обозначаемое символом  и определяемое равенством:
и определяемое равенством:
 .
. 
13. Определителем матрицы третьего порядка называется число, определяемое равенством:
 =
=  = а11а22а33 + а12а23а31 + а13а21а32 – а13а22а31 – а12а21а33 – а11а23а32 .
= а11а22а33 + а12а23а31 + а13а21а32 – а13а22а31 – а12а21а33 – а11а23а32 .
14. Минором элемента aij квадратной матрицы A порядка n называется определитель матрицы порядка n –1, полученный из матрицы A вычеркиванием i-й строки и j -го столбца. Обозначается Mij.
15. Алгебраическим дополнением элемента aij квадратной матрицы A называется величина
Aij = (–1)i+j Mij.
16. Обратной матрицей для квадратной матрицы А называется такая матрица  , что выполняется равенство
, что выполняется равенство
A 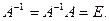
17. Невырожденной называется квадратная матрица, определитель которой не равен нулю.
18. Вырожденной называется квадратная матрица, определитель которой равен нулю
19. Присоединённой матрицейдля квадратной матрицы А называется матрица 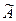 , элементами которой являются алгебраические дополнения транспонированной матрицы А.
, элементами которой являются алгебраические дополнения транспонированной матрицы А.
20. Минором k -го порядкаматрицы А называется определитель матрицы k-го порядка, составленной из элементов, стоящих на пересечении k строк и k столбцов матрицы A.
21. Рангомматрицы А называетсянаивысший порядок отличных от нуля миноров этой матрицы (обозначается r (A)).
22. Системой из m линейных алгебраическихуравнений c n неизвестныминазывается система вида:
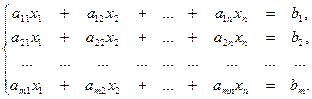
23. Решением системы называется упорядоченный набор чисел (  ), который после подстановки в систему превращает все ёё уравнения в тождества.
), который после подстановки в систему превращает все ёё уравнения в тождества.
24. Cовместной называетсясистема, имеющая решение.
25. Несовместной называетсясистема, не имеющая решение.
26. Матрицей системы называется матрица А,составленная из коэффициентов при неизвестных данной системы.
27. Расширеннойматрицей системы называется матрица  , получаемая изматрицысистемы добавлением справа столбца свободных членов системы.
, получаемая изматрицысистемы добавлением справа столбца свободных членов системы.
28. Формулами Крамера называются формулы
xi=  , i = 1, 2,…, n,
, i = 1, 2,…, n,
где – определитель матрицысистемы,
– определитель матрицысистемы, 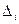 – определитель, получаемый из матрицысистемызаменой i -того столбца на столбец свободных членов.
– определитель, получаемый из матрицысистемызаменой i -того столбца на столбец свободных членов.
29. Исследовать систему – значит определить, совместна ли она и, в случае совместности, определить, сколько решений она имеет.
30. Эквивалентными системами линейных уравнений относительно одного и того же числа неизвестныхназываются системы, имеющие одинаковые решения.
31. Базисным минором называется любой изотличный от нуля миноров матрицысистемы, порядок которого равен рангу r (A).
32. Базисными неизвестными называются неизвестные, коэффициенты которых входят в базисный минор,
33. Однородной системой линейных уравнений называется система все свободные члены которой равны нулю.
34. Вектором называется направленный отрезок.
35. Коллинеарными называются векторы, лежащие на одной или на параллельных прямых.
36. Равныминазываются векторы, если они коллинеарны, одинаково направлены и равны по модулю.
37. Компланарными называются вектора, лежащие либо в одной плоскости, либо в параллельных плоскостях.
38. Суммой 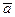 +
+  двух векторов
двух векторов 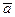 и
и  называется вектор, начало которого совпадает с началом вектора
называется вектор, начало которого совпадает с началом вектора 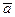 , а конец – с концом вектора
, а конец – с концом вектора  :
:

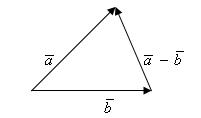
39. Разностью 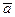 –
–  векторов
векторов 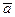 и
и  , выходящих из одной точки, называется вектор, соединяющий конец вектора
, выходящих из одной точки, называется вектор, соединяющий конец вектора  с концом вектора
с концом вектора 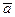 :
:
40. Произведением вектора 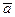 на число
на число 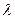 называется вектор
называется вектор 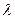
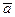 , удовлетворяющий трем условиям:
, удовлетворяющий трем условиям:
1) | 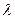
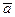 | =|
| =|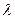 ||
|| 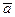 |,
|, 
2) 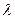
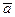 | |
| | 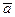 ,
,
3) вектор 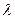
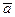 одинаково направлен с вектором
одинаково направлен с вектором 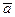 , если
, если 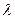 >0 и направлен в противоположную сторону, если
>0 и направлен в противоположную сторону, если 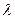 <0.
<0.
41. Проекцией точки А на осьl называется точка пересечения оси l с плоскостью, проходящей через точку А перпендикулярно оси.
42. Разложением вектора  по векторам
по векторам  называется равенство
называется равенство
 =
=  .
.
43. Линейной комбинацией векторов  с коэффициентами
с коэффициентами 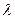 1,
1, 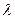 2,…,
2,…, 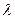 n называется выражение
n называется выражение  .
.
44.Вектора  называются линейно зависимыми, если найдутся такие числа,
называются линейно зависимыми, если найдутся такие числа,  ,
,  ,…,
,…,  , из которых хотя бы одно отлично от нуля, что линейная комбинация векторов
, из которых хотя бы одно отлично от нуля, что линейная комбинация векторов  с указанными числами обращается в нуль, т.е. имеет место равенство
с указанными числами обращается в нуль, т.е. имеет место равенство

 = 0.
= 0.
45.Вектора  называются линейно независимыми, если их линейная комбинация
называются линейно независимыми, если их линейная комбинация  равна нулю только в случае, когда все коэффициенты
равна нулю только в случае, когда все коэффициенты 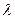 1,
1, 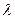 2,…,
2,…, 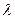 n равны нулю.
n равны нулю.
46. Базисным вектором прямой называется любой ненулевой вектор  этойпрямой.
этойпрямой.
47. Базисом плоскости называется любая пара неколлинеарных векторов {  ,
,  } этой плоскости.
} этой плоскости.
48. Базисом пространства называется любая тройка некомпланарных векторов {  ,
,  ,
, 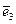 } этого пространства.
} этого пространства.
49. Координатами вектора 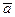 в данном базисеназываются коэффициенты линейной комбинации базисных векторов, выражающих вектор
в данном базисеназываются коэффициенты линейной комбинации базисных векторов, выражающих вектор 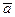 на прямой, в плоскости или в пространстве.
на прямой, в плоскости или в пространстве.
50. Размерностью пространства (плоскости, прямой) называется число векторов в базисе.
51. Формулой разложения вектора в пространстве по ортонормированному базисуназывается формула вида
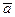 = x
= x  + y
+ y  + z
+ z  .
.
52. Скалярным произведением двух векторов 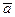 и
и  называется число, равное произведению длин этих векторов на косинус угла между ними:
называется число, равное произведению длин этих векторов на косинус угла между ними:
 =|
=| 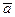 ||
||  | cos (
| cos (  ).
).
53. Уравнением прямой, проходящей через данную точкуM0(x0, y0) перпендикулярно данному нормальному вектору  называетсяуравнение вида
называетсяуравнение вида
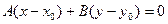 .
.
54. Общим уравнением прямойназываетсяуравнение вида
Ax + By + C = 0.
55. Уравнением прямой в “отрезках” называется уравнение вида
 .
.
56. Направляющим вектором прямой называется любой ненулевой вектор, коллинеарный данной прямой.
57. Параметрическими уравнениями прямойL снаправляющим вектором  и точкой М0
и точкой М0  называются уравнения вида
называются уравнения вида
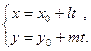
58. Каноническим уравнением прямой называется уравнение вида
 .
.
59. Уравнение прямой, проходящей через две точки M1(x1; y1) и M2(x2; y2) имеет вид
 .
.
60. Уравнением прямой с угловым коэффициентом называется уравнение вида  .
.
61. Уравнением прямой, проходящей через данную точку M0(x0, y0)с данным угловым коэффициентом называется уравнение вида
 .
.
62. Уравнением плоскости, проходящей через точку M0(x0,y0,z0) перпендикулярно вектору  называется уравнение вида
называется уравнение вида
 .
.
63. Общим уравнением плоскостиназываетсяуравнение вида
Ax + By + Cz + D = 0.
64. Уравнением плоскости в “отрезках”называетсяуравнение вида
 .
.
65. Параметрическими уравнениями прямойL снаправляющим вектором 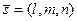 и точкой M0(x0, y0, z0)
и точкой M0(x0, y0, z0)  называются уравнения вида
называются уравнения вида

66. Каноническими уравнениями прямой в пространстве называются уравнения вида
 .
.
67. Уравнения прямой в пространстве, проходящей через две точки M1(x1; y1) и M2(x2; y2) имеют вид
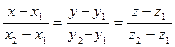 .
.
68. Функцией  с областью определения
с областью определения  иобластью значений
иобластью значений  называется некоторое отображение из
называется некоторое отображение из  в
в 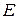 , т. е. соответствие, при котором каждому элементу
, т. е. соответствие, при котором каждому элементу  сопоставляется единственный элемент
сопоставляется единственный элемент  .
.
69. Пределомпоследовательности  называется число а (обозначается
называется число а (обозначается  ), если для любого числа
), если для любого числа  найдётся такое натуральное число N, что при всех
найдётся такое натуральное число N, что при всех  , выполняется неравенство
, выполняется неравенство 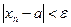 .
.
70. Пределом функции  при
при  называется такое число
называется такое число  (обозначается
(обозначается  ), если для любого
), если для любого  найдётся такое d>0, что для всех
найдётся такое d>0, что для всех  , удовлетворяющих неравенству |
, удовлетворяющих неравенству |  , выполняется неравенство
, выполняется неравенство  .
.
71.Функция  называетсянепрерывнойв точке
называетсянепрерывнойв точке  , если выполняются три условия: 1)
, если выполняются три условия: 1)  ; 2)
; 2)  ; 3)
; 3) 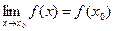 .
.
72. Производной функции в точке
в точке  (обозначается
(обозначается  ) называется предел отношения приращения этой функции к приращению ее аргумента в точке
) называется предел отношения приращения этой функции к приращению ее аргумента в точке  , когда приращение аргумента стремится к нулю.
, когда приращение аргумента стремится к нулю.
73. Дифференциалом функции  в точке
в точке  (обозначается
(обозначается  или
или  ) называется главная, линейная относительно
) называется главная, линейная относительно 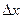 ,часть приращения функции, равная произведению производной функции на приращение аргумента в точке
,часть приращения функции, равная произведению производной функции на приращение аргумента в точке  .
.
74. Асимптотойкривой называется такая прямая, что расстояние от точки на кривой до этой прямой стремится к нулю при удалении точки вдоль кривой в бесконечность.
75. Функция нескольких переменныхu = f(  ,
,  ,…,xn) – это функция, область определения которой принадлежит
,…,xn) – это функция, область определения которой принадлежит  , а область значений принадлежит действительной оси.
, а область значений принадлежит действительной оси.
76. Частной производной по xфункции  в точке М(х, y)называется предел отношения частного приращения по х функции в этой точке к приращению
в точке М(х, y)называется предел отношения частного приращения по х функции в этой точке к приращению 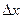 аргумента х при
аргумента х при  .
.
77. Частной производной n–го порядкафункции  называется частная производная от одной из ее производных
называется частная производная от одной из ее производных  порядка.
порядка.
78. окрестностьюточки
окрестностьюточки 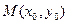 на плоскости (или
на плоскости (или  в пространстве) называется круг радиуса
в пространстве) называется круг радиуса  с центром в точке
с центром в точке  без окружности (или шар без сферы).
без окружности (или шар без сферы).
79. Линией уровня  функции двух переменных
функции двух переменных  называется множество
называется множество
всех точек  из ее области определения, координаты которых удовлетворяют уравнению
из ее области определения, координаты которых удовлетворяют уравнению  .
.
80. Поверхностью уровня 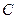 функции
функции  называется множество всех
называется множество всех
точек из области определения этой функции, координаты которых удовлетворяют уравнению 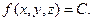
81. Точкой максимума функции двух переменных  называется такая точка М
называется такая точка М  (
(  ,
,  ), если существует окрестность этой точки, что для всех точек
), если существует окрестность этой точки, что для всех точек  из этой окрестности выполняется неравенство
из этой окрестности выполняется неравенство 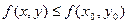 .
.
82. Точкой минимумафункции двух переменных  называется такая точка М
называется такая точка М  (
(  ,
,  ), если существует окрестность этой точки, что для всех точек
), если существует окрестность этой точки, что для всех точек  из этой окрестности выполняется неравенство
из этой окрестности выполняется неравенство  .
.
83. Экстремальная точка функции – это точка максимума или минимума этой функции.
84. Первообразнойдля функции  определенной в интервале
определенной в интервале 
называется такая функция  , производная которой совпадает с
, производная которой совпадает с  в интервале
в интервале  , т.е.
, т.е. 
 .
.
85. Неопределенным интеграломфункции  называется множество всех ее
называется множество всех ее
первообразных на интервале  иобозначается символами
иобозначается символами  , где
, где 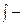 знак интеграла,
знак интеграла,  - дифференциал переменной x. Если
- дифференциал переменной x. Если  какая либо первообразная функции
какая либо первообразная функции  , то
, то  ,
,  .
.
86. Интегральной суммой для функции  , построенной по разбиению
, построенной по разбиению 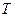 отрезка
отрезка  , называется сумма произведений значений функции в выбранных точках
, называется сумма произведений значений функции в выбранных точках  на длины элементарных участков и обозначается:
на длины элементарных участков и обозначается:
 .
.
87. Определенным интегралом от функции  на отрезке
на отрезке  называется
называется
предел интегральных сумм этой функции по разбиениям  , у которых максимальный
, у которых максимальный  стремится к нулю.
стремится к нулю.
88. Несобственным интегралом  от функции f (x) на промежутке [a; + ¥) называется предел:
от функции f (x) на промежутке [a; + ¥) называется предел: 
 .
.
89. Дифференциальным уравнениемназывается уравнение, связывающее независимую переменную x, искомую функцию  и ее производные
и ее производные 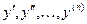 , т.е. уравнение вида
, т.е. уравнение вида  , где
, где  - некоторая функция
- некоторая функция  переменных.
переменных.
90. Порядком дифференциального уравнения называется порядок наивысшей производной, явно входящей в это уравнение
91. Решениемдифференциального уравнения называется функция  , которая при подстановке в дифференциальное уравнение обращает его в тождество.
, которая при подстановке в дифференциальное уравнение обращает его в тождество.
92. Интегрированием дифференциальногоуравнения называется процесс отыскания решений дифференциального уравнения.
93.Интегральной кривой называется график решения дифференциального уравнения.
94. Начальным условием для дифференциального уравнения первого порядка называется такое условие, что при  решение этого уравнения
решение этого уравнения  должно быть равно заданному числу
должно быть равно заданному числу  : (
: (  или
или  ).
).
95. Задачей Коши называется задача отыскания решения уравнения, удовлетворяющего заданному начальному условию.
96. Общим решениемдифференциального уравнения первого порядка называется функция y = y(x, C), удовлетворяющая следующим условиям: 1) она является решением дифференциального уравнения при любом конкретном значении постоянной 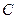 ; 2) для любых начальных условий
; 2) для любых начальных условий  , где
, где  можно найти такое значение
можно найти такое значение  , что функция y = y(x, C0) удовлетворяет данному начальному условию.
, что функция y = y(x, C0) удовлетворяет данному начальному условию.
97. Общим интегралом дифференциального уравнения первого порядка называется равенство вида  , неявно задающее его общее решение.
, неявно задающее его общее решение.
98. Частным решением (интегралом) дифференциального уравнения первого порядка называется решение, полученное из общего решения (интеграла) этого дифференциального уравнения при фиксированном значении С.
99. Уравнением с разделяющимися переменными называется дифференциальное уравнение вида  .
.
100. Однородной функцией  называется функция, для которой при любом
называется функция, для которой при любом  и любых х и у из области определения функции, справедливо тождество
и любых х и у из области определения функции, справедливо тождество 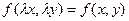 .
.
101. Однородным дифференциальным уравнениемпервого порядка называется уравнение вида 
 , если функция
, если функция  есть однородная функция нулевого измерения относительно x и
есть однородная функция нулевого измерения относительно x и 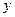 .
.
102. Линейным дифференциальным уравнением первого порядканазывается уравнение вида  .
.
103.Числовым рядомназывается выражение вида
 =
=  .
.
104. Частичной суммой ряда называется сумма первых n членов этого ряда.
105. Суммой ряданазывается конечный предел частичных сумм этого ряда при 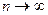 ,
,  .
.
106. Сходящимсяназывается ряд, имеющий сумму:  .
.
107. Расходящимся называется ряд, предел частичных сумм которого не существует (например, равен  ).
).
108. Знакочередующимся рядомназывается числовой ряд вида
 =
=  ,
,
где  для
для  .
.
109. n - ым остаткомсходящегося ряда называется разность между его суммой  и частичной суммой
и частичной суммой  :
:  .
.
110. Абсолютно сходящимсярядом называется знакопеременный ряд, если ряд, составленный из абсолютных величин членов ряда, сходится.
111. Условно сходящимсярядом называется сходящийся знакопеременный ряд,если ряд, составленный из абсолютных величин членов ряда, расходится.
112. Функциональнымрядомназывается выражение вида
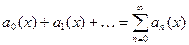 ,
,
где  есть некоторые функции от х.
есть некоторые функции от х.
113. Областью сходимостифункционального ряда называется множество всех значений аргумента x, при которых этот ряд сходится.
114.Степенным рядомназываетсяфункциональный ряд вида  .
.
115. Радиусом сходимостистепенного ряда  называется наибольшее значение
называется наибольшее значение  такое, что в интервале
такое, что в интервале  этот ряд сходится.
этот ряд сходится.
116. Многочленом Тейлора n-го порядка для функции  с центром в точке
с центром в точке  называется многочлен:
называется многочлен:

117. Формулой Тейлора с остаточным членом в форме Лагранжа называется соотношение
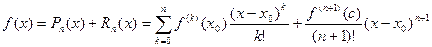 .
.
118. Рядом Тейлорадля функции  с центром в точке
с центром в точке  называется ряд
называется ряд

119. Рядом Маклорена для функции  называется ряд Тейлора с центром в точке
называется ряд Тейлора с центром в точке 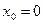
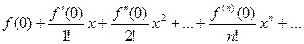 .
.