 |
|
Тема 2 : Достаточные признаки сходимости рядов
С положительными членами
2.1. Признаки сравнения
Пусть даны два ряда с положительными членами:
(1)
(2)
Признак сравнения. Если для всех членов рядов (1) и (2), начиная с некоторого номера, выполняется неравенство 
и ряд (2) сходится, то сходится и ряд (1). Аналогично, если 
и ряд (2) расходится, то расходится и ряд (1).
Пусть 
и 
соответственно частичные суммы рядов (1-2), а Q - сумма ряда (2). Тогда для достаточно больших п имеем
.
Так как 
и ограничена, то 
, т.е. ряд (1) сходится.
Аналогично доказывается и вторая часть признака.
Пример 3. Исследовать на сходимость ряд
.
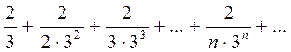Сравним с членами ряда 
.
Начиная с 
, имеем 
.
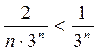Так как ряд 
сходится 
, то данный ряд также сходится.
На практике часто более удобно пользоваться так называемым предельным признаком сравнения, который вытекает из предыдущего.
Предельный признак сравнения. Если для двух рядов (1-2) с положи-тельными членами выполняется условие 
, то
из сходимости ряда (1) следует сходимость ряда (2), а из расходимости ряда (1) следует расходимость ряда (2),т.е. ряды ведут себя одинаково.
Пример 4. Исследовать на сходимость ряд 
.
В качестве ряда для сравнения возьмем гармонический ряд 
,
который является расходящимся.
Тогда
а, следовательно, наш ряд расходится.
Замечание. Часто для сравнения удобно использовать так называемый обобщённый гармонический ряд 
, который, как будет показано ниже, сходится при 
и расходится при 
.
Лекция № 45
2.2. Признак Даламбера
Теорема 1. Пусть для ряда с положительными членами 
сущест-вует конечный или бесконечный предел 
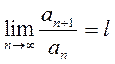, тогда:
1. Если 
- ряд сходится;
2. Если 
- ряд расходится;
3. Если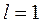 
- ответа на вопрос о сходимости теорема не даёт. В этом случае требуются дополнительные исследования.
Вначале докажем пункт 1. Из определения предела следует: 
выполняется 
или 
. Если , то можно указать такое 
, для которого выполняется 
и тогда 
. Таким образом, 
выполняются равенства:
. (1)
Из формул (1) следует, что ряд 
сходится 
. Тогда по признаку сравнения сходится и ряд .
Аналогично доказывается и случай 2. Здесь имеем 
, и выполняется неравенство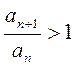 
, т.е. нарушается необходимый признак сходимости, следовательно, ряд расходится.
Пример 1. Исследовать сходимость ряда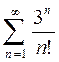 
.
Вычислим предел
Пример 2. Исследовать сходимость ряда 
.
Вычислим предел
т.е. ряд расходится.
2.3. Радикальный признак Коши
Аналогично можно доказать следующую теорему.
Теорема 2. Пусть для ряда с положительными членами сущест-вует конечный или бесконечный предел 
, тогда:
1. Если - ряд сходится;
2. Если - ряд расходится;
3. Если 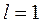- ответа на вопрос о сходимости теорема не даёт. В этом случае требуются дополнительные исследования.
Пример 3. Исследовать сходимость ряда 
.
Вычислим предел
Пример 4. Исследовать сходимость ряда 
.
Вычислим предел
2.4. Интегральный признак Коши
Пусть дан ряд с положительными членами .
Заменим в общем члене ряда 
натуральную переменную п вещественной переменной х. Получим функцию 
, для которой 
. Исходя из геометрического смысла определённого интеграла, можно доказать следующую теорему.
Теорема 3. Если функция непрерывная и невозрастающая на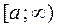 
, тогда:
1. Если интеграл 
сходится, т.е. 
, то ряд сходится;
2. Если интеграл 
расходится, то ряд расходится.
Пример 5. Исследовать на сходимость ряд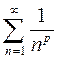 
.
Рассмотрим функцию 
. Для нее имеем
Таким образом, обобщённый гармонический ряд сходится, если и расходится, если . Легко убедиться, что признак Даламбера не даёт ответа на вопрос о сходимости этого ряда.