 |
|
Тема 3 : Знакопеременные ряды
3.1. Знакочередующиеся ряды. Теорема Лейбница
Определение 1. Ряд называется знакопеременным, если среди его членов имеется бесконечное число как положительных, так и отрицательных членов.
Определение 2. Знакопеременный ряд, члены которого имеют чере-дующиеся знаки, называется знакочередующимся рядом.
Такой ряд имеет вид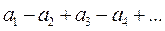 
, где все 
.
Теорема Лейбница. Если в знакочередующемся ряде члены ряда удовлетворяют условиям:
1. 
;
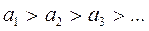2. 
,
то ряд сходится, и его сумма не превосходит первого члена.
Рассмотрим чётные частичные суммы такого ряда
.
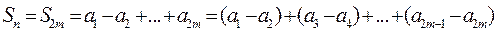Все члены в скобках положительные, следовательно, 
и 
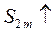с ростом т.
Теперь запишем эту сумму так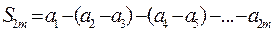 
.
Тогда 
, т.е. сумма ограничена сверху и при этом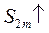 
. Тогда по свойству предела она имеет предел 
, причем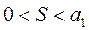 
.
Покажем теперь, что и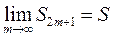 
. Так как 
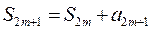, то переходя к пределу в этом равенстве получим
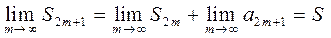, ч.т.д.
Замечание 1. Ошибка, совершаемая при замене S на 
не превосходит по абсолютной величине первого из отброшенных членов, т.е. 
, так как отброшенные члены также образуют знакочередующийся ряд.
Пример 6. Ряд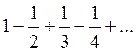 
сходится, так как удовлетворяет усло-виям теоремы Лейбница. При этом приближённое вычисление его суммы будет вычисляться с точностью 
.
Пример 7. Исследовать сходимость ряда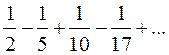 
.
Замечаем, что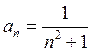 
и тогда по теореме Лейбница
1. 
; 2.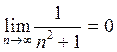 
, т.е. ряд сходится.
3.2. Абсолютная и условная сходимость
Теорема. Если ряд, составленный из абсолютных величин членов данного ряда, сходится, то сходится и данный ряд. Обратное, вообще говоря, неверно.
Обозначим суммы положительных и отрицательных членов частичной суммы соответственно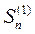 
и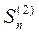 
. Тогда частичная сумма данного ряда
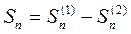, (2)
а частичная сумма ряда, образованного из абсолютных величин членов ряда будет равна
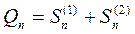. (3)
По условию теоремы существует предел (3), следовательно, существуют пределы 
и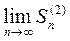 
.
Отсюда следует, что будет существовать и предел (2), ч.т.д.
Замечание 2. Обратное не всегда имеет место. Так, в примере 6 ряд сходится, однако ряд, составленный из положительных величин членов ряда, является расходящимся как гармонический. В примере 7 ряд сходится, сходится и ряд, составленный из абсолютных величин членов ряда, в чём легко убедится, сравнив его с обобщенным гармоническим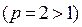 
.
Определение 3. Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд, составленный из абсолютных величин его членов. Если же знакопеременный ряд сходится, а ряд, составленный из абсолютных величин его членов, расходится, то такой ряд называется условно сходящимся.
Таким образом, в примере 6 ряд является условно сходящимся, а в примере 7 - ряд абсолютно сходящийся.
Замечание 3. Следует отметить, что разделение рядов на абсолютно и условно сходящиеся является существенным, что видно из следующих свойств:
1. Если ряд сходится абсолютно, то он остаётся абсолютно сходящимся при любой перестановке его членов. При этом сумма не зависит от порядка его членов.
2. Если ряд сходится условно, то какое бы не было число А, в том числе и бесконечность, можно переставить члены этого ряда, чтобы его сумма оказалась равной А.
3. Если два ряда сходятся абсолютно, то их произведение - также абсо-лютно сходящийся ряд, сумма которого равна произведению сумм этих рядов.
Для условно сходящихся рядов свойство 3 не выполняется.
СПИСОК ЛИТЕРАТУРЫ
1. Беклемишев Д.В. Курс аналитической геометрии и линейной алгебры. – М.: Наука, 1976.
2. Берман Г.Н. Сборник задач по курсу математического анализа. – М.: Наука, 1971.
3. Бермант А.Ф., Араманович И.Г. Краткий курс математического анализа. – М.: Наука, 1971.
4. Бугров Я.С., Никольский С.М. Элементы линейной алгебры и аналитической геометрии. – М.: Наука, 1980.
5. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. – М.: Наука, 1984.
6. Бугров Я.С., Никольский С.М. Дифференциальные уравнения. Кратные интегралы. Ряды. Функции комплексного переменного. – М.: Наука, 1981.
7. Дюженкова Л.І., Дюженкова О.Ю., Михалін Г.О. Вища математика. Приклади і задачі. – К.: Академія, 2003.
8. Задачи и упражнения по математическому анализу./ Под ред. Демидовича Б.П. – М.: Наука, 1972.
9. Збірник задач з вищої математики / За ред. Гудименка Ф.С. – К., 1967.
10. Пак В.В., Носенко Ю.Л. Вища математика. – Донецьк: Видавництво “Сталкер“, 2003.
11. Пискунов Н.С. Дифференциальное и интегральное исчисления. – В 2-х т.– М.: Наука, 1978.
12. Щипачев В.С. Высшая математика. – М.: Высшая школа, 1990.
С О Д Е Р Ж А Н И Е
Предисловие . . . . . . . . . . . . . . . . . . . . . . . . . . 3
Лекция № 1. Тема: Определители . . . . . . . . . . . . . . . . 4
Определители второго и третьего порядков . . . . . . . . . . 4
Основные свойства определителей . . . . . . . . . . . . . . 5
Вычисление определителей . . . . . . . . . . . . . . . . . 6
Лекция № 2. Тема: Системы линейных алгебраических уравнений . . 8
Правило Крамера . . . . . . . . . . . . . . . . . . . . . 8
Метод Гаусса . . . . . . . . . . . . . . . . . . . . . . . 10
Лекция № 3. Тема: Матрицы . . . . . . . . . . . . . . . . . . 13
Основные виды матриц . . . . . . . . . . . . . . . . . . 13
Действия над матрицами . . . . . . . . . . . . . . . . . . 14
Обратная матрица . . . . . . . . . . . . . . . . . . . . . 15
Решение систем линейных уравнений
с помощью обратной матрицы . . . . . . . . . . . . 16
Лекция № 4. Тема: Векторы . . . . . . . . . . . . . . . . . . 18
Определение вектора . . . . . . . . . . . . . . . . . . . . 18
Линейные операции над векторами . . . . . . . . . . . . . 18
Декартова система координат . . . . . . . . . . . . . . . . 20
Лекция № 4. Тема: Векторы (окончание) . . . . . . . . . . . . . 23
Способы задания векторов . . . . . . . . . . . . . . . . . 23
Тема : Скалярное произведение . . . . . . . . . . . . 24
Скалярное произведение двух векторов
и его основные свойства . . . . . . . . . . . . . . 24
Скалярное произведение векторов,
заданных координатами . . . . . . . . . . . . . . . 25
Длина вектора. Угол между двумя векторами.
Направляющие косинусы . . . . . . . . . . . . . . . 25
Лекция № 6. Тема: Векторное произведение . . . . . . . . . . . 27
Векторное произведение двух векторов
и его основные свойства . . . . . . . . . . . . . . 27
Векторное произведение векторов,
заданных координатами . . . . . . . . . . . . . . . 27
Механический смысл векторного произведения . . . . . . . . 28
Тема : Смешанное произведение . . . . . . . . . . . 29
Смешанное произведение двух векторов
и его основные свойства . . . . . . . . . . . . . . . 29
Смешанное произведение векторов,
заданных координатами . . . . . . . . . . . . . . . 30
Лекция № 7. Тема: Линии на плоскости и их уравнения . . . . . . 32
Линии и их уравнения в декартовой системе координат . . . . 32
Параметрические уравнения линии . . . . . . . . . . . . . 32
Уравнение линии в полярной системе координат . . . . . . . 33
Преобразование системы координат.
Уравнение линии в новой системе координат . . . . . . 34
Лекция № 8. Тема: Прямая линия на плоскости . . . . . . . . . . 36
Уравнения прямой линии . . . . . . . . . . . . . . . . . . 36
Угол между двумя прямыми . . . . . . . . . . . . . . . . 37
Взаимное расположение двух прямых . . . . . . . . . . . . 38
Уравнение прямой, проходящей через две точки . . . . . . . 38
Уравнение прямой, проходящей через точку
с заданным угловым коэффициентом . . . . . . . . . 39
Расстояние от точки до прямой . . . . . . . . . . . . . . . 39
Лекция № 9. Тема: Линии второго порядка . . . . . . . . . . . . 40
Эллипс . . . . . . . . . . . . . . . . . . . . . . . . . . 40
Гипербола . . . . . . . . . . . . . . . . . . . . . . . . 42
Парабола . . . . . . . . . . . . . . . . . . . . . . . . . 43
Классификация линий второго порядка . . . . . . . . . . . . 44
Лекция № 10. Тема: Плоскость . . . . . . . . . . . . . . . . . 45
Уравнение плоскости. Построение плоскости . . . . . . . . . 45
Уравнение плоскости, проходящей через заданную точку,
перпендикулярно заданному вектору . . . . . . . . . . 45
Уравнение плоскости, проходящей через
три заданные точки . . . . . . . . . . . . . . . . . 46
Угол между двумя плоскостями . . . . . . . . . . . . . . . 46
Расстояние от точки до плоскости . . . . . . . . . . . . . 47
Тема : Прямая в пространстве . . . . . . . . . . . . . 48
Уравнение прямой . . . . . . . . . . . . . . . . . . . . . 48
Лекция № 11. Тема: Прямая в пространстве (окончание) . . . . . . 49
Уравнение прямой, проходящей через две точки . . . . . . . 49
Угол между двумя прямыми . . . . . . . . . . . . . . . . 49
Расстояние от точки до прямой . . . . . . . . . . . . . . . 50
Угол между прямой и плоскостью . . . . . . . . . . . . . . 51
Пересечение прямой с плоскостью . . . . . . . . . . . . . . 51
Лекция № 12. Тема: Поверхности . . . . . . . . . . . . . . . . 53
Уравнение поверхности . . . . . . . . . . . . . . . . . . 53
Поверхности второго порядка . . . . . . . . . . . . . . . . 54
Лекция № 13. Тема: Функции . . . . . . . . . . . . . . . . . . 58
Определение функции . . . . . . . . . . . . . . . . . . . 58
Способы задания функции . . . . . . . . . . . . . . . . . 59
Элементарные функции . . . . . . . . . . . . . . . . . . 61
Лекция № 14. Тема: Пределы . . . . . . . . . . . . . . . . . . 62
Предел последовательности и переменной величины . . . . . 62
Предел функции . . . . . . . . . . . . . . . . . . . . . 64
Лекция № 15. Тема: Пределы (продолжение) . . . . . . . . . . . 65
Бесконечно малые и бесконечно большие величины . . . . . 65
Теорема о пределе функции . . . . . . . . . . . . . . . . 66
Основные теоремы о пределах . . . . . . . . . . . . . . . 67
Раскрытие неопределенностей . . . . . . . . . . . . . . . 68
Лекция № 16. Тема: Пределы (окончание) . . . . . . . . . . . . 69
Первый стандартный предел . . . . . . . . . . . . . . . . 69
Число е . . . . . . . . . . . . . . . . . . . . . . . . . . 70
Второй стандартный предел . . . . . . . . . . . . . . . . 70
Сравнение б.м.в. . . . . . . . . . . . . . . . . . . . . . 72
Лекция № 17. Тема: Непрерывность . . . . . . . . . . . . . . . 73
Определение непрерывной функции . . . . . . . . . . . . . 73
Основные теоремы о непрерывных функциях
Непрерывность элементарных функций . . . . . . . . 74
Классификация точек разрыва функции . . . . . . . . . . . 74
Свойства функций, непрерывных на отрезке . . . . . . . . . 75
Лекция № 18. Тема: Производная и дифференциал . . . . . . . . 77
Производная функции . . . . . . . . . . . . . . . . . . . 77
Производные основных элементарных функций . . . . . . . . 78
Механический смысл производной . . . . . . . . . . . . . 79
Геометрический смысл производной . . . . . . . . . . . . . 79
Правила дифференцирования . . . . . . . . . . . . . . . . 80
Производная сложной функции . . . . . . . . . . . . . . . 81
Лекция № 19. Тема: Производная и дифференциал (окончание) . . . 82
Производная обратной функции . . . . . . . . . . . . . . 82
Производная функции, заданной параметрическими
уравнениями . . . . . . . . . . . . . . . . . . . 82
Производная функции, заданной неявно . . . . . . . . . . . 83
Производная степенно-показательной функции . . . . . . . . 83
Производные высших порядков . . . . . . . . . . . . . . 84
Дифференциал функции . . . . . . . . . . . . . . . . . . 85
Лекция № 20. Тема : Основные теоремы о дифференцируемых
функциях . . . . . . . . . . . . . . . . . 87
Теорема Ролля . . . . . . . . . . . . . . . . . . . . . . 87
Теорема Лагранжа . . . . . . . . . . . . . . . . . . . . 87
Правило Лопиталя . . . . . . . . . . . . . . . . . . . . . 88
Формула Тейлора . . . . . . . . . . . . . . . . . . . . . 89
Лекция № 21. Тема: Исследование функции . . . . . . . . . . . . 91
Возрастание и убывание функций . . . . . . . . . . . . . 91
Экстремум функции. Необходимые условия экстремума . . . . 91
Достаточные условия экстремума . . . . . . . . . . . . . . 92
Наибольшее и наименьшее значение функции на отрезке . . . 94
Лекция № 22. Тема: Исследование функции (продолжение) . . . . . 95
Выпуклость, вогнутость, точки перегиба . . . . . . . . . . . 95
Асимптоты линий . . . . . . . . . . . . . . . . . . . . . 96
Общий план исследования функции и
построение графиков . . . . . . . . . . . . . . . . 97
Лекция № 23. Тема: Исследование функции (окончание) . . . . . . 99
Исследование функции (пример) . . . . . . . . . . . . . . 99
Кривизна кривой . . . . . . . . . . . . . . . . . . . . . 100
Лекция № 24. Тема: Неопределенный интеграл . . . . . . . . . . 103
Первообразная и неопределенный интеграл . . . . . . . . . 103
Основные свойства неопределённого интеграла . . . . . . . . 104
Таблица неопределённых интегралов . . . . . . . . . . . . 104
Интегрирование методом замены переменной
(способ подстановки) . . . . . . . . . . . . . . . . 105
Лекция № 26. Тема: Неопределенный интеграл (продолжение) . . . 107
Интегрирование некоторых функций,
содержащих квадратный трёхчлен . . . . . . . . . . . 107
Интегрирование по частям . . . . . . . . . . . . . . . . . 108
Многочлены и рациональные дроби . . . . . . . . . . . . . 109
Лекция № 26. Тема: Неопределенный интеграл (продолжение) . . . 111
Интегрирование рациональных дробей . . . . . . . . . . . . 111
Интегрирование тригонометрических функций . . . . . . . . 112
Лекция № 27. Тема: Неопределенный интеграл (окончание) . . . . 114
Интегрирование некоторых иррациональных функций . . . . . 114
Понятие о неберущихся интегралах . . . . . . . . . . . . . 117
Лекция № 28. Тема: Определенный интеграл . . . . . . . . . . . 118
Задачи, приводящие к понятию определённого интеграла . . . 118
Определение определённого интеграла . . . . . . . . . . . . 119
Основные свойства определённого интеграла . . . . . . . . . 120
Интеграл как функция верхнего предела . . . . . . . . . . . 122
Лекция № 29. Тема: Определенный интеграл (окончание) . . . . . . 122
Формула Ньютона – Лейбница . . . . . . . . . . . . . . . . 122
Замена переменной в определённом интеграле . . . . . . . . 123
Интегрирование по частям в определённом интеграле . . . . . 125
Лекция № 30. Тема: Приложения определенного интеграла . . . . . 126
Площадь плоской фигуры . . . . . . . . . . . . . . . . . 126
Длина дуги плоской кривой . . . . . . . . . . . . . . . . 128
Площадь поверхности тела вращения . . . . . . . . . . . . 129
Вычисление объёма тела по площадям поперечных сечений . . 130
Лекция № 31. Тема : Приложения определенного интеграла
(окончание) . . . . . . . . . . . . . . . . . 131
Приложения определённого интеграла к некоторым
задачам физики . . . . . . . . . . . . . . . . . . . 131
Тема: Несобственные интегралы . . . . . . . . . . 132
Несобственные интегралы первого рода
(с бесконечными пределами) . . . . . . . . . . . . . 132
Несобственные интегралы второго рода
(от разрывных функций) . . . . . . . . . . . . . . 134
Лекция № 32. Тема : Функции нескольких переменных. Предел.
Непрерывность. Частные производные . . . . 136
Определение функции нескольких переменных . . . . . . . . 136
Предел и непрерывность функции двух переменных . . . . . 137
Частные производные функции двух переменных . . . . . . . 138
Полный дифференциал функции двух переменных . . . . . . 139
Производная сложной функции . . . . . . . . . . . . . . . 140
Лекция № 33. Тема : Частные производные.
Производная по направлению. Градиент . . . . 141
Полная производная . . . . . . . . . . . . . . . . . . . . 141
Частные производные функции, заданной неявно . . . . . . . 141
Частные производные высших порядков . . . . . . . . . . . 141
Производная по направлению . . . . . . . . . . . . . . . . 142
Градиент . . . . . . . . . . . . . . . . . . . . . . . . . 143
Лекция № 34. Тема : Частные производные. Производная по
направлению. Градиент (окончание) . . . . . . 145
Касательная и нормаль к поверхности . . . . . . . . . . . . 145
Тема : Векторная функция скалярного аргумента . . . 146
Векторная функция. Предел. Непрерывность . . . . . . . . . 146
Производная векторной функции . . . . . . . . . . . . . . 147
Лекция № 35. Тема: Экстремум функции нескольких переменных . . 149
Необходимые условия экстремума . . . . . . . . . . . . . . 149
Достаточные условия экстремума . . . . . . . . . . . . . . 150
Нахождение наибольшего и наименьшего значений
функции в замкнутой области . . . . . . . . 151
Лекция № 36. Тема: Экстремум функции нескольких переменных
(окончание) . . . . . . . . . . . . . . . . . 153
Условный экстремум . . . . . . . . . . . . . . . . . . . 153
Метод наименьших квадратов . . . . . . . . . . . . . . . 156
Лекция № 37. Тема: Дифференциальные уравнения. Введение . . . 158
Задачи, приводящие к дифференциальным уравнениям . . . . 158
Определение дифференциального уравнения. . . . . . . . . . 158
Тема : Дифференциальные уравнения первого порядка . 159
Общие понятия. Теорема существования и единственности . . . 159
Уравнения с разделяющимися переменными . . . . . . . . . 160
Лекция № 38. Тема: Дифференциальные уравнения первого порядка
(окончание) . . . . . . . . . . . . . . . . . 162
Однородные уравнения . . . . . . . . . . . . . . . . . . . 162
Линейные уравнения первого порядка . . . . . . . . . . . . 164
Уравнения Бернулли . . . . . . . . . . . . . . . . . . . . 164
Уравнения в полных дифференциалах . . . . . . . . . . . . 165
Лекция № 39. Тема: Дифференциальные уравнения высших порядков . 167
Определение ДУ п-го порядка . . . . . . . . . . . . . . . 167
Уравнения, допускающие понижение порядка. . . . . . . . . 168
Тема : Линейные дифференциальные уравнения
второго порядка . . . . . . . . . . . . . . 169
Линейные однородные дифференциальные уравнения второго
порядка (ЛОДУ-2). Определитель Вронского
и его свойства . . . . . . . . . . . . . . . 169
Теорема о структуре общего решения ЛОДУ-2 . . . . . . . . 171
Лекция № 40. Тема: Дифференциальные уравнения второго порядка
(продолжение). . . . . . . . . . . . . . . . 172
ЛОДУ-2 с постоянными коэффициентами. . . . . . . . . . . 172
Линейные неоднородные дифференциальные уравнения
второго порядка . . . . . . . . . . . . . . 173
Метод вариаций произвольных постоянных . . . . . . . . . 175
Лекция № 41. Тема: Дифференциальные уравнения второго порядка
(окончание) . . . . . . . . . . . . . . . . . 176
ЛНДУ-2 с постоянными коэффициентами
со специальной правой частью . . . . . . . . 176
Лекция № 42. Тема: Линейные дифференциальные уравнения
высших порядков . . . . . . . . . . . . . 180
Линейные ДУ п-го порядка . . . . . . . . . . . . . . . . 180
Понятие о краевой задаче . . . . . . . . . . . . . . . . . 182
Лекция № 43. Тема: Системы дифференциальных уравнений . . . . 184
Нормальные системы дифференциальных уравнений . . . . . 184
Решение нормальных систем ДУ методом исключений . . . . 186
Лекция № 44. Тема: Числовой ряд.
Необходимый признак сходимости . . . . . . 189
Числовой ряд и его сумма . . . . . . . . . . . . . . . . . 189
Необходимый признак сходимости. Гармонический ряд . . . . 191
Тема : Достаточные признаки сходимости рядов
с положительными членами . . . . . . . . . 192
Признаки сравнения . . . . . . . . . . . . . . . . . . . . 192
Лекция № 45. Тема : Достаточные признаки сходимости рядов
с положительными членами (окончание) . . . . 193
Признак Даламбера . . . . . . . . . . . . . . . . . . . . 193
Радикальный признак Коши . . . . . . . . . . . . . . . . 194
Интегральный признак Коши . . . . . . . . . . . . . . . . 195
Тема : Знакопеременные ряды . . . . . . . . . . . . 196
Знакочередующиеся ряды. Теорема Лейбница . . . . . . . . . 196
Абсолютная и условная сходимость . . . . . . . . . . . . . 197
Л и т е р а т у р а . . . . . . . . . . . . . . . . . . . . . . . 198