 |
|
Некоторые геометрические приложения определенного интеграла
1 Вычисление площадей плоских фигур
 Вычисление площади плоской фигуры в декартовой системе координат.
Вычисление площади плоской фигуры в декартовой системе координат.
Если на сегменте [a,b] непрерывная функция f(x) ³ , то площадь криволинейной трапеции, ограниченной кривой y = f(x), осью Oх и прямыми х = а и x = b, равна определенному интегралу
 .
.
В общем случае, если фигура, представляет собой часть плоскости, ограниченной непрерывными кривыми  ,
,  , (
, (  ) и двумя отрезками прямых x = a, x = b (отрезки прямых могут вырождаться в точку), то площадь такой фигуры можно представить в виде суммы и (или) разности площадей криволинейных трапеций.
) и двумя отрезками прямых x = a, x = b (отрезки прямых могут вырождаться в точку), то площадь такой фигуры можно представить в виде суммы и (или) разности площадей криволинейных трапеций.

 у
у


 |
S

О a  b x
b x
Для вычисления площади такой фигуры будем иметь формулу
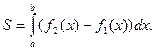
Пример.Найти площадь фигуры, ограниченной линиями: 
 Решение.Сделаем схематический чертеж. Построим данные линии.
Решение.Сделаем схематический чертеж. Построим данные линии.
 у
у


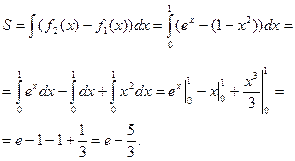 1 х
1 х
Пусть кривая, ограничивающая криволинейную трапецию сверху, задана параметрическими уравнениями  причем
причем 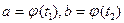 . Тогда площадь фигуры D может быть вычислена по формуле
. Тогда площадь фигуры D может быть вычислена по формуле

 Вычисление площади в полярной системе координат.
Вычисление площади в полярной системе координат.
Пусть плоская фигура D расположена в полярной системе координат и представляет собой криволинейный сектор, ограниченный непрерывной кривой 
 и отрезками лучей j = a и j = b. Отрезки лучей могут вырождаться в точку. Тогда площадь фигуры вычисляется по формуле
и отрезками лучей j = a и j = b. Отрезки лучей могут вырождаться в точку. Тогда площадь фигуры вычисляется по формуле

Пример.Найти площадь фигуры, ограниченной кардиоидой
Решение. Область определения функции будет 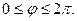


Упражнения
Найти площади фигур, ограниченных линиями.
1.  и осью Ох. 2.
и осью Ох. 2. 
3.  4.
4. 
5.  6.
6. 
7.  8.
8. 
9.  10.
10. 
11. Найти площадь фигуры, ограниченной осью Ох и одной аркой циклоиды 
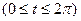 .
.
12. Найти площадь фигуры, ограниченной кривой 
13. Найти площадь фигуры, ограниченной кривой 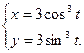
14. Найти площадь фигуры, ограниченной линиями  ,
, 
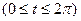 .
.
15. Найти площадь фигуры, ограниченной линиями 
16. Найти площадь фигуры, ограниченной кривой 
17. Найти площадь одного лепестка кривой  .
.
18. Найти площадь фигуры, ограниченной линиями 
19. Найти площадь фигуры, ограниченной линиями 