Главная | Обратная связь

Круглим хвилеводом називається циліндричний хвилевід поперечний перетин якого є круг.

Розв’язати електродинамічну задачу для лінії передачі – це значить знайти в кожній точці лінії в будь-який момент часу вектори електромагнітного поля Е, Н і фазову сталу хвилі. Ця задача розв’язується звичайно таким чином:

1. Вводиться узагальнена циліндрична система координат, вісь z якої спрямована вздовж осі лінії передачі;

- розглядаються хвилі, що поширюються уздовж z.

Тому залежність компонентів поля від повздовжної координати, відповідно до методу комплексних амплітуд, має вигляд

,

де - фазова стала електромагнітної хвилі у хвилеводі;

- уявна одиниця;

Λ - довжина хвилі в хвилеводі.

Фазова стала β – величина, що показує зміну фази хвилі при проходженні нею відстані в один метр (у системі СІ).

2. Записують систему рівнянь Максвела для комплексних амплітуд

 

(6.1)

 

Це система з двох векторних рівнянь з невідомими В і Е.

3. Її проектують на осі координат і одержують систему із шести скалярних рівнянь із шістьма невідомими: чи – у декартовій і циліндричній системі координат відповідно. Потім з отриманої системи виключають поперечні компоненти і, у випадку регулярного хвилеводу, заповненого ізотропним середовищем, приходять до системи з двох рівнянь із двома невідомими – .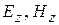

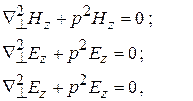(6.2)

де – поперечний оператор Лапласа;

– поперечне хвильове число;

– фазова стала хвилі у вільному просторі;

– довжина хвилі у вільному просторі.

Звідси бачимо, що система розпалася на два незалежних рівняння (у перше входить тільки невідома Н_z, а в друге – E_z). Це вказує на існування в лінії передачі двох незалежних класів хвиль: поперечно-електричних або магнітних – TE_mn (H_mn), у яких , і поперечно-магнітних або електричних – TМ_mn (Е_mn), у яких , .

Рівняння (6.2) називаються хвильовими. Розв’язання кожного з них, разом з відповідними граничними умовами, дозволяє знайти подовжню складову електромагнітного поля (E_z чи Н_z) і фазову сталу хвилі β. Поперечні компоненти знаходяться зі співвідношень, які пов’язують поперечні компоненти поля з повздовжніми:

(6.3)

 

Ці співвідношення можуть бути отримані із системи рівнянь (6.1).

У рівняннях (6.1) і (6.3) входять диференціальні оператори, вирази для яких у циліндричній системі координат подані в додатку.

 

Круглий хвилевід

У круглому хвилеводі, як випливає з теорії, поширюються два класи хвиль: поперечно електричні і поперечно магнітні . Хвилі відрізняються одна від одної конфігурацією поля, фазовою швидкістю й критичною частотою. Хвиля з найнижчою критичною частотою називається основною хвилею хвилеводу, інші – вищими типами.

Розглянемо круглий хвилевід радіуса а, показаний на рис. 6.1. Компоненти поля шукаємо в циліндричній системі координат, у якій координати задаються трійкою чисел – r, θ, z.

 

Рис. 6.1. Циліндричний хвилевід кругового перетину

Завдання полягає в знаходженні фазової сталої хвилі β і складових електромагнітного поля в будь-якій точці простору всередині хвилеводу (r<a).

Можна вважати, що у хвилеводі поширюється одна із поперечних електричних хвиль, що біжить уздовж осі z, а сам хвилевід виконаний з ідеального металу, тобто втрати в металевих стінках відсутні.

Для знаходження залежності компонент поля хвиль класу від поперечних координат необхідно знайти корені хвильового рівняння для разом із граничними умовами на стінці хвилеводу.

 

; . (6.4)

 

Розв’язуючи рівняння (6.4) водночас із граничними умовами, знаходимо подовжню складову магнітного поля й поперечне хвильове число:

 

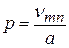; (6.5)

m = 0, 1, 2, 3, …, n = 1, 2, 3, … .

де 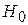– амплітуда подовжньої складового магнітного поля;

– корені рівняння ;

– функція Бесселя;

– похідна функції Бесселя.

Індекс m показує кількість періодів тригонометричної функції при зміні перемінної на , а індекс n – номер кореня рівняння . Фізичний зміст констант mіn – кількість варіацій поля вздовж координат φ та r відповідно. У табл. 1 подані кілька перших коренів ν_mn для різних значень m.

 

Таблиця 6.1. Корені рівняння

n m
	3.821 1.841 3.054 4.201	7.016 5.331 6.706 8.015	10.173 8.536 9.969 11.346	13.324 11.706 13.170

 

Таблиця 6.2. Корені рівняння

n m
	2.405 3.832 5.136 6.380	5.520 7.016 8.417 9.761	8.654 10.173 11.620 13.015	11.792 13.324 14.796 16.223

 

Після обчислення подовжньої складової магнітного поля поперечні компоненти можуть бути виражені через за допомогою співвідношень (6.3):

(6.6)

 

Кожній парі констант m, n відповідає конкретна хвиля типу ТЕ, тому що індексів m і n нескінченна безліч, то і хвиль нескінченна кількість. Однак поширюватися вздовж хвилеводу може тільки кінцева кількість хвиль, а саме ті, критичні частоти яких нижче частоти електромагнітної хвилі.

Критична довжина хвилі і довжина хвилі у хвилеводі, при заданих значеннях m і n, можуть бути знайдені з виразів:

 

, . (6.7)

Для хвиль класу ТМ гранична задача розв’язується аналогічно, але замість рівняння (6.4) записують хвильове рівняння й граничні умови для подовжньої складової електричного поля :

 

(6.8)

 

Розв’язуючи це рівняння водночас із граничними умовами, знаходимо подовжню складову електричного поля й поперечне хвильове число:

 

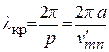, , m = 0, 1, 2, 3, …, n = 1, 2, 3, … , (6.9)

 

де – амплітуда подовжньої складового електричного поля;

– корені рівняння (табл. 6.2).

Поперечні компоненти можуть бути виражені через , як і в попередньому випадку, за допомогою співвідношень (6.3).

(6.10)

Хвиль і нескінченна безліч. Вони відрізняються одна від одної конфігурацією поля й критичною частотою. Хвиля з найнижчою критичною частотою називається основною хвилею лінії передачі. З формул (6.5), (6.9) і табл. 6.2 випливає, що найбільшу критичну довжину має хвиля (ТЕ один, один). Отже, вона і є основною хвилею круглого хвилеводу. Критична довжина цієї хвилі

 

.