 |
|
Теореми заміщення і анулювання
Теорема (заміщення). Сума добутків алгебраїчних доповнень будь якого рядка (стовпця) на довільні числа 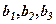 дорівнює новому визначнику, в якому цими числами заміщені відповідні елементи початкового визначника, що відповідають даним алгебраїчним доповненням.
дорівнює новому визначнику, в якому цими числами заміщені відповідні елементи початкового визначника, що відповідають даним алгебраїчним доповненням.
Наприклад,
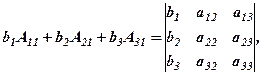
де 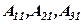 - алгебраїчні доповнення елементів
- алгебраїчні доповнення елементів 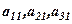 першого стовпця початкового визначника:
першого стовпця початкового визначника:

Теорема (анулювання). Сума добутків елементів одного рядка (стовпця) на алгебраїчні доповнення відповідних елементів іншого рядка (стовпця) дорівнює нулю.
Наприклад,

Дійсно, за теоремою про заміщення ліва частина виразу дасть новий визначник з двома однаковими стовпцями.
Приклад
Для визначника

а) Знайти алгебраїчні доповнення всіх його елементів.
б) Перевірити теорему про розклад для всіх трьох стовпців.
в) Перевірити теорему про анулювання для алгебраїчних доповнень елементів І-го рядка та відповідних елементів ІІ-го рядка, а тоді для елементів ІІІ-го рядка.
Розв’язання
а) 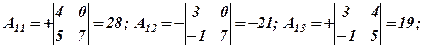
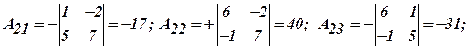
 Часто подібні результати зручно записувати у вигляді таблиці (матриці):
Часто подібні результати зручно записувати у вигляді таблиці (матриці):

б) 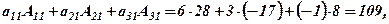
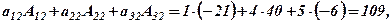
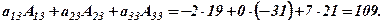
в)
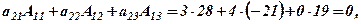

Вправи
Обчислити визначники згідно з означенням

Обчислити визначники за теоремою про розклад
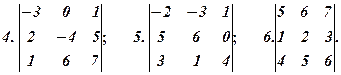
Знайти алгебраїчні доповнення для елементів поданих визначників, перевіряючи їх вірність за допомогою теореми розкладу та теореми анулювання. Значення алгебраїчних доповнень записати у вигляді таблиць (матриць).
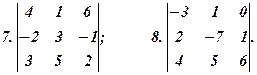
Спростити вирази
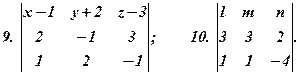
Розв’язати рівняння

Користуючись властивостями визначників спростити вирази::
12. 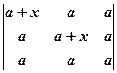 . 13.
. 13. 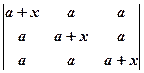 .
.
14.  . 15.
. 15. 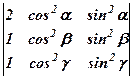 .
.
Користуючись лише властивостями визначника (не розгортаючи їх), розв’язати рівняння:
16. 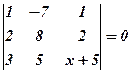 . 17.
. 17. 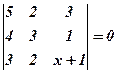
Довести рівність
18. 
Відповіді

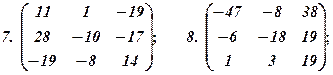
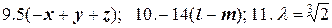
12.  . Вказівка. Відняти останній стовпець від перших двох.
. Вказівка. Відняти останній стовпець від перших двох.
13. 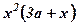 . Вказівка. Відняти від першого стовпця другий, а від другого третій. 14.
. Вказівка. Відняти від першого стовпця другий, а від другого третій. 14.  . Вказівка. Відняти від першого рядка другий, від другого третій. 15.
. Вказівка. Відняти від першого рядка другий, від другого третій. 15. 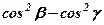 . Вказівка. До третього стовпця додати другий. 16.
. Вказівка. До третього стовпця додати другий. 16. 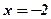 .
.
17. 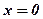 .
.