 |
|
Приведем основные теоремы о сходящихся числовых рядах.
Неделя 14
Лекция 27
Числовые ряды, их свойства и признаки сходимости.
Определение 1. Пусть 
, где, 
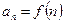— бесконечная числовая последовательность. Выражение
(1)
называется бесконечным числовым рядом, а числа 
членами ряда;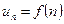 
называется общим членом ряда.
Определение 2. Сумму первых 
членов ряда называют -й частичной суммой и обозначают
(2)
Определение 3. Ряд называется сходящимся, если его -я частичная сумма 
при неограниченном возрастании стремится к конечному пределу, т.е. если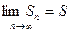 
. Число 
называют суммой ряда. Если же -я частичная сумма ряда при 
не стремится к конечному пределу, то ряд называется расходящимся.
Приведем основные теоремы о сходящихся числовых рядах.
1. Если сходится ряд 
, то сходится и ряд 
, получаемые из данного ряда отбрасыванием первых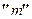 
членов (этот последний ряд называют 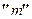-м остатком исходного ряда), наоборот, из сходимости 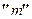-го остатка ряда вытекает сходимость данного ряда.
2. Если сходится ряд , и суммой его является число , то сходится и ряд 
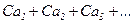, причем сумма последнего ряда равна 
.
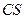3. Если сходятся ряды , 
, имеющие соответственно суммы и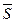 
, то сходится и ряд 
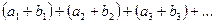, причем сумма последнего ряда равна + .
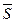4. Если ряд сходится, то 
, т.е. при 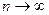предел общего члена сходящего ряда равен нулю (необходимый признак сходимости ряда). Таким образом, если 
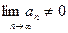, то ряд расходится.
Пример. Рассмотрим ряд, составленный из членов геометрической прогрессии
,
где 
— знаменатель геометрической прогрессии.
-я частичная сумма ряда 
.
Найдем предел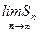 
.
Тогда =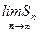 
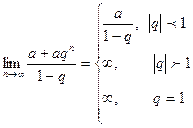
Отсюда имеем, что при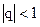 
ряд сходится, а при 
ряд расходится.
Ряды с положительными членами и достаточные признаки сходимости рядов.
Ряд с неотрицательными членами называется рядом с положительными членами
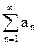- ряд с положительными членами, где 
.
1. Основной признак. Если -я частичная сумма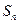 
ряда с положительными членами ограничена сверху, т.е. 
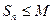, тогда ряд сходится, в противном случае ряд расходится.
2. Признаки сравнения
а) Первый признак сравнения
Пусть даны два ряда с положительными членами:
и 
, (1)
, (2)
причем каждый член ряда (1) не превосходит соответстующего члена ряда (2), т.е.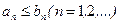 
. Тогда если сходится ряд (2), то сходится и ряд (1); если расходится ряд (1), то расходится и ряд (2).
Этот признак остается в силе, если неравенства 
выполняются не при всех , а лишь начиная с некоторого номера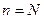 
.
б) второй признак сравнения. Если существует конечный и отличный от нуля предел 
, то оба ряда 
и 
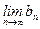одновременно сходятся или одновременно расходятся.
Пример. Исследовать сходимость ряда 
.
Решение. Общий член ряда 
, сравниваем с рядом 
, где общий член 
и выполняется неравенство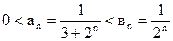 
.
Ряд сходится как бесконечно убывающая геометрическая прогрессия, знаменатель которой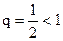 
.
Следовательно, по признаку сравнения и данный ряд сходится.
3. Признак Даламбера. Если для ряда существует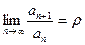 
, то этот ряд сходится при 
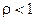и расходится при 
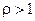, а при 
вопрос остается открытым.
4. Признак Коши. Если для ряда существует 
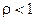, то этот сходится при и расходится при .
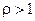Пример. Исследовать сходимость ряда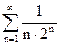 
Решение. Имеем 
, 
исследуем по признаку Даламбера
, ряд сходится.