 |
|
Степенной ряд. Ряд Тейлора.
Определение. Ряд, члены которой являются функцией от 
, т.е. ряд вида
(1)
называется степенным рядом, где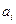 
- коэффициенты степенного ряда действительные числа.
Теорема Абеля. Если степенной ряд (1) сходится в точке 
, то он сходится и притом абсолютно в интервале 
, а если степенной ряд (1) расходится при 
то он расходится и при всяком , большем по абсолютной величине, чем 
, т.е. при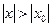 
.
Одним из следствий теоремы Абеля является факт существования для всякого степенного ряда интервала сходимости
 |
Определение. Радиусом сходимости степенного ряда (1) называется такое число 
, что для всех , 
, степенной ряд сходится, а для всех , 
расходится. Интервал 
называется интервалом сходимости.
Для отыскания интервала и радиуса сходимости степенного ряда можно пользоваться одним из следующих способов.
1. Используя признак Даламбера радиус сходимости степенного ряда 
равна
, (2)
при условии, что этот предел (конечный или бесконечный) существует.
2. Используя признак Коши радиус сходимости можно находить по формуле
(3)
Пример. Найти радиус сходимости степенного ряда 
.
Решение. Используя формулу (2) имеем
,
- радиус сходимости данного степенного ряда, то ряд сходится при 
или на промежутке 
.
Ряд Тейлора.
Рассмотрим ряд разложенный по степеням двучлена 
, (4)
Пусть ряд (4) сходится в интервале 
и сумма ряда равна 
, т.е.
(5)
коэффициенты ряда (5) 
выражаются через функцию и ее производные в точке по формулам
, 
(6)
Эти коэффициенты называются коэффициентами Тейлора функции в точке .
Коэффициенты, определяемые формулой (6) подставляем в формулу (5), имеем
(7)
Этот ряд называют рядом Тейлора.
,
где 
- n-я
частичная сумма ряда, а 
- остаточный член ряда Тейлора
, где 
.
В частности, при 
ряд Тейлора имеет вид
(8)
Этот ряд называется рядом Маклорена, его остаточный член равен
.
Примеры. 1. Функцию 
разложить в ряд Маклорена.
Решение. Используя формулу (8) имеем
(9)
Используя формулу (8) имеем разложение следующих функции:
Пример 2. Вычислить 
с точностью до 
.
Решение. Используя разложение 
в ряд, получаем
берем первые четыре члена, т.к. пятый член 
меньше заданной точности , т.е.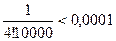 
.
Следовательно 
.