 |
|
Означення. Сполуками з п елементів по k елементів називається будь-яка k–підмножина даної п-множини.
Виведемо формулу, яка виражає С  через п і k. Візьмемо яку-небудь k -підмножину А в п-множині X. Оскільки А містить k елементів, то її можна
через п і k. Візьмемо яку-небудь k -підмножину А в п-множині X. Оскільки А містить k елементів, то її можна
упорядкувати k!способами. При цьому кожна впорядкована k -множина, що складається з елементів множини X, може бути отримана таким шляхом. Значить, число впорядкованих k -множин, складених з елементів множини X, в k!разів більше числа невпорядкованих k -підмножин в X.
Наприклад, з елементів множини А = {а; b; с; d) можна скласти чотири трьохелементних підмножини:
{а; b; с;}, {а; b; d}, {а: c: d}, {b; c; d). Число ж упорядкованих трьохелементних підмножин у 3! = 6 разів більше.
Щоб це побачити і щоб вивести формулу обчислення сполук, розглянемо приклад. Утворимо розміщення А  .
.
(а; b; с) (а; b; d) (а; с; d) (b; с; d)
(а; с; b) (а; d; b) (а; d; с) (b; d; с)
(b; а; с) (b; а; d) (с; а; d) (с; b; d)
{b; с; а) (b; d; а) (с; d; а) (с; d; b)
(с; а; b) (d; а; b) (d; а; с) (d; b; с)
(с; b; а) (d; b; а) (d; с; а) (d; с; b)
Як бачимо, кількість трьохелементних підмножин з 4 елементів склала за правилом прямокутника 24 кортежі. По горизонталі розмістилися усі підмножини, які відрізняються лише складом елементів, тобто сполуки С  . А по вертикалі перестановки Р3. Звідси А
. А по вертикалі перестановки Р3. Звідси А  = С
= С  × Р3. Звідки С
× Р3. Звідки С  =
=  . Таким чином, в загальному вигляді формула обчислення сполук без повторень обчислюється за формулою: С
. Таким чином, в загальному вигляді формула обчислення сполук без повторень обчислюється за формулою: С  .
.
Зважаючи на формулу 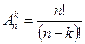 , легко отримати новий вид формули сполук, помноживши знаменник на k!, тобто її вигляд буде С
, легко отримати новий вид формули сполук, помноживши знаменник на k!, тобто її вигляд буде С 
Ця формула виражає число k -підмножин у п-множині X.
Приклад. Скількома способами можна вибрати делегацію з 5 осіб з групи, у 12 осіб?
Оскільки порядок членів делегації ролі не грає, то нам треба дізнатися, скільки можна вибрати 5-тиелементних підмножин з 12-тиелементної множини. Щоб обчислити кількість способів, підставимо данні у формулу С  :
:
Отримаємо: С 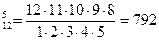 .
.
Властивості чисел С .
.
Властивість 1. С =
= 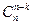 .
.
Нам відомо, що С 
Розкриємо формулу 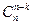 .
. 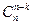 =
=  , тобто отримали ту ж саму формулу. А з цього і випливає вірність нашого твердження.
, тобто отримали ту ж саму формулу. А з цього і випливає вірність нашого твердження.
Властивість 2. С = С
= С 
Дійсно, С  .
. 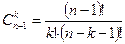 . Помноживши чисельник і знаменник цього виразу на (п – k), отримаємо вираз
. Помноживши чисельник і знаменник цього виразу на (п – k), отримаємо вираз 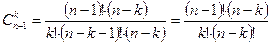 . Виконавши додавання, отримаємо шукане твердження.
. Виконавши додавання, отримаємо шукане твердження.
За допомогою цієї тотожності можна послідовно обчислювати С  спочатку при k = 0, потім при k = 1, при k = 2 і т.д. При цьому слід враховувати, що С
спочатку при k = 0, потім при k = 1, при k = 2 і т.д. При цьому слід враховувати, що С  і С
і С  .Обчислення зручно записувати у вигляді трикутної таблиці, яка у математиці отримала назву „Трикутник Паскаля”. Справа в тому, що ця таблиця зустрічається у працях французького математика й астронома Блеза Паскаля (1623–1662). Однак фактично така таблиця була відома ще арабському математику і поету Омару Хайяму ще у ХІІІ столітті.
.Обчислення зручно записувати у вигляді трикутної таблиці, яка у математиці отримала назву „Трикутник Паскаля”. Справа в тому, що ця таблиця зустрічається у працях французького математика й астронома Блеза Паскаля (1623–1662). Однак фактично така таблиця була відома ще арабському математику і поету Омару Хайяму ще у ХІІІ столітті.
Сутність цієї таблиці полягає в тому, що в п + 1 рядку трикутної таблиці по порядку стоять числа С  , С
, С 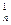 , С
, С  ,..., С
,..., С  . При цьому С
. При цьому С  = С
= С  = 1, а інші числа обчислюються за формулою С
= 1, а інші числа обчислюються за формулою С  = С
= С  .
.
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
Оскільки С  і
і  розташовані у цій таблиці рядком вище, ніж С
розташовані у цій таблиці рядком вище, ніж С  , і знаходяться у цьому рядку зліва і справа від нього, то для отримання С
, і знаходяться у цьому рядку зліва і справа від нього, то для отримання С  треба додати числа попереднього рядка, які знаходяться від нього зліва і справа. Наприклад, значення С
треба додати числа попереднього рядка, які знаходяться від нього зліва і справа. Наприклад, значення С  = 10 отримується шляхом додавання чисел 4 і 6, які знаходяться над числом 10, а щоб знайти С
= 10 отримується шляхом додавання чисел 4 і 6, які знаходяться над числом 10, а щоб знайти С  , яке дорівнює 4 і знаходиться у 5 рядку справа, слід додати числа 3 і 1, які знаходяться над ним.
, яке дорівнює 4 і знаходиться у 5 рядку справа, слід додати числа 3 і 1, які знаходяться над ним.
Вправи
1. Скількома способами можна вибрати чотири фарби з шести різних
фарб?
2. У одного учня є 8 книг з математики, а у іншого – 6 книг. Скількома способами вони можуть обміняти три книги однієї людини на три книги іншої людини?
3. У класі 30 учнів. Скількома способами можна скласти чотири команди по 4 учня для участі в олімпіаді з 4 предметів, якщо з усіх предметів вона проходить одночасно?
4. Скількома способами можна створити з групи у 12 чоловіків і 8 жінок комісію, щоб вона складалася з 3 чоловіків і 4 жінок?
5. Рота складається з трьох офіцерів, 6 сержантів і 60 рядових. Скількома способами можна виділити з них загін, що складається з одного офіцера, двох сержантів і 20 рядових?
6. На шкільному вечорі були присутніми 12 дівчат і 16 хлопців. Скількома способами можна вибрати з них 4 пари для танцю?
7. Скількома способами можна вибрати 12 чоловік з 17, якщо двоє з них Петро і Іван не можуть бути вибрані разом?
8. Скільки діагоналей має 8-микутник?
9.Профспілковий комітет складається з 12 осіб. Мінімальний кворум складається з 8 осіб.
а) Скількома способами може складатися мінімальний кворум?
б) Скількома способами може складатися будь-який кворумний склад?
10. Обчислити значення виразів:а) С  – С
– С 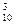 ; б) С
; б) С  + С
+ С 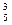 ; в) А
; в) А – С
– С 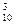 ;
;
г)  ; д)
; д) 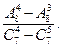
11. З двох партій деталей, з яких в одній було 6 деталей, а у другій 11 взяли деталі на експертизу ВТК: з першої партії 2, а з другої 3. Скількома способами можна це зробити?
12. Розв’язати рівняння: а) С  = 15; б) С
= 15; б) С  + С
+ С  = 49; в) С
= 49; в) С  + С
+ С  = 15(х – 1);
= 15(х – 1);
г) 14  ; д) 21
; д) 21  , е) А
, е) А  10
10 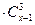
є) С  + С
+ С  =15(х2 –1).
=15(х2 –1).
13. Розв’язати систему рівнянь: 
14. У шаховому гуртку займаються 2 дівчинки і 7 хлопчиків. Для участі у змаганнях необхідно створити команду з 4 гуртківців, в яку обов’язково повинна входити хоча б одна дівчинка. Скількома способами можна це зробити?
15. Три стрільця повинні вразити 15 мішеней (кожний по 5). Скількома способами вони можуть розподілити мішені між собою?
16. Є колода з 36 карт. Скількома способами можна витягнути 6 карт так, щоб:
а) серед них був тільки один туз;
б) щоб було 2 тузи;
в) не було ні одного туза;
г) був хоча б один туз;
д) щоб було хоча б 2 тузи;
е) були тільки один туз і один король;
є) не було ні одного туза і ні одного короля.
ж) були туз і король однієї масті.
17. У лотереї „5 з 36” ті, хто вгадав 4, 3 або 2 номери отримують менший приз, ніж той, хто вгадав 5 номерів. Скільки може бути різних карток, де вгадано:
а) 4 номери; б) 3 номери; в) хоча б 4 номери?
18. Скільки різних дільників має число 2310? (2310 = 2×3×5×7×11)
19. У Миколи 6 друзів. Кожний день він запрошує до себе трьох з них так, щоб компанія ні разу не повторилася. Скільки для цього йому знадобиться днів?
20. Скільки прямих можна провести через 7 точок, які не лежать на одній прямій?
БІНОМ НЬЮТОНА
Добуток біномів, що відрізняються тільки другими членами.Звичайним множенням знаходимо:
(х+а)(x+b) = x2+ax+bx+ab=x2+(a+b)x+ab;
(х+а)(x+b)(х+с)=[х2+(а+b)x+ab](x+c)=x3+(a+b)x2+abx+cx2+(ac+bc)x +
+abc = x3+(a+b+c)х2+(аb + ас + bс)x + abc.
Подібно до цього знайдемо:
(х+а)(х+b)(х+с)(x+d)= x4+(a+b+c+d) х3+(ab+ac+ad+bc+bd+cd)x2+
+(abc+abd+acd+bcd) x+abcd.
Розглядаючи ці твори, помічаємо, що всі вони складені поодинці і тому ж закону, а саме: добуток складає многочлен, розташований по спадаючими ступенях букви X.
Показник першого члена дорівнює числу перемножуваних біномів; показники при х в наступних членах спадають на 1; останній член не містить х (містить його в нульовому ступені).
Коефіцієнт першого члена є 1; коефіцієнт другого члена є сума всіх других членів перемножуваних біномів; коефіцієнт третього члена є сума всіх добутків других членів, узятих по два; коефіцієнт четвертого члена є сума всіх добутків других членів, узятих по троє. Останній член є добуток всіх других членів.
Формула бінома Ньютона. Припустимо, що в доведеній нами рівності
(x+a)(x+b)×...×(x+k)=xm+S1xт-1+S2xт-2+ ...+Sт всі другі члени біномів однакові, тобто що а = b = с = ... = k. Тоділіва частина буде ступінь бінома (х+а)т. Поглянемо, у що перетворяться коефіцієнти Sl, S2, ..., Sт.
Коефіцієнт Sl рівний a+b+c + ...+ k, перетвориться в та. Коефіцієнт S2, рівний ab+ac+ad + ..., перетвориться в число а2, повторене стільки раз, скільки можна скласти сполук з т елементів по2, тобто перетвориться в  а2. Коефіцієнт S3,рівнийabc+acd+abd+..., перетвориться в число а3, повторенестільки раз, скільки можна скласти сполук з т елементів по 3, тобто
а2. Коефіцієнт S3,рівнийabc+acd+abd+..., перетвориться в число а3, повторенестільки раз, скільки можна скласти сполук з т елементів по 3, тобто  а3 і т.д. Нарешті, коефіцієнт Sm,рівнийabc...k, перетворитьсяв am. Таким чином, ми отримаємо: (х+а)т= xm+
а3 і т.д. Нарешті, коефіцієнт Sm,рівнийabc...k, перетворитьсяв am. Таким чином, ми отримаємо: (х+а)т= xm+  аxт-1+
аxт-1+  а2xт-2+
а2xт-2+  а3 xт-3+...+ am.
а3 xт-3+...+ am.
Ця рівність відома як формула бінома Ньютона*, причому многочлен, що стоїть в правій частині формули, називається розкладанням бінома. Розглянемо особливості цього многочлена.
___________________________
*/ Ісаак Ньютон – видатний англійський математик (1642–1727). Формула бінома для цілого, дробового і від’ємного показників була ним виведена біля 1665 р., але строгого доведення він не надав. Таке доведення для цілих додатних показників була доведена Якобом Бернуллі (1654-1705).
Властивості формули бінома Ньютона.З цих властивостей ми вкажемо наступні 10:
1. Показники букви х зменшуються на 1 від першого члена до останнього, причому у першого члена показник х рівний показнику ступеня бінома, а в останньому він є 0; навпаки, показники букви а збільшуються на 1 від першого члена до останнього, причому в першому членові показник при а є 0, а в останньому він рівний показнику ступеня бінома. Внаслідок цього сума показників при х і а в кожному члені одна і та ж, а саме: вона дорівнює показнику ступеня бінома.
2. Число всіх членів розкладання є т + 1, оскільки розкладання містить всі ступені а від 0 до т включно.
3. Коефіцієнти рівні: у першого члена – 1, у другого члена – показнику ступеня бінома, у третього члена – числу сполук з т елементів по 2, у четвертого члена – числу сполук з т елементів по 3; взагалі коефіцієнт (п + 1)-го члена є число сполук з т елементів по п. Нарешті, коефіцієнт останнього члена дорівнює числу сполук з т елементів по т, тобто 1.
Відмітимо, що ці коефіцієнти називаються біноміальними.
4. Позначаючи кожен член розкладання буквою Т з цифрою внизу,
яка вказує номер місця цього члена в розкладанні, тобто перший
член Т1, другий член Т2 і т. д., ми можемо написати: Тп+1 =  ап xт-п
ап xт-п
Ця формула виражає загальний член розкладання, оскільки з неї ми можемо отримати всі члени (окрім першого), підставляючи на місце п числа: 1, 2, 3 ...,т.
5. Коефіцієнт першого члена від початку розкладання дорівнює одиниці, коефіцієнт першого члена від кінця теж дорівнює одиниці. Коефіцієнт
другого члена від початку є т, тобто  , коефіцієнтдругого члена
, коефіцієнтдругого члена
від кінця є  , але оскільки
, але оскільки  , то ці коефіцієнти однакові. Коефіцієнт третього члена від початку дорівнює третьому коефіцієнту від кінця і т.д., тобто, коефіцієнти членів, однаково віддалених від кінців розкладання, рівні між собою.
, то ці коефіцієнти однакові. Коефіцієнт третього члена від початку дорівнює третьому коефіцієнту від кінця і т.д., тобто, коефіцієнти членів, однаково віддалених від кінців розкладання, рівні між собою.
6. Розглядаючи біноміальні коефіцієнти, ми відмічаємо, що оскільки вони розташовані симетрично, то найбільший з них розташований посередині. Якщо показник степеня є число парне, то кількість членів розкладання непарне, тому найбільший коефіцієнт один, якщо ж показник парний, то таких коефіцієнтів 2, оскільки членів розкладання число парне.Наприклад:
(х+а)4 =х4+4ах3+ 6а2х2 + 4а3х + а4;
(х+а)5= х5+5ах4+ 10а2х3 +10а3х2+5а4х+а5.
7) З порівняння двох членів, які стоять рядом, випливає висновок, що
Для отримання коефіцієнта наступного члена досить помножити коефіцієнт попереднього члена на показник букви х в цьому члені і розділити на число членів, передуючих визначуваному.
Користуючись цією властивістю, можна відразу писати, наприклад
(х + а)7 = х7+7х6а + 21х5а2 + 35х4а3 +35х3а4+21х2а5 + 7ха6+ а7
Щоб отримати, скажімо, коефіцієнт третього члена 21, треба у попередньому члені помножити 7 на 6 і результат поділити на 2, тобто на кількість членів, що цьому третьому передують. Наступний 35 отримається так: (21×5):3 і т.д.
8. Сума усіх біноміальних коефіцієнтів дорівнює 2т. Дійсно, поклавши х = а = 1, отримаємо, що сума усіх коефіцієнтів дорівнює 2т. Наприклад, у попередньому прикладі сума коефіцієнтів
1 + 7 + 21 + 35 + 35 + 21 + 7 + 1 = 128 = 27
9) Заменивши у формулі бинома а на –а, отримаємо чергування знаків коефіцієнтів. У нашому прикладі це буде виглядати так:
(х – а)7 = х7–7х6а + 21х5а2 – 35х4а3 +35х3а4–21х2а5 + 7ха6– а7
Від’ємні коефіцієнти будуть у членів, в яких другий член біному а буде у непарному степені.
10) Якщо в останньому випадку покласти х=а=1, то побачимо, що сума коефіцієнтів, які стоять на непарних місцях, дорівнює сумі коефіцієнтів, що стоять на парних місцях.
Вправи для самостійного розв’язання.
1. Знайти за формулою бінома Ньютона:
(х + 1)6; (х + 3)9; (х – 2)8; (5 – а)4; (3х + 2у)5; (2х – 5у)4.
2. 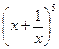 ; (х2+ 2у2)4 ; (3а2– 2b2)6 .
; (х2+ 2у2)4 ; (3а2– 2b2)6 .
3. Знайти 6 член розкладання (5х2–6а2)10; (3а–2)10.
Знайти 8 член розкладання (5х–1)12; (3а+1)10.
4. Обчислити: 2,16 = (2 + 0,1)6. Аналогічно: 1,035; 0,974; 2,84.
5. Обчислити: 295; 313; 993; 824.
6. Обчислити: (4 + 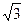 )5; (6 – 5
)5; (6 – 5 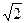 )5; (
)5; (  )4; (
)4; ( 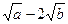 )4;
)4;
(1 + 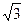 )8; (3
)8; (3 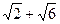 )6.
)6.
7. В розкладанні  обчислити член, який не має х.
обчислити член, який не має х.
8. В розкладанні 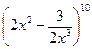 обчислити член, який не має х.
обчислити член, який не має х.
Література:
1. Математика/ Віленин Н.Я., Пишкало А.М., Рождественская В.Б., Стойлова Л.П. – М., Просвещение, 1977. –352 с.
2. Виленкин Н.Я. Комбинаторика/Вилнкин Н.Я., Виленкин А.Н., Виленкин П.А. –М., ФИМА МЦИМО, 2006. –311 с.
3. Проценко Е.А. Теоретические и методические основы изучения комбинаторики в начальной школе /Е.А.Проценко, Г.А.Семёнова. – Таганрог, 2008. – 126 с.
4. Семеновых Г.А. Основные понятия клмбинаторики//Математика в школе. –2004. –№ 15, 16, 17.
5. Стойлова Л.П. Математика. –М.: Академия, 1999. – 422 с.
6. Скачков В.Н. Введение в комбинаторные методы дискретной математики. –М.: Наука, 1982. –162 с.
7. Шлапак Л.В. Елементи комбінаторики/Людмила Шлапак, Людвіг Сморжевський. –Тернопіль: Мандрівець, 2006. – 88 с.