Главная | Обратная связь

Двопроменева модель поширення радіохвиль

Двопроменева модель (рис. 3.2) застосовується у випадках, коли прийнятий сигнал складається з двох складових: прямої хвилі й відбитої від поверхні Землі.

Перша складова визначається з формули втрат при поширенні у вільному просторі (3.33). Відбитий промінь представлений на рис. 3.2 сегментам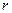и й . Використовуючи метод накладення, одержимо, що прийнятий сигнал у двопроменевій моделі

де — тимчасова затримка відбитого від землі сигналу щодо складової прямого сигналу; R — коефіцієнт відбиття від землі; G_r — результат взаємодії полів з обліком діаграмам спрямованості передавальної й приймальні антен для 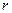й . Якщо переданий сигнал є вузькосмуговим щодо тимчасової затримки то .

Таким чином, потужність прийнятого сигналу для розглянутої моделі

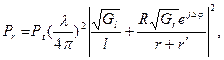(3.33)

де — різниця фаз між двома складовими прийнятого сигналу. Якщо d — відстань між антенами; h_t — висота передавальної антени; - висота прийомної антени, то різниця фаз визначається як:

Рис. 3.2Двопроменева модель поширення радіохвиль

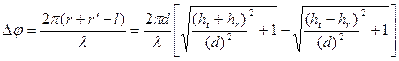. (3.34)

Як було відзначено раніше, рівняння (3.33) добре використовується з емпіричними даними. Розкид по затримці для двопроменевої моделі — це додаткова затримка при відбитті від землі 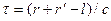. Коефіцієнт земного відбиття визначається

як:

де - для вертикальної й горизонтальної поляризацій відповідно.

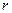- діелектрична постійна поверхні, що для землі або дорожнього покриття приблизно дорівнює діелектричної постійної діелектрика ( = 15).

Якщо d досить велике, те , тоді

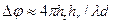
Для асимптотично великого значення d маємо й . Підстановка цих апроксимованих значень у вираження (3.33) показує, що потужність прийнятого сигналу приблизно становить:

. (3.35)

Таким чином, при більших значеннях d потужність прийнятого сигналу зменшується обернено пропорційна четвертому ступеню d.

Апроксимація для критичної відстані d_c може бути отримана шляхом підстановки замість 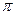в (3.35), що дає d_c = . Отриманий параметр використається при побудові стільникових систем зв’язку для визначення оптимального розміру стільника.

Якщо взяти середнє від максимального й мінімального значень у вираженні (3.33), то отримані втрати потужності можуть бути апроксимовані шляхом розподілу кривих втрат потужності на дві області. Для d < d_c середнє зменшення потужності за відстанню відповідає втратам у вільному просторі. Для зменшення потужності залежить від відстані, що описується законом зменшення обернено пропорційне четвертому ступеню від відстані (3.36).

Ці апроксимації лежать в основі спрощеної моделі для середнього значення прийнятої потужності (при цьому передбачається, що ):

(3.36)

Де - являє собою лінійну апроксимацію зменшення потужності сигналу. Для цієї апроксимації т = 4, тобто має місце експонентне зниження потужності при більших ; — емпірична постійна; q — параметр, що визначає плавність зміни величини втрат на трасі в області переходу поблизу .