 |
|
Направления выпуклости, точки перегиба
График функции  называется выпуклым вниз на интервале
называется выпуклым вниз на интервале  , если он целиком расположен выше любой его касательной на этом интервале.
, если он целиком расположен выше любой его касательной на этом интервале.
График функции  называется выпуклым вверх на интервале
называется выпуклым вверх на интервале  , если он целиком расположен ниже любой его касательной на этом интервале.
, если он целиком расположен ниже любой его касательной на этом интервале.
Теорема.Если во всех точках интервала  вторая производная функции
вторая производная функции  отрицательна, т.е.
отрицательна, т.е.  , то ее график является выпуклым вверх на этом интервале. Если во всех точках интервала
, то ее график является выпуклым вверх на этом интервале. Если во всех точках интервала  вторая производная функции
вторая производная функции  положительна, т.е.
положительна, т.е.  , то ее график является выпуклым вниз на этом интервале.
, то ее график является выпуклым вниз на этом интервале.
Точкой перегиба графика функции  называется такая его точка, в которой выпуклость меняется на противоположную.
называется такая его точка, в которой выпуклость меняется на противоположную.
Необходимое условие существования точки перегиба
Теорема.Если  – точка перегиба функции
– точка перегиба функции  , то в этой точке вторая производная либо равна нулю, либо не существует.
, то в этой точке вторая производная либо равна нулю, либо не существует.
Достаточное условие существования точки перегиба
Теорема.Пусть функция  имеет первую производную в точке
имеет первую производную в точке  и вторую производную в некоторой окрестности этой точки. Тогда если при переходе через точку
и вторую производную в некоторой окрестности этой точки. Тогда если при переходе через точку  вторая производная меняет знак, то
вторая производная меняет знак, то  – точка перегиба.
– точка перегиба.
Пример.
Найти интервалы выпуклости и точки перегиба графика функции  .
.
Решение.
Поскольку вторая производная  обращается в ноль при
обращается в ноль при  и меняет знак при переходе через это значение, например,
и меняет знак при переходе через это значение, например,  , то
, то  – точка перегиба,
– точка перегиба,  . Так как
. Так как 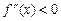 при
при 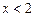 и
и  при
при  , то график функции является выпуклым вверх на интервале
, то график функции является выпуклым вверх на интервале  и выпуклым вниз на интервале
и выпуклым вниз на интервале  .
.
Задачи.
Найти интервалы выпуклости и точки перегиба функций:
7.123. 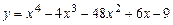 ; 7.124.
; 7.124.  ;
;
7.125.  ; 7.126.
; 7.126.  .
.
Асимптоты
Асимптотой кривой называется прямая, к которой неограниченно приближается данная кривая, когда ее точка неограниченно удаляется от начала координат. Различают асимптоты вертикальные и наклонные.
Прямая  называется вертикальной асимптотой графика функции
называется вертикальной асимптотой графика функции  , если хотя бы одно из предельных значений
, если хотя бы одно из предельных значений  является бесконечным.
является бесконечным.
Прямая  называется наклонной асимптотой графика непрерывной функции
называется наклонной асимптотой графика непрерывной функции  при
при  (
(  или
или  ), если
), если  , где
, где  .
.
График функции  имеет при
имеет при  наклонную асимптоту тогда и только тогда, когда существуют два конечных предела:
наклонную асимптоту тогда и только тогда, когда существуют два конечных предела:  .
.
Пример.
Найти асимптоты графика функции  .
.
Решение.
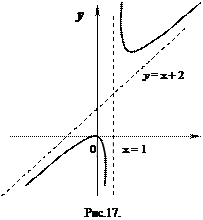
Прямая  является вертикальной асимптотой, так как
является вертикальной асимптотой, так как 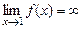 . Поскольку
. Поскольку  и
и  , то график функции имеет и наклонную асимптоту
, то график функции имеет и наклонную асимптоту 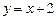 (рис.17).
(рис.17).
 | |||
| |||
Задачи.
Найти асимптоты графиков функций:
7.127.  ; 7.128.
; 7.128.  ;
;
7.129. 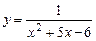 ; 7.130.
; 7.130.  .
.
13. Общий план исследования функции и построение ее графика
При исследовании функции и построении ее графика полезно придерживаться следующей последовательности действий:
1. Найти область определения функции, исследовать ее на концах области определения.
2. Определить возможный тип симметрии: исследовать на четность, нечетность.
3. Найти точки пересечения графика функции с осями координат.
4. Найти вертикальные и наклонные асимптоты.
5. Найти промежутки возрастания, убывания функции и точки экстремума функции.
6. Найти промежутки выпуклости, вогнутости функции и точки перегиба функции.
7. Построить эскиз графика функции с учетом исследования.
Пример.
Исследовать функцию 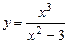 и построить ее график.
и построить ее график.
Решение.
1. Функция не определена при  . Следовательно, область определения состоит из трех интервалов:
. Следовательно, область определения состоит из трех интервалов:  . При стремлении аргумента к концам области определения соответственно получаем:
. При стремлении аргумента к концам области определения соответственно получаем:  .
.
2. Функция нечетная, т.к.  . Значит, график ее будет симметричен относительно начала координат.
. Значит, график ее будет симметричен относительно начала координат.
3.  при
при  .
.
4. Вертикальные асимптоты:  и
и  , так как
, так как 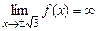 .
.
Найдем наклонные асимптоты:
 ,
,  .
.
Следовательно, наклонная асимптота 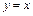 .
.
5. Находим первую производную функции:  .
.  при
при  . Данная функция возрастает при
. Данная функция возрастает при  , т.к. в этих интервалах
, т.к. в этих интервалах  и убывает при
и убывает при 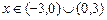 , т.к. в этих интервалах
, т.к. в этих интервалах  . Следовательно, точка
. Следовательно, точка  является точкой максимума (первая производная при переходе через это значение меняет знак с плюса на минус) и
является точкой максимума (первая производная при переходе через это значение меняет знак с плюса на минус) и  , а точка
, а точка  является точкой минимума (первая производная меняет знак с минуса на плюс) и
является точкой минимума (первая производная меняет знак с минуса на плюс) и  .
.
6. Находим вторую производную функции: 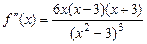 . Так как
. Так как  при
при  , то график функции является выпуклым вверх в этих интервалах. Так как
, то график функции является выпуклым вверх в этих интервалах. Так как 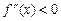 при
при  , то график функции является выпуклым вниз в этих интервалах. Точка
, то график функции является выпуклым вниз в этих интервалах. Точка  является точкой перегиба, т.к. вторая производная меняет знак в окрестности этой точки.
является точкой перегиба, т.к. вторая производная меняет знак в окрестности этой точки.
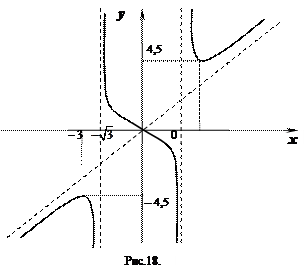
7. Построим график данной функции (рис.18).
Задачи.
Исследовать функции и построить их графики:
7.131.  ; 7.132.
; 7.132.  ;
;
7.133.  ; 7.134.
; 7.134.  ;
;
7.135. 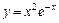 ; 7.136.
; 7.136.  ;
;
7.137.  ; 7.138.
; 7.138.  ;
;
7.139.  ; 7.140.
; 7.140.  ;
;
7.141.  ; 7.142.
; 7.142.  ;
;
7.143. 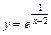 ; 7.132.
; 7.132.  .
.