 |
|
Основные формулы и комментарии к методу наименьших квадратов
Общие сведения
Запишем требования МНК аналитически:
J=  (1.1)
(1.1)
Выражение (1,1) определяет критерий выбора аппроксимирующей функции.
Аппроксимирующую функцию φ(x) выбирают из некоторого семейства функций, для которого задан вид функции, но неизвестны и подлежат определению ее параметры С1, С2, …, Сm.
ϕ (x) = ϕ (x, C1, C2, …, Cm), (1.2)
Определение аппроксимирующей функции φ(x) подразделяется на два основных этапа:
−подбор подходящего вида функции φ(х);
−нахождение параметров функции φ(х) в соответствии с критерием МНК. Подбор вида функции φ(х) представляет собой сложную задачу, решаемую методом проб и последовательных приближений. Исходные данные, представленные в графической форме, сопоставляются c семействами графиков ряда типовых функций, используемых обычно для аппроксимации.
Методика решения
После того как выбран вид аппроксимирующей функции φ(х) и, следовательно, определена функциональная зависимость (1.2), необходимо найти в соответствии с требованиями МНК значения параметров С1, С2, …, Сm.
Как уже указывалось, параметры должны быть определены таким образом, чтобы значение критерия (1.1) было наименьшим.
С учетом (1.2) критерий аппроксимации J, определяемый выражением (1.1) представляется функцией искомых параметров
J = J (С1, С2, …, Сm). (1.3)
Последующие действия сводятся к отысканию минимума функции J, зависящей от переменных Сk. Определение значений Сk = Сk*, k = 1, 2, …, m, соответствующих этому минимуму J, и является целью решаемой задачи.
Возможны следующие два подхода к решению этой задачи:
−использование известных условий минимума функции нескольких переменных;
−непосредственное отыскание точки минимума функции каким-либо из численных методов.
Для реализации первого из указанных подходов воспользуемся необходимыми условиями минимума функции нескольких переменных [2], в соответствии с которыми в точке минимума должны быть равны нулю частные производные этой функции по всем ее переменным:
 (1.4)
(1.4)
Полученные m равенств следует рассматривать как систему уравнений относительно искомых значений С1, С2, …, Сm. При произвольном виде функциональной зависимости (1.2) уравнения (1.4) оказываются нелинейными относительно величин Сk, и их решение требует применения приближенных численных методов.
Используемые равенства (1.4) дают лишь необходимые, но не до- статочные условия минимума функции (1.3). Поэтому требуется уточнить, обеспечивают ли найденные значения Сk* именно минимум функции J(С1, С2, …, Сm). однако, поскольку величина J неотрицательна (как сумма квадратов) и нижняя ее граница равна 0, то, если существующее решение системы (1.4) единственно, оно отвечает именно минимуму J. таким образом, (1.4) является как не- обходимым, так и достаточным условием минимума функции (1.3).
Уравнения (1.4), используемые в МНК, называются нормальными, поэтому описываемый способ решения задачи будем называть методом нормальных уравнений.
Структура этих уравнений получается более простой в том слу- чае, когда аппроксимирующая функция ϕ(x) выбирается линейной функцией искомых параметров Сk и выражение (1.2) имеет вид :
 (1.5)
(1.5)
где Сk – определяемые параметры; ϕ1(x), ϕ2(x), …, ϕm(x) – система линейно-независимых функций, называемых в курсовой работе базисными функциями.
В этом случае, подставляя (1.5) в выражение (1.1) и выполняя дифференцирование в соответствии с (1.4), получим систему уравнений относительно искомых Сk. Подставим выражение аппроксимирующей функции для m базисных функций
ϕ(x) = С1 ϕ1(x) + С2 ϕ2(x) + … + Сm ϕm(x).
в формулу критерия аппроксимации (1.1).
Получим
 (1.6) Применим операцию дифференцирования (1.4) к параметру С1:
(1.6) Применим операцию дифференцирования (1.4) к параметру С1:
и, выполняя необходимые алгебраические преобразования, получим уравнение
 =
= 
Аналогичные уравнения можно получить, применяя описанные выше действия по отношению к переменным С2, …, Сm. Эти уравнения образуют систему нормальных уравнений


 (1.7)
(1.7)
где коэффициенты akl и величины bk (k, l = 1, 2, …, m) определяются выражениями

 (1.8)
(1.8)
Уравнения (1.7) представляют собой систему линейных алгебраических уравнений, основные методы решения которых описываются в разделах 2 и 3. Систему m линейных уравнений вида (1.7) можно записать посредством матричных обозначений в следующем виде:
A × C = B, где
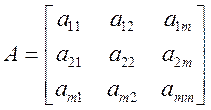 ,
,  ,
, 
(1.9)
РУЧНОЙ СЧЁТ