Абсолютная и относительная погрешность вычислений

Абсолютная погрешность вычислений находится по формуле:

Знак модуля показывает, что нам без разницы, какое значение больше, а какое меньше. Важно, насколько далеко приближенный результат отклонился от точного значения в ту или иную сторону.

Относительная погрешность вычислений находится по формуле:
, или, то же самое:

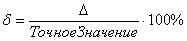
Относительная погрешность показывает, на сколько процентов приближенный результат отклонился от точного значения. Существует версия формулы и без домножения на 100%, но на практике я почти всегда вижу вышеприведенный вариант с процентами.

После короткой справки вернемся к нашей задаче, в которой мы вычислили приближенное значение функции с помощью дифференциала.

Вычислим точное значение функции с помощью микрокалькулятора:
, строго говоря, значение всё равно приближенное, но мы будем считать его точным. Такие уж задачи встречаются.

Вычислим абсолютную погрешность:

Вычислим относительную погрешность:
, получены тысячные доли процента, таким образом, дифференциал обеспечил просто отличное приближение.

Ответ: , абсолютная погрешность вычислений 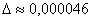, относительная погрешность вычислений

Следующий пример для самостоятельного решения:

Пример 4

Вычислить приближенно с помощью дифференциала значение функции в точке . Вычислить более точное значение функции в данной точке, оценить абсолютную и относительную погрешность вычислений.

Примерный образец чистового оформления и ответ в конце урока.

Многие обратили внимание, что во всех рассмотренных примерах фигурируют корни. Это не случайно, в большинстве случаев в рассматриваемой задаче действительно предлагаются функции с корнями.

Но для страждущих читателей я раскопал небольшой пример с арксинусом:

Пример 5

Вычислить приближенно с помощью дифференциала значение функции 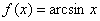в точке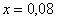

Этот коротенький, но познавательный пример тоже для самостоятельного решения. А я немного отдохнул, чтобы с новыми силами рассмотреть особое задание:

Пример 6

Вычислить приближенно с помощью дифференциала , результат округлить до двух знаков после запятой.

Решение: Что нового в задании? По условию требуется округлить результат до двух знаков после запятой. Но дело не в этом, школьная задача округления, думаю, не представляет для вас сложностей. Дело в том, что у нас дан тангенс с аргументом, который выражен в градусах. Что делать, когда вам предлагается для решения тригонометрическая функция с градусами? Например, и т. д.

Алгоритм решения принципиально сохраняется, то есть необходимо, как и в предыдущих примерах, применить формулу

Записываем очевидную функцию

Значение нужно представить в виде 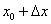. Серьёзную помощь окажет таблица значений тригонометрических функций. Кстати, кто её не распечатал, рекомендую это сделать, поскольку заглядывать туда придется на протяжении всего курса изучения высшей математики.

Анализируя таблицу, замечаем «хорошее» значение тангенса, которое близко располагается к 47 градусам:

Таким образом: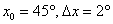

После предварительного анализа градусы необходимо перевести в радианы. Так, и только так!

В данном примере непосредственно из тригонометрической таблицы можно выяснить, что . По формуле перевода градусов в радианы: 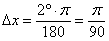(формулы можно найти в той же таблице).

Дальнейшее шаблонно:

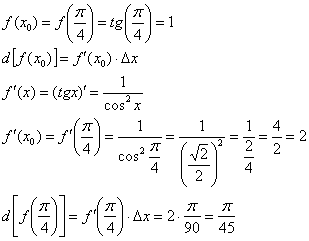
Таким образом: 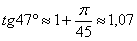(при вычислениях используем значение ). Результат, как и требовалось по условию, округлён до двух знаков после запятой.

Ответ: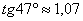

Пример 7

Вычислить приближенно с помощью дифференциала , результат округлить до трёх знаков после запятой.

Это пример для самостоятельного решения. Полное решение и ответ в конце урока.

Как видите, ничего сложного, градусы переводим в радианы и придерживаемся обычного алгоритма решения.

Приближенные вычисления
с помощью полного дифференциала функции двух переменных

Всё будет очень и очень похоже, поэтому, если вы зашли на эту страницу именно этим заданием, то сначала рекомендую просмотреть хотя бы пару примеров предыдущего пункта.

Для изучения параграфа необходимо уметь находить частные производные второго порядка, куда ж без них. На вышеупомянутом уроке функцию двух переменных я обозначал через букву 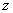. Применительно к рассматриваемому заданию удобнее использовать эквивалентное обозначение .

Как и для случая функции одной переменной, условие задачи может быть сформулировано по-разному, и я постараюсь рассмотреть все встречающиеся формулировки.

Пример 8

Вычислить приближенное значение функции 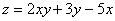в точке с помощью полного дифференциала, оценить абсолютную и относительную погрешность.

Решение: Как бы ни было записано условие, в самом решении для обозначения функции, повторюсь, лучше использовать не букву «зет», а .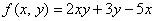

А вот и рабочая формула:

Перед нами фактически старшая сестра формулы предыдущего параграфа. Переменная только прибавилась. Да что говорить, сам алгоритм решения будет принципиально таким же!

По условию требуется найти приближенное значение функции в точке .

Число 3,04 представим в виде 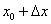. Колобок сам просится, чтобы его съели:
,

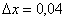
Число 3,95 представим в виде . Дошла очередь и до второй половины Колобка:
,

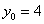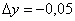
И не смотрите на всякие лисьи хитрости, Колобок есть – надо его съесть.

Вычислим значение функции в точке :

Дифференциал функции в точке найдём по формуле:

Из формулы следует, что нужно найти частные производные первого порядка и вычислить их значения в точке .

Вычислим частные производные первого порядка в точке :

Полный дифференциал в точке :

Таким образом, по формуле приближенное значение функции в точке :

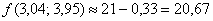
Вычислим точное значение функции в точке :

Вот это значение является абсолютно точным.

Погрешности рассчитываются по стандартным формулам, о которых уже шла речь в этой статье.

Абсолютная погрешность:

Относительная погрешность:

Ответ: 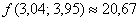, абсолютная погрешность: , относительная погрешность:

Пример 9

Это пример для самостоятельного решения. Кто остановится подробнее на данном примере, тот обратит внимание на то, что погрешности вычислений получились весьма и весьма заметными. Это произошло по следующей причине: в предложенной задаче достаточно велики приращения аргументов: . Общая закономерность такова – чем больше эти приращения по абсолютной величине, тем ниже точность вычислений. Так, например, для похожей точки 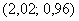приращения будут небольшими: 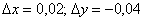, и точность приближенных вычислений получится очень высокой.

Данная особенность справедлива и для случая функции одной переменной (первая часть урока).

Пример 10

С помощью полного дифференциала функции двух переменных вычислить приближенно значение данного выражения. Вычислить это же выражение с помощью микрокалькулятора. Оценить в процентах относительную погрешность вычислений.

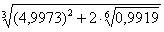
Решение: Вычислим данное выражение приближенно с помощью полного дифференциала функции двух переменных:

Отличие от Примеров 8-9 состоит в том, что нам сначала необходимо составить функцию двух переменных: . Как составлена функция, думаю, всем интуитивно понятно.

Значение 4,9973 близко к «пятерке», поэтому: , .
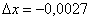Значение 0,9919 близко к «единице», следовательно, полагаем: , .

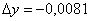Вычислим значение функции в точке :

Дифференциал в точке найдем по формуле:

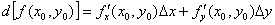
Для этого вычислим частные производные первого порядка в точке .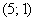

Производные здесь не самые простые, и следует быть аккуратным:
;

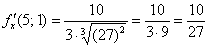
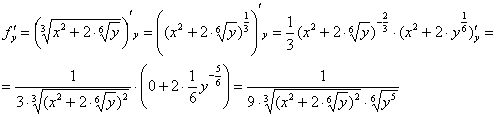
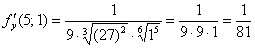Полный дифференциал в точке :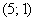

Таким образом, приближенное значение данного выражения:

Вычислим более точное значение с помощью микрокалькулятора: 2,998899527

Найдем относительную погрешность вычислений:

Ответ: ,

Как раз иллюстрация вышесказанному, в рассмотренной задаче приращения аргументов очень малы 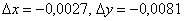, и погрешность получилась фантастически мизерной.

Пример 11

Это пример для самостоятельного решения. Примерный образец чистового оформления в конце урока.

Как уже отмечалось, наиболее частный гость в данном типе заданий – это какие-нибудь корни. Но время от времени встречаются и другие функции. И заключительный простой пример для релаксации:

Пример 12

С помощью полного дифференциала функции двух переменных вычислить приближенно значение функции , если

Решения и ответы:

Пример 2:Решение:Используем формулу:
В данном случае: , ,

Таким образом:
Ответ:

Пример 4:Решение:Используем формулу:
В данном случае: , ,

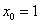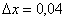
Таким образом:
Вычислим более точное значение функции с помощью микрокалькулятора:

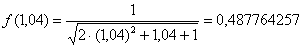
Абсолютная погрешность:

Относительная погрешность:

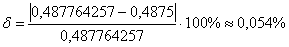
Ответ: , абсолютная погрешность вычислений 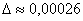, относительная погрешность вычислений

Пример 5:Решение:Используем формулу:
В данном случае: , ,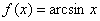

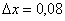
Таким образом:
Ответ: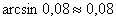

Пример 7:Решение:Используем формулу:
В данном случае: , ,

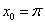Таким образом: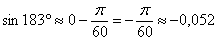
Ответ: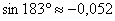

Пример 9:Решение: Используем формулу:
В данной задаче:
, , , , .

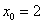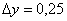Вычислим частные производные первого порядка в точке :

Полный дифференциал в точке :

Таким образом: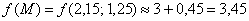
С помощью калькулятора вычислим точное значение функции в данной точке:

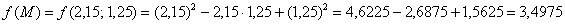
Абсолютная погрешность:

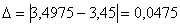
Относительная погрешность:

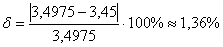
Ответ: 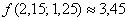, абсолютная погрешность: 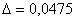, относительная погрешность:

Пример 11:Решение: С помощью полного дифференциала вычислим данное выражение приближенно:

В данной задаче:

,
,

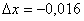
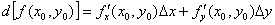
Вычислим частные производные первого порядка в точке :

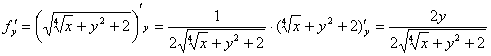
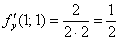
Полный дифференциал в точке :

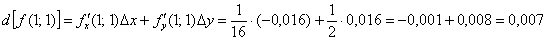
Таким образом, приближенное значение данного выражения:

Значение, вычисленное с помощью микрокалькулятора: 2,007045533
Найдем относительную погрешность вычислений:

Ответ: ,

Пример 12:Решение:Используем формулу: .
В данной задаче: , , , , .

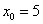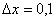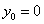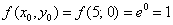
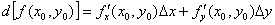
Вычислим частные производные первого порядка в точке :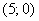

Полный дифференциал в точке :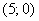

Таким образом:

Ответ:

⇐ Предыдущая 1 2 34