Главная | Обратная связь

Кинетические явления (явления переноса). Переносимая величина, уравнение процесса, коэффициент процесса

Таблица 16.1

Явление пере- носа	Переносимая величина	Уравнение процесса	Коэффициент процесса
Внутреннее трение (вяз- кость)	Количество движение (импульс)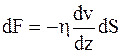
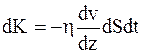
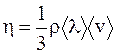
Теплопро- водность	Энергия (теплота)
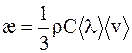
Диффузия	Масса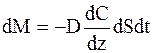

 

Лекция 17. Элементы механики сплошных сред

Общие свойства жидкостей и газов. Кинематическое описание движения жидкости. Идеальная и вязкая жидкости. Гидростатика несжимаемой жидкости. Стационарное движение идеальной жидкости. Уравнение Бернулли. Гидродинамика вязкой жидкости. Силы внутреннего трения. Коэффициент вязкости. Стационарное течение вязкой жидкости. Уравнение неразрывности. Формула Пуазейля. Формула Стокса. Кинематика и динамика газов. Идеально упругое тело. Упругие деформации и напряжения. Закон Гука. Пластические деформации. Предел прочности.

Строение жидкостей

Теорию жидкого состояния разработал советский физик-теоретик Яков Ильич Френкель. Трудность создания надежной теории жидкого состояния вызвана тем, что по своему строению и свойствам жидкости занимают промежуточное положение между газами и твердыми телами. Если учесть, что газы, жидкости и твердые тела, с точки зрения молекулярных представлений, состоят из молекул и атомов, представляют агрегатные состояния вещества, то между ними нет существенных различий: всякое вещество в зависимости от параметров состояния может находиться в любом из агрегатных состояний.

Однако между газами, жидкостями и твердыми телами имеются существенное различие, которое состоит в том, что газы занимают весь предоставленный ему объем, тогда как жидкости и твердые тела, занимают лишь часть его, что обусловлено различием в характере теплового движения и взаимодействием их молекул.

Молекулы газов почти не связаны между собой межмолекулярными силами. Их средняя кинетическая энергия теплового движения гораздо больше средней потенциальной энергии, обусловленной силами взаимодействия между ними. Поэтому молекулы газа совершают относительно большие пробеги, "разлетаясь" друг от друга на расстояния, зависящие от размеров сосуда, занимая весь его объем. Данное утверждение подтверждается довольно быстро протекающей в газах диффузией.

В жидкостях и твердых телах силы взаимодействия между молекулами (атомами, ионами) играют существенную роль, удерживают их на определенных расстояниях. Средняя потенциальная энергия, обусловленная данными силами, больше средней кинетической энергии теплового движения. Величина ее оказывается недостаточной для преодоления сил притяжения, поэтому молекулы жидкостей и твердых тел не совершают больших пробегов, совершают колебательные движения относительно некоторого положения равновесия. Иногда, вследствие благоприятной комбинации столкновений, молекула жидкости может перейти на новое местоположение, на расстояние, сравнимое с размерами самой молекулы. Это подтверждается значительно медленнее протекающей в них диффузией.

Рентгеноструктурные исследования жидкостей показали, что их внутреннее строение имеет много общего со строением твердых тел, состоящих из большого числа, малых по размеру, кристаллов с беспорядочным расположением осей. Однако "элементарные кристаллики", непрерывно образующиеся и разрушающиеся внутри жидкости, имеют незначительные размеры и могут перемещаться в пределах объема, занимающего жидкостью. В расположении молекул жидкости наблюдается так называемый ближний порядок, т.е. по отношению к любой молекуле расположение ближайших к ней соседей является упорядоченным. Однако, по мере удаления от нее, расположение других молекул по отношению к данной становится менее упорядоченным, и довольно быстро порядок в расположении молекул полностью исчезает.

Связь между основными параметрами состояния (объемом, давлением и температурой) у жидкостей гораздо сложнее, чем у газов. Наиболее универсальные закономерности в них устанавливаются, с определенной степенью точности уравнением состояния - уравнением Ван-дер-Ваальса, в котором поправки "а" и "в" определяются типом жидкости.

Наиболее простыми свойствами обладают жидкости, состоящие из сферически симметричных молекул, между которыми действуют силы Ван дер Ваальса, не имеющие какого-либо преимущественного направления. Такие жидкости называются простыми (сжиженные неон, аргон, и другие благородные газы, чистые жидкие металлы и т. д.).

Примером непростой жидкости является вода. Силы взаимодействия между молекулами воды имеют резко выраженный направленный характер. Взаимодействие между молекулами жидкостей, состоящих из многоатомных молекул, носит еще более сложный характер. Структура таких жидкостей еще мало изучена.

Если предположить, что среднее время, в течение которого молекула жидкости совершает колебательное движение относительно данного положения равновесия, время "оседлой" жизни (t_o), которое зависит от природы жидкости, а время одного колебания относительно данного положения равновесия t, то между t_o и t существует связь

(17.1)

где U - "потенциальный барьер", численно равный разности энергий молекулы в двух возможных областях колебаний молекулы ("потенциальный барьер", разделяющий две возможные области колебаний молекулы);

Т - температура жидкости;

k - постоянная Больцмана.

Из данного выражения следует, что с ростом температуры время оседлой жизни молекулы уменьшается, т.е. молекулы становятся более подвижными.

В современной теории жидкости многие их свойства описываются с помощью функций распределения, которые определяют вероятность нахождения некоторой молекулы жидкости в какой-либо точке ее объема. Эта вероятность зависит от того, в какой точке объема находится другая молекула этой же жидкости. Такая вероятностная связь описывается функцией распределения F(r₁, r₂).

В случае простой жидкости функция распределения зависит только от расстояния r = |r₂ – r₁| между молекулами и называется радиальной функцией распределения F(r).

С помощью радиальной функции распределения можно определить число молекул жидкости в некотором сферическом слое толщиной dr на расстоянии r от произвольно выбранной молекулы

(17.2)

где n_o = N/V - число молекул в единице объема жидкости.

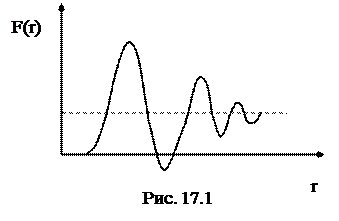График функции распределения F(r) имеет несколько достаточно выраженных максимумов (£3) (рис.17.1).

Область вблизи начала координат, F(r) = 0, соответствует эффективному диаметру молекулы. В этой области проявляется взаимная непроницаемость молекул. Области максимумов соответствуют наиболее предпочтительным взаимным расстояниям от данной молекулы до ее первых, вторых и т.д. соседей. При еще больших расстояниях r, F(r) » 1, т.е. все взаимные расположения удаленных частиц оказываются равновероятными. Горизонтальная прямая соответствует газу. Таким образом, функция распределения достаточно наглядно описывает ближний порядок в жидкостях.