 |
|
Свойства жидкостей (вязкость, текучесть, сжимаемость и тепловое расширение)
На рис.17.2 поясняется особенность строения жидкостей. Чтобы молекуле оказаться на новом месте, ей приходиться «протиснуться» между двумя соседями, образующими «узкий коридор». Френкель предложил математическую интерпретацию такого перехода: вероятность того, что молекула перейдет в новое положение равновесия зависит от соотношения тепловой энергии kT и высоты потенциального барьера ∆Е, который приходится преодолеть, чтобы оказаться в свобод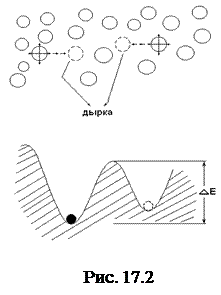 
ном месте. Вероятность перехода w по Френкелю пропорциональна экспоненте в степени -∆Е/kT
~ 
. (17.3)
При этом время оседлой жизни обратно пропорционально w.
Одним из свойств жидкостей является вязкость, которая определяется их молекулярным составом и строением. Она аналогична внутреннему трению в газах и относится к явлениям переноса в жидкой среде. Оценивается вязкость жидкостей по коэффициенту вязкости, который определяет величину силы трения между соседними ее слоями
, (17.4)
где dv/dz - градиент скорости в направлении z;
S – поверхность соприкасающихся слоев жидкости.
Физический смысл коэффициента вязкости - он численно равен силе внутреннего трения, возникающей между двумя слоями жидкости при S = 1 и градиенте скорости равном единице.
В отличие от коэффициента вязкости в газах, который уменьшается с уменьшением температуры T, коэффициент вязкости жидкостей возрастает с уменьшением их температуры, что вытекает из теории Френкеля
(17.5)
где U - энергия необходимая для перехода молекулы жидкости из одного равновесного состояния в другое.
Таким образом, с повышением температуры жидкости ее вязкость убывает по экспоненте. Этот вывод теории хорошо подтверждается на опыте. Противоположный характер температурной зависимости вязкости газов и жидкостей обусловлен принципиальным различием механизмов вязкости. В газах вязкость объясняется переносом импульса частицами из слоя в слой за счет хаотического теплового движения частиц. При этом интенсивность переноса импульса увеличивается с температурой. В жидкостях вязкость обусловлена преодолением потенциального барьера молекулой при переходе в новое положение равновесия (дырку), которое осуществляется тем легче, чем больше тепловая энергия молекулы kT и чем ниже высота барьера ∆Е. С уменьшением Т переход молекулы в соседнюю дырку затрудняется, вязкость возрастает.
Текучесть жидкостей свойство обратное вязкости, которое обусловлено той свободой движения молекул в объеме, которая еще допускается силами сцепления между ними.
Известно, что молекулы жидкости не связаны между собой "жестко"; каждая молекула, совершая беспорядочное движение, может изменять свое местоположение относительно "соседей" и стечением времени перемещается в объеме сосуда. Если время действия внешних сил, приложенных к жидкости, меньше, чем время "оседлой жизни" молекулы, то для того, чтобы вызвать деформацию жидкости, т.е. сместить одни ее молекулы относительно других, необходимо преодолеть упругие силы, действующие между ними. Чем больше время пребывания молекулы в "одном месте", время "оседлости", тем больше вязкость и меньше текучесть жидкости.
Сжимаемость. Так как молекулы в жидкостях находятся значительно ближе друг другу, чем в газах, то силы их межмолекулярного взаимодействия, вандерваальсовы силы, играют значительную роль, а, следовательно, внутреннее давление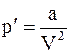 
в жидкостях очень велико.
На величину внутреннего давления в жидкостях, кроме того, влияет удельный объем, который в тысячи раз меньше, чем в газах.
Пренебрегая внешним давлением p в уравнении Ван дер Ваальса, уравнение состояния жидкости можно записать так
. (17.6)
Значительной величиной молекулярного (внутреннего) давления объясняется малая сжимаемость жидкостей. Коэффициент сжимаемости жидкостей K определяется соотношением
(17.7)
где dV - уменьшение первоначального объема жидкости V при увеличении давления на dp.
Коэффициент сжимаемости жидкостей зависит от давления и температуры: с увеличением давления он уменьшается, а с повышением температуры - увеличивается. Уменьшение коэффициента сжимаемости с ростом давления обусловлено тем, что по мере сближения молекул возрастают силы отталкивания между ними. Его увеличение с ростом температуры связано с увеличением расстояния между молекулами, вследствие увеличения объема жидкости.
Молекула, находящаяся внутри некоторого большого объема жидкости подвергается воздействию со стороны других молекул, притягивающих ее вследствие наличия вандерваальсовых сил. Область, в которой расположены эти взаимодействующие молекулы, можно представить как сферу, в центре которой находится рассматриваемая молекула. Такая сфера носит название сферы действия молекулярных сил (R ~ 10-9 м).
Так как молекулы в жидкостях расположены с равномерной плотностью, то равнодействующая молекулярных сил, действующих на рассматриваемую молекулу равна нулю. Поэтому перемещение молекул внутри жидкости хаотическое (тепловое), а не под действием сил Ван дер Ваальса.
Экспериментально было установлено, что с повышением температуры объем жидкости увеличивается согласно уравнению
, (17.8)
где a - коэффициент объемного расширения, который определяется соотношением 
.
Коэффициент объемного расширения жидкостей сильно зависит от температуры и давления. С увеличением температуры он возрастает, а с увеличением давления - уменьшается.
Коэффициенты сжимаемости и объемного расширения жидкостей связаны между собой соотношением
. (17.9)
Согласно соотношению (17.9) изменение давления жидкости с изменением температуры на 1 градус, при постоянном объеме, равно отношению коэффициента объемного расширения к коэффициенту сжимаемости. Поэтому небольшой перегрев жидкости в закрытых сосудах приводит к резкому возрастанию давления в них (для ртути это отношение равно ~45×105 Па/град).
Как было сказано выше, повышение температуры жидкости ведет к увеличению объема. Аномалией обладает только вода, для которой в области температур от 0 С до 4 С, повышение температуры приводит к уменьшению ее объема. Это объясняется тем, что молекулы воды образуют тесно связанные группы. В результате, наряду с молекулами воды типа H2O, в ней имеются молекулы типа (H2O)2, (H2O)3, удельный объем которых различен. С изменением температуры соотношение концентраций этих молекул изменяется, изменяется объем жидкости, достигая минимума при 4 С.
17.3. Поверхностное натяжение. Энергия поверхностного слоя жидкости
Силы взаимодействия между молекулами жидкости быстро убывают и действуют только внутри сферы молекулярного действия с центром в данной молекуле. При этом если молекула находится внутри жидкости, то результирующая сил молекулярного взаимодействия равна нулю. Это не относится к молекулам, находящимся у поверхности жидкости, в ее поверхностном слое. На молекулы поверхностного слоя действует сила направленная внутрь жидкости, перпендикулярно ее поверхности Объясняется это тем, что концентрация молекул жидкости над ее поверхностью (в паре или газе, с которым граничит жидкость) мала (рис.17.3).
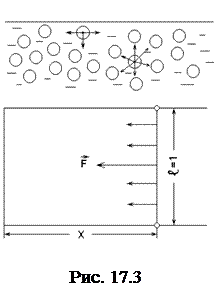Эта равнодействующая стремится втянуть внутрь данную молекулу во внутренние слои жидкости. Следовательно, весь поверхностный слой жидкости находится в особом состоянии. Он оказывает на жидкость некоторое давление. В соответствии с этим молекулы жидкости в поверхностном слое обладают дополнительной потенциальной энергией.
Перемещение молекулы из поверхностного слоя внутрь жидкости сопровождается совершением работы, при этом потенциальная энергия молекул поверхностного слоя уменьшается, переходит в кинетическую энергию этих молекул. Переход молекулы из глубины жидкости в поверхностный слой требует совершения работы по преодолению результирующей силы. Эта работа может совершаться за счет дополнительной энергии за счет ее кинетической энергии. Потенциальная энергия молекулы, перешедшей в поверхностный слой, увеличивается. С течением времени, при неизменных внешних условиях, устанавливается равновесие (число молекул, покинувших поверхностный слой, будет равно числу молекул вновь оказавшихся в этом слое). Число молекул в поверхностном слое будет неизменным.
Кроме сил, действующих на молекулы поверхностного слоя в перпендикулярном направлении к поверхности, на них действуют силы в горизонтальном направлении (по касательной к поверхности жидкости). Они вызывают стремление жидкости сократить (уменьшить) свою поверхность. Эти силы получили название сил поверхностного натяжения. Следовательно, силы поверхностного натяжения направлены по касательной к поверхности жидкости, перпендикулярно к участку контура, охватывающего поверхность жидкости.
Изменение внешних условий может изменить поверхность жидкости, в результате нарушается равновесие, и некоторое количество молекул может перейти в поверхностный слой. В этом случае будет совершаться работа dA пропорциональная изменению поверхности жидкости на dS
, (17.10)
где "минус" показывает, что увеличение поверхности жидкости сопровождается совершением работы;
s - коэффициент поверхностного натяжения, который характеризует свойства поверхности жидкости и показывает, какую работу необходимо совершить, чтобы увеличить поверхность жидкости на единицу поверхности.
Работа по изменению поверхности жидкости может совершаться либо за счет изменения потенциальной энергии поверхностного слоя жидкости, (поверхностной энергии жидкости dWps), либо внешними силами. При этом 
, но тогда
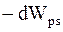
или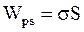 
. (17.11)
Потенциальная энергия поверхностного слоя жидкости Wps является составной частью внутренней энергии жидкости и ее свободной энергии.
Известно, что при неизменных внешних условиях, в частности при постоянной температуре, любая термодинамическая система стремится к состоянию с свободной минимальной энергией. А так как Wps ~ S, то, следовательно, Wps к минимальному значению, при минимальном значении поверхности S. Таким образом, при постоянной температуре жидкость стремится к такому состоянию, при котором ее поверхность минимальна. Данное утверждение позволяет предсказать, как будет вести себя жидкость в тех или иных условиях.
Предположим, что поверхностный слой жидкости занимает некоторую поверхность. Этот слой стремится уменьшить свою поверхность. Чтобы система находилась в равновесии, к границе слоя необходимо приложить силу, численно равную силе поверхностного натяжения F (рис.17.3).
Если под действием этой силы граница поверхностного слоя сместится на dx, то будет совершена работа 
.
Эта работа
(17.12)
тогда
откуда
a 
. (17.13)
Следовательно, коэффициент поверхностного натяжения, численно равен силе поверхностного натяжения, которая стремится изменить длину (величину) контура, охватывающего поверхность жидкости, на единицу.
Силами поверхностного натяжения определяется форма капель жидкости. Так как обычно жидкость находится в поле земного тяготения, то ее капли принимают форму, соответствующую минимальной сумме поверхностной энергии и потенциальной энергии в поле тяготения в зависимости от соотношения этих энергий. У капель жидкости, обладающих достаточным объемом, форма типа эллипсоида. По мере уменьшения размеров капли поверхностная энергия начинает играть существенную роль, т.к. объем и масса капли уменьшаются пропорционально кубу, а ее поверхность - квадрату радиуса. Поэтому очень малые капли принимают шарообразную форму. В условиях невесомости жидкость принимает сферическую форму при любом объеме.
Установить зависимость коэффициента поверхностного натяжения от температуры можно, применив к растяжению жидкой пленки первое начало термодинамики.
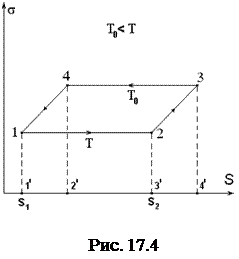Предположим, что пленка состоит из чистой жидкости, (хотя такая пленка неустойчива) и в ней совершается некоторый замкнутый цикл, состоящий из изотермического и адиабатического расширений и таких же процессов сжатия. Пусть в начальном состоянии пленка находится в некотором состоянии "1" и характеризуется температурой T. Сообщив ей некоторое количество тепла dQ, можно изотермически перевести (растянуть) ее в состояние "2". Произойдет изменение площади пленки на 
, за счет совершенной работы (рис. 17.4). При этом
. (17.14)
Поверхностное натяжение в этом случае не изменится.
Если из состояния "2" пленку адиабатически перевести в состояние "3" (растянуть), то за счет работы внешних сил, температура понизится на dT, что приведет к изменению коэффициента поверхностного натяжения на ds.
При изотермическом сокращении пленки, она перейдет в состояние "4", а при адиабатическом - вернется в состояние "1".
Работа такого цикла равна разности работ при расширении и сжатии. Можно показать, что она в этом случае будет равна
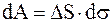. (17.15)
Если учесть, что вначале пленкой было получено dQ теплоты, то коэффициент полезного действия цикла
, (17.16)
где "минус" указывает на то, что при сокращении пленки выделяется некоторое количество тепла. Тогда
(17.17)
где r = dQ/DS - количество тепла, затраченное на изменение пленки на единицу.
Таким образом, с повышением температуры величина коэффициента поверхностного натяжения уменьшается.
Подобно упругой пленке поверхностный слой жидкости стремится принять форму плоскости. Поэтому в изогнутом слое жидкости появляются силы, создающие дополнительное давление, увеличивающее или уменьшающее молекулярное давление. С учетом данного утверждения полное молекулярное давление будет равно
, (17.18)
где po - молекулярное давление жидкости с плоской поверхностью;
Dp - дополнительное давление, возникающее за счет кривизны поверхности;
"плюс" - соответствует выпуклой поверхности;
"минус" – соответствует вогнутой поверхности.
Поверхностное натяжение жидкости обуславливает дополнительное давление в жидкости, величина которого зависит от радиуса кривизны поверхности и коэффициента поверхностного натяжения. Получим формулу для расчета дополнительного давления под искривленной поверхностью жидкости (твердого тела), называемую формулой Лапласа.
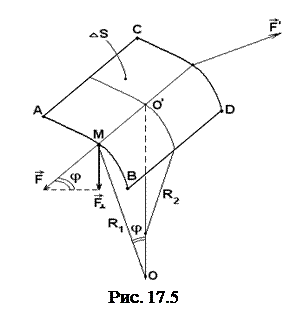
Будем считать, что кривизна элемента поверхности капли в двух взаимно перпендикулярных направлениях различна и определяется радиусами кривизны R1 и R2, как показано на рисунке 17.5.
Пусть площадь элемента поверхности равна ∆S. Вычислим силы поверхностного натяжения, приложенные к линиям "АВ" и "СД", которыми ограничен этот элемент поверхности F и F'. Составляющие этих сил направлены к центру кривизны и обуславливают дополнительное давление. Эти составляющие, перпендикулярны к ∆S и направлены параллельно радиусу кривизны. Если поверхность плоская, то нормальной составляющей силы нет, дополнительного давления также нет. (Вторая составляющая F|| на давление влияния не оказывает.) Итак, имеем:
(17.19)
Сила 
имеет такую же составляющую
; 
(17.20)
То же получим и для участков "АС" и "ВД" (только 
)
; 
(17.21)
; 
(17.22)
Сложив все четыре компонента, будем иметь
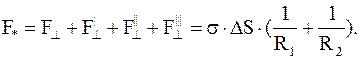(17.23)
Откуда для дополнительного давления находим
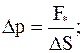
(17.24)
Полученное соотношение (17.24) называют формулой Лапласа. Из формулы Лапласа вытекает:
1) при R1 = R2 = R,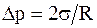 
, что справедливо для сферической поверхности;
2) при R2® ¥,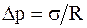 
, что справедливо для цилиндрической поверхности;
3) силы, создающие дополнительное давление, всегда направлены к центру кривизны поверхности жидкости. В случае выпуклой поверхности, радиус кривизны R положителен, следовательно, дополнительное давление увеличивает молекулярное давление. В случае вогнутой поверхности, радиус кривизны R отрицателен, дополнительное давление уменьшает молекулярное давление.
Надо отметить, что полученный вывод справедлив для капли, которая полностью заполнена жидкостью, или для пузырька внутри жидкости.
Если имеется пузырек, например мыльный, то давление, которое оказывает поверхность пузырька на заключенный на него газ, вдвое больше. Это объясняется тем, что у такого пузырька две поверхности: наружная и внутренняя, каждая из которых создает почти одинаковые дополнительные давления. В этом случае:
а) для сферической поверхности
; (17.25)
б) для цилиндрической поверхности
. (17.26)