 |
|
Правила виконання контрольної роботи
МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ
ОДЕСЬКИЙ ТЕХНІЧНИЙ КОЛЕДЖ
ОДЕСЬКОЇ НАЦІОНАЛЬНОЇ АКАДЕМІЇ ХАРЧОВИХ ТЕХНОЛОГІЙ
НАВЧАЛЬНО-ПРАКТИЧНИЙ КОМПЛЕКС
З предмету
“ВИЩА МАТЕМАТИКА”
для студентів заочної форми навчання

Одеса - 2012
Навчально-практичний комплекс дисципліни «Вища математика» для студентів заочної форми навчання (Частина 1)/ Уклад.:Т.В.Качан. – Одеса, Одеський технічний коледж, 2012 р.
Укладач – Т.В.Качан викладач математики Одеського технічного коледжу
Рецензент - О.П.Свєтной, к.ф.-м.н., доцент, зав. кафедрою методики викладання математики ПДПУ ім. К.Д.Ушинського
Навчально-практичний комплекс дисципліни (частина 1) містить методичні рекомендації, навчально-тематичний план, програму вивчення курсу «Вища математика» для студентів економічних та технічних спеціальностей заочної форми навчання, питання для самоперевірки, питання для перевірки знань в процесі підсумкового контролю, контрольні завдання з прикладами вирішення типових задач та перелік рекомендованої літератури.

МІНІСТЕРСТВО ОСВІТИ І НАУКИ, МОЛОДІ ТА СПОРТУ УКРАЇНИ
ОДЕСЬКИЙ ТЕХНІЧНИЙ КОЛЕДЖ
ОДЕСЬКОЇ НАЦІОНАЛЬНОЇ АКАДЕМІЇ ХАРЧОВИХ ТЕХНОЛОГІЙ
| ЗАТВЕРДЖУЮ: Заст. директора з НР __________ В.І. Уманська «___» ____________ 2012 р. |
НАВЧАЛЬНО-ПРАКТИЧНИЙ КОМПЛЕКС
З предмету
“ВИЩА МАТЕМАТИКА”
для студентів заочної форми навчання спеціальностей
5.03051001«Товарознавство та комерційна діяльність» ,
5.05160203 «Моделювання та конструювання
виробів народного вжитку»
5.05170104 «Виробництво хліба, кондитерських, макаронних виробів і харчо концентратів»
5.05060403«Монтаж і обслуговування холодильно-компресорних машин та установок»
РОЗГЛЯНУТО
На засіданні циклової комісії
Фізико-математичних дисциплін
Протокол № ______________
Від «____» _________ 2012 р.
Голова циклової комісії _____________ Качан Т.В.
Одеса - 2012
МЕТОДИЧНІ РЕКОМЕНДАЦІЇ
Навчально-практичний комплекс пропонується для вивчення курсу “Вища математика” студентами заочної форми навчання економічних та технічних спеціальностей вищих навчальних закладів І-ІІ рівня акредитації.
Розробка містить п’ять розділів – лінійна алгебра, векторна алгебра та аналітична геометрія, комплексні числа, вступ до математичного аналізу, диференціальне числення функції однієї змінної, які є базовим теоретичним та обчислювальним інструментом для подальшого вивчення студентами таких дисциплін, як економічна статистика, програмування тощо.
Викладання курсу вищої математики має своєю головною метою навчити студентів користуватися математичним апаратом при розв’язанні теоретичних і практичних задач спецпредметів, самостійно вивчати учбову літературу з математики та її застосувань, розвивати логічне мислення, виробити навички математичного дослідження прикладних питань.
До кожного розділу, який буде винесено на домашню контрольну роботу наведені завдання для самостійної роботи студентів, приклади вирішення типових задач курсу, а також контрольні питання, що увійшли до екзаменаційних білетів.
В процесі вивчення дисципліни передбачається систематична самостійна робота студентів з наведеною нижче рекомендованою літературою, а також робота під керівництвом викладача (лекційні, практичні аудиторні заняття, консультації).
Без належного засвоєння теоретичного матеріалу неможливе правильне, усвідомлене розв’язання практичних завдань з курсу.
Студенти, які правильно виконали контрольну роботу, подану нижче, будуть допущені до підсумкової перевірки знань, передбаченої у вигляді іспиту.
НАВЧАЛЬНО-ТЕМАТИЧНИЙ ПЛАН
| № п/п | Назва розділів і тем |
| 1. 2. 3. 4. 5. | РОЗДІЛ 1. Лінійна алгебра. |
| Загальні поняття про систему лінійних рівнянь. Матриці. Види матриць. Дії з матрицями. Визначники матриць. Обернена матриця. Матричні рівняння. Способи розв’язання систем лінійних рівнянь. | |
| РОЗДІЛ 2. Векторна алгебра та аналітична геометрія. | |
| 6 7 8 | Вектори та координати. Пряма лінія на площині. Криві другого порядку. |
| 9. 10. 11. 12. | РОЗДІЛ 3. Комплексні числа. |
| Комплексні числа та операції над ними. Розв’язок квадратних рівнянь з дійсними коефіцієнтами. Геометрична інтерпретація та тригонометрична форма комплексного числа. Показникова форма комплексного числа. | |
| 13. 14. 15. 16. | РОЗДІЛ 4. Вступ до математичного аналізу. |
| Функції однієї змінної та способи їх задання. Границя числової послідовності. Границя функції. Неперервність функції в точці і на відрізку. | |
| 17. 18. 19. 20. 21. | РОЗДІЛ 5. Диференціальне числення функцій однієї змінної. |
| Похідна функції. Знаходження похідних першого порядку. Похідні вищих порядків. Диференціал функції однієї змінної. Застосування похідної. Побудова графіка функції. |
ПРОГРАМА ВИВЧЕННЯ ДИСЦИПЛІНИ “ВИЩА МАТЕМАТИКА”
Розділ 1. Лінійна алгебра.
Тема 1. Загальні поняття про систему лінійних рівнянь.
Система m лінійних алгебраїчних рівнянь з n невідомими. Невідомі змінні, коефіцієнти при невідомих, вільні члени системи. Розв’язок системи. Сумісні, несумісні, визначені, невизначені, однорідні, неоднорідні системи. Еквівалентні (рівносильні) системи, елементарні перетворення для систем.
Тема 2. Матриці, види матриць, дії з матрицями.
Поняття прямокутної матриці, основна та розширена матриці системи лінійних рівнянь. Елементи матриці, рядки і стовпчики матриці. Головна та побічна діагоналі матриці.
Квадратна, симетрична, діагональна, одинична матриці. Операція транспонування матриць. Рівність матриць.
Найпростіші дії з матрицями: додавання матриць одного розміру, добуток матриці на число, добуток двох матриць. Властивості дій з матрицями.
Тема 3. Визначники матриць.
Обчислення визначників 2-го, 3-го, n-го порядків. Мінор та алгебраїчне доповнення елемента матриці. Властивості визначників.
Тема 4. Обернена матриця, матричні рівняння.
Обернена матриця. Вироджені та невироджені матриці. Знаходження оберненої матриці. Матричні рівняння.
Тема 5. Способи розв’язання систем лінійних рівнянь.
Метод Крамера. Матричний метод (за допомогою оберненої матриці). Метод Гаусса.
Розділ 2. Векторна алгебра та аналітична геометрія.
Тема 6. Вектори та координати.
Скалярні та векторні величини. Лінійні операції над векторами. Скалярний добуток векторів.
Системи координат на площині та у просторі. Операції над векторами, що задані своїми координатами.
Відстань між двома точками. Ділення відрізка у даному відношенні.
Перетворення прямокутних координат.
Тема 7. Пряма лінія на площині.
Рівняння лінії на площині. Канонічне та параметричне рівняння прямої. Рівняння прямої, що проходить через задану точку перпендикулярно заданому вектору. Загальне рівняння прямої.
Інші форми рівняння прямої на площині. Дослідження взаємного розташування двох прямих. Обчислення кута між прямими.
Тема 8. Криві другого порядку.
Коло. Еліпс. Гіпербола. Парабола.
Розділ 3. Комплексні числа.
Тема 9. Комплексні числа та операції над ними.
Вступні зауваження відносно подальшого розповсюдження поняття числа. Визначення комплексних чисел. Додавання та множення комплексних чисел. Дійсні числа як частинний випадок комплексних. Алгебраїчна форма комплексного числа. Віднімання та ділення комплексних чисел.
Тема 10. Розв’язок квадратних рівнянь з дійсними коефіцієнтами.
Розв’язок квадратних рівнянь з дійсними коефіцієнтами. Формули та деякі окремі випадки.
Тема 11. Геометрична інтерпретація та тригонометрична форма комплексного числа.
Геометрична інтерпретація комплексних чисел. Геометричне зображення суми комплексних чисел. Геометричне зображення різниці комплексних чисел. Модуль комплексного числа. Аргумент комплексного числа. Тригонометрична форма комплексного числа. Дії над комплексними числами заданими у тригонометричній формі.
Тема 12. Показникова форма комплексного числа.
Формула Ейлера. Показникова форма комплексного числа. Дії над комплексними числами заданими у показниковій формі.
Розділ 4. Вступ до математичного аналізу.
Тема 13. Функції однієї змінної та способи їх задання.
Змінні та сталі величини. Визначення функції однієї змінної. Способи задання функції: табличний, графічний, аналітичний. Область визначення та область значень функції. Деякі властивості функцій. Обернена функція. Функція, що задана в неявному вигляді. Складна функція. Основні елементарні функції та їх графіки.
Тема 14. Границя числової послідовності.
Поняття числової послідовності. Границя числової послідовності, геометрична інтерпретація. Збіжні та розбіжні послідовності. Загальні властивості збіжних послідовностей: теорема про єдину границю, необхідна умова збіжності послідовностей.
Нескінченно мала величина та її властивості. Нескінченно велика величина. Зв’язок між нескінченно малою та нескінченно великою величинами.
Граничний перехід при арифметичних операціях. Теореми для знаходження границь послідовностей.
Тема 15. Границя функції.
Визначення границі функції. Правосторонні та лівосторонні границі функції. Теорема про існування границі функції. Розкриття невизначених виразів типу  ,
,  ,
,  для алгебраїчних функцій. Перша особлива границя. Число е. Друга особлива границя.
для алгебраїчних функцій. Перша особлива границя. Число е. Друга особлива границя.
Тема 16. Неперервність функції в точці і на відрізку.
Різні означення неперервності функції в точці. Властивості неперервних функцій. Теорема Коші. Теорема Вейерштраса. Класифікація точок розриву функції.
Розділ 5. Диференціальне числення функцій однієї змінної.
Тема 17. Похідна функції.
Означення похідної функції. Поняття диференційованої функції. Деякі задачі, що привели до поняття похідної (геометричний, механічний, економічний зміст похідної). Зв’язок між неперервністю та диференційованістю функції.
Тема 18. Знаходження похідних першого порядку.
Основні правила диференціювання. Таблиця похідних основних елементарних функцій. Похідна складної, неявної та оберненої функції.
Тема 19. Похідні вищих порядків.
Похідні вищих порядків, їх позначення та обчислення.
Тема 20. Диференціал функції однієї змінної.
Означення диференціала функції. Правила знаходження диференціала.
Тема 21. Застосування похідної. Побудова графіка функції.
Правило Лопіталя. Необхідні і достатні умови зростання, спадання, екстремуму функції. Найбільше та найменше значення функції на відрізку. Опуклість та угнутість графіка функції. Точки перегину. Асимптоти кривої. Загальна схема (алгоритм) дослідження функції та побудови її графіка.
Питання для самоперевірки.
1. Дати означення матриці та її розміру. Які існують різновиди матриць?
2. Які елементи утворюють головну та неголовну діагоналі матриці?
3. За якими правилами матрицю помножають на дійсне число, знаходять алгебраїчну суму матриць, добуток матриць?
4. Чи завжди добуток матриць має властивість комутативності?
5. За якими правилами обчислюють визначники 2, 3 та n-го порядків?
6. Як визначають і знаходять мінор та алгебраїчне доповнення елемента аij матриці А?
7. Сформулюйте властивості визначника.
8. Як визначають та позначають матрицю обернену до матриці А?
9. При яких умовах існує обернена матриця?
10. Які ви знаєте способи знаходження оберненої матриці?
11. Дайте визначення векторної та скалярної величини.
12. Які векторі називаються колінеарними та компланарними?
13. Сформулюйте правила додавання та віднімання векторів, множення вектора на число.
14. Що називають скалярним та векторним добутком векторів?
15. Запишіть формулу знаходження відстані між двома точками.
16. Запишіть формулу ділення відрізка у даному відношенні.
17. Що називається рівнянням лінії? Запишіть загальний вигляд канонічного та параметричного рівнянь прямої.
18. Який вигляд має рівняння прямої, що проходить через дану точку перпендикулярну даному вектору?
19. Запишіть загальне рівняння прямої. Які його частинні випадки вам відомі?
20. Запишіть формулу обчислення кута між прямими.
21. Як визначається лінії другого порядку? Що називається колом?
22. Запишіть канонічне рівняння еліпса, що таке ексцентриситет, фокуси еліпса?
23. Запишіть канонічне рівняння гіперболи, як визначається асимптоти гіперболи? Що таке ексцентриситет гіперболи?
24. Запишіть канонічне рівняння параболи? Що таке директриси?
25. Дайте визначення комплексного числа.
26. Як відбуваються дії над комплексними числами у алгебраїчній формі?
27. Дайте геометричну інтерпретацію комплексних чисел.
28. Як відбуваються дії над комплексними числами у тригонометричній формі?
29. Запишіть формулу Ейлера. Як відбуваються дії над комплексними числами у показниковій формі?
30. Які величини називають сталими, а які змінними?
31. Назвіть способи задання функцій.
32. Що таке область визначення та область значення функції?
33. Побудуйте ескізи графіків основних елементарних функцій.
34. Який існує зв’язок між нескінченно малою та нескінченно великою величиною?
35. Дати означення границі послідовності та границі функції.
36. Яка геометрична інтерпретація означення границі послідовності?
37. Назвіть деякі методи розкриття невизначеностей типу  ,
,  ,
,  для алгебраїчних функцій.
для алгебраїчних функцій.
38. Наведіть першу і другу особливі границі. Які їх наслідки?
39. Як визначають число е? Де його застосовують?
40. Поясніть, що таке приріст аргументу та функції?
41. Дайте визначення неперервності функції в точці і на відрізку.
42. Які існують розриви функції?
43. Чим відрізняється ліквідований розрив від неліквідованого?
44. Який геометричний, механічний, економічний зміст має похідна функція?
45. Дати визначення похідної функції.
46. Які існують правила знаходження похідної функції?
47. Як знайти похідну складної функції?
48. Як знайти похідну другого, третього та вищих порядків?
49. Що таке диференціал функції?
50. Які правила знаходження диференціала функції?
51. Сформулюйте правило Лопіталя.
52. Як знайти найбільше та найменше значення функції на відрізку?
53. Як визначити інтервали монотонності функції?
54. Як знайти максимум і мінімум функції?
55. Які необхідні та достатні умови існування екстремуму функції?
56. Назвіть необхідні і достатні умови точки перегину функції?
57. Які ознаки опуклості та угнутості кривої?
58. Яка пряма називається асимптотою кривої?
59. Наведіть загальну схему дослідження функції і побудови її графіка.
Питання для перевірки знань і умінь в процесі іспиту.
Розділ 1. Лінійна алгебра.
1. Загальні поняття про систему лінійних рівнянь.
2. Матриці, види матриць, дії з матрицями.
3. Визначники матриць. Властивості визначників. Обчислення визначників.
4. Обернена матриця, матричні рівняння.
5. Розв’язання систем лінійних рівнянь за правилом Крамера та за методом Гаусса.
Розділ 2. Векторна алгебра та аналітична геометрія.
1. Вектори, їх основні характеристики. Дії з векторами.
2. Лінійно залежні та лінійно-незалежні вектори. Розклад вектора за базисом.
3. Предмет аналітичної геометрії. Знаходження відстані між точками. Ділення відрізка у заданому відношенні.
4. Різновиди рівняння прямої на площині.
5. Паралельність, перпендикулярність прямих на площині, кут між прямими.
6. Криві лінії другого порядку. Рівняння кола.
7. Рівняння еліпса, гіперболи та параболи. Характеристики цих кривих.
Розділ 3. Комплексні числа.
1. Комплексні числа та операції над ними.
2. Розв’язок квадратних рівнянь з дійсними коефіцієнтами.
3. Геометрична інтерпретація та тригонометрична форма комплексного числа.
4. Показникова форма комплексного числа.
Розділ 4. Вступ до математичного аналізу.
1. Функції та способи їх задання. Властивості функцій.
2. Основні елементарні функції.
3. Нескінченно малі та нескінченно великі величини. Поняття границі функції. Чудові границі.
4. Неперервні функції та дії з ними. Класифікація розривів функції.
Розділ 5. Диференціальне числення функцій однієї змінної.
1. Похідна та диференціал. Знаходження похідних першого порядку.
2. Похідні вищих порядків Оптимізація та побудова графіка функції.
3. Приклади економічного застосування похідної.
КОНТРОЛЬНА РОБОТА
Правила виконання контрольної роботи
Контрольну роботу потрібно виконувати самостійно, дотримуючись наступних правил:
1. Контрольну роботу виконують в окремому зошиті чорнилом будь-якого кольору, окрім червоного, при цьому залишають поля для зауважень викладача.
2. На обкладинці зошита повинні бути розбірливо написані прізвище, ім’я, по батькові студента, номер учбової групи та шифр.
3. Номер варіанта контрольної роботи – це остання цифра шифру. В роботі повинні бути завдання тільки свого варіанту. Робота, яка містить завдання не свого варіанту, не перевіряється.
4. Перед розв’язанням завдання необхідно переписати його умову. Якщо завдання має загальне формулювання, то при переписуванні його умови потрібно загальні дані замінити конкретними зі свого варіанту.
5. Розв’язання задач повинно супроводжуватися необхідними поясненнями і малюнками.
6. Після отримання перевіреної роботи студент повинен у цьому ж зошиті виправити усі помилки, які були відмічені викладачем.
Завдання для контрольної роботи
Завдання 1.
Дані наведені в таблиці.
1. Виконати дії з матрицями: а)3А+2В; б) АВ; ВА; в) АС.
2. Обчислити визначник матриці А.
3. Знайти матрицю, обернену до матриці А.
4. Розв’язати матричне рівняння АХ=В.
5. Розв’язати систему рівнянь:
a) методом Крамера;
b) методом Гаусса;
c) матричним методом.
| Варіант | А | В | С | |

| 
| 
| 
| |

| 
| 
| 
| |

| 
| 
| 
| |

| 
| 
| 
| |

| 
| 
| 
| |

| 
| 
| 
| |
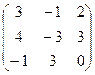
| 
| 
| 
| |

| 
| 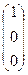
| 
| |

| 
| 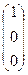
| 
| |

| 
| 
| 
|
Завдання 2.
1.
a) Дано  ,
,  ,
,  . Обчисліть
. Обчисліть  .
.
b) Скласти рівняння медіан трикутника з вершинами у точках А (-4;2), В (2;0) та С (2;-4).
c) Скласти канонічне рівняння гіперболи, якщо 2b=8, е=  .
.
2.
a) Вектори  і
і  перпендикулярні, причому
перпендикулярні, причому  ,
,  обчисліть
обчисліть  .
.
b) Визначити кутовий коефіцієнт і побудувати пряму: 2х-3у-6=0.
c) Скласти рівняння еліпса, фокуси якого лежать на осі ординат, якщо його більша вісь дорівнює 8, а відстань між фокусами 6.
3.
a) Обчисліть довжину вектора  , якщо
, якщо 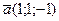 ,
,  .
.
b) Скласти рівняння прямої, що проходить через точку М(-2;4) паралельно осі абсцис.
c) Знати точку перетину еліпса  з прямою
з прямою 
4.
a) Дано:  ,
,  , (
, ( 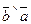 )
) 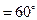 ,
,  . Обчисліть скалярний добуток (
. Обчисліть скалярний добуток (  ).(
).(  ).
).
b) Через точку перетину прямих 2х-5у-1=0 і х+4у-7=0 провести пряму, яка проходить через початок координат.
c) Знайти вершину, фокус, вісь та директрису параболи  .
.
5.
a) Обчисліть кут між векторами  та
та  , де
, де  - одиничні взаємно перпендикулярні вектори.
- одиничні взаємно перпендикулярні вектори.
b) Задано пряму у-2х-1=0 і точку М(-1;2). Написати рівняння прямої, що проходить через точку М перпендикулярно до заданої прямої.
c) Знайти довжини осей, координати фокусів та ексцентриситет еліпса  .
.
6.
a) Знайдіть кут між стороною АС і медіаною ВВ1 трикутника АВС, якщо А(3;5;0), В(0;-6;0) і С(3;1;0).
b) Задано пряму у-2х-1=0 і точку М(-1;2). Написати рівняння прямої, що проходить через точку М паралельно до заданої прямої.
c) Знайти координати центру та радіус кола:  .
.
7.
a) ТочкиА(3;1;8), В(4;7;1), С(3;5;-8) - вершини паралелограма АВСD. Знайдіть координати вершини D.
b) Задано пряму у-2х-1=0 і точку М(-1;2). Написати рівняння прямої, що проходить через точку М під кутом 450 до заданої прямої.
c) Знайти довжини осей, координати фокусів та ексцентриситет еліпса  .
.
8.
a) Від точки А відкладено вектор  Знайдіть координати точки В, якщо А(-1;5;0),
Знайдіть координати точки В, якщо А(-1;5;0),  (1;-3;0).
(1;-3;0).
b) Задано пряму 2у+1=0 і точку М(1;0). Написати рівняння прямої, що проходить через точку М перпендикулярно до заданої прямої.
c) Знайти відстань між центрами кіл:  та
та  .
.
9.
a) Дано точки А(8;-2;5), В(2;3;7), С(-3;9;4) i D(3;4;2) чи рівні вектори  і
і  ?
?
b) Задано пряму 2у+1=0 і точку М(1;0). Написати рівняння прямої, що проходить через точку М паралельно до заданої прямої.
c) Скласти рівняння еліпса, фокуси якого лежать на осі ординат, якщо відстань між фокусами дорівнює 6 та ексцентриситет 0,6.
10.
a) Дано вектори  , і
, і  . Знайдіть кут між векторами
. Знайдіть кут між векторами  і
і 
b) Знайти рівняння бісектриси внутрішнього кута С трикутника з вершинами А(0;0), В(3;-1), С(4;7).
c) Знайти рівняння асимптот та ексцентриситет гіперболи  .
.
Завдання 3. Знайти границі функцій.
1.
a) 
b) 
c) 
d) 
2.
a) 
b) 
c) 
d) 
3.
a) 
b) 
c) 
d) 
4.
a) 
b) 
c) 
d) 
5.
a) 
b) 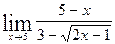
c) 
d) 
6.
a) 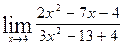
b) 
c) 
d) 
7.
a) 
b) 
c) 
d) 
8.
a) 
b) 
c) 
d) 
9.
a) 
b) 
c) 
d) 
10.
a) 
b) 
c) 
d) 
Завдання 4. Знайти похідні функцій.
1.
a) 
b) 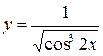
c) 
d) 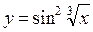 ;
;  .
.
2.
a) 
b) 
c) 
d)  ;
;  .
.
3.
a) 
b) 
c) 
d)  ;
; 
4.
a) 
b) 
c) 
d)  ;
; 
5.
a) 
b) 
c) 
d) 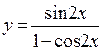 ;
; 
6.
a) 
b) 
c) 
d) 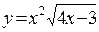 ;
; 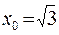 .
.
7.
a) 
b) 
c) 
d)  ;
; 
8.
a) 
b) 
c) 
d)  ;
; 
9.
a) 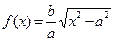
b) 
c) 
 ;
;  .
.
10.
a) 
b) 
c) 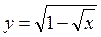
d)  ;
; 
Завдання 5.
Дослідити методами диференціального числення функцію і побудувати її графік.
1. 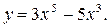
2. 
3. 
4. 
5. 
6. 
7. 
8. 
9. 
10. 