 |
|
Приклад розв’язання завдання 5.
Дослідити функцію 
та побудувати її графік.
Розв’язання:
а) Область визначення функції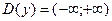 
, тобто функція існує при всіх значеннях.
б) Парність, періодичність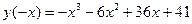 
, 
.
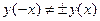Функція загального вигляду, ні парна, ні непарна, неперіодична.
в) Точки перетину з осями координат:
- з віссю ОХ: 
.
Легко перевірити, що 
є корінь рівняння, тому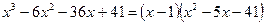 
.
Знайдемо дві інші точки перетину графіка з віссю ОХ: 
, 
.
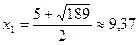Точки перетину графіка з віссю ОХ – А(1;0), В(-4,37;0), С(9,37;0), точка перетину графіка з віссю OY (х=0) – D(0;41).
г) Інтервали зростання та спадання функції, точки екстремуму:
; 
.
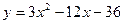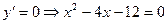Тоді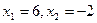 
- критичні точки.
Здобуті дані заносимо до таблиці.
| x | (-¥; -2) | -2 | (-2; 6) | (6; +¥) | |
| f¢(x) | + | - | + | ||
| f(x) | (зростає) | ¯ (спадає) | -175 | (зростає) |
Точка максимуму функцій М (-2; 81), точка мінімуму N (6; -175).
д) Точка перетину, інтервали опуклості та вгнутості:
y¢¢=6x-12, y¢¢=0, 6x-12=0 Þ x=2 – критична точка другого роду.
Дані заносимо до таблиці
| x | (-¥; 2) | (6; +¥) | |
| f¢¢ (x) | - | + | |
| f(x) | Ç (опукла) | -47 | È (вгнута) |
Точка перетину Е(2; -47).
е) Функція не має асимптот. Використовуючи здобуті данні, будуємо графік функції.
Рекомендована література
1. Барковський В.В., Барковська Н.В. Математика для економістів. Вища математика, - К.: Національна академія управління, 1997. – 397 с.
2. Высшая математика для экономистов. Учебное пособие для вузов/ Н. Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н. Фридман; под ред. Н.Ш. Кремера. – Банки и биржи, ЮНИТИ , 1997. – 439 с.
3. Глаголев А.А., Солнцева Т.В. Курс высшей математики. - М.: Высш. школа,1985.
4. Данко П.Е., Попов А.Г., Кожевныкова Т.Я. Высшая математика в упражнениях и задачах. В 2-х частях.: Учебное пособие для вузов. – Высш. школа, 1996.
5. Дубовик В.П., Юрик І.І. “Вища математика”. – К.: А.С.К., 2001.
6. Збірник задач з лінійної алгебри та аналітичної геометрії. – За ред. Рудавського Ю.К., Львів, “Бескид Біт”, 2002.
7. Кудрявцев В.А. Демидович В.П. Краткий курс высшей математики.. – М.: Наука, 1989.
8. Михайленко В.М. Федоренко Н.Д. Алгебра та геометрія для економістів: Учбовий посібник. – К.: УФІМБ, видавництво “Пошук”, 1997.
9. Рудавський Ю.К., Костробій П.П., Луник Х.П., Уханська Д.В. Математика для інженерів. Лінійна алгебра та аналітична геометрія. – Львів, “Бескид Біт”, 2002.